Afbeelding 1. Een zwart gat.Er valt van alles in een zwart gat – maar hoeveel informatie kan daarmee verdwijnen?
Entropie en de tweede wet van thermodynamica
Entropie is een maat voor de chaos die in een systeem heerst. Een chaotisch systeem heeft een hoge entropie, een geordend systeem een lage entropie. Een andere manier om het begrip entropie te beschrijven is als het gebrek aan informatie die we over het systeem hebben. Als we weinig over het systeem weten, dan is de entropie hoog, en als we er veel over weten, dan is de entropie laag.
Stel je, om deze beschrijvingen iets inzichtelijker te maken, een bak voor waar evenveel blauwe als witte ballen in zitten. Als de blauwe en witte ballen strikt gescheiden zijn – de blauwe bevinden zich bijvoorbeeld rechts en de witte links – en we pakken geblinddoekt een bal, dan zullen we doordat we ofwel links ofwel rechts reiken van te voren kunnen weten wat de kleur is van de bal die we eruit pakken. We spreken hier van een zeer geordend systeem, en het gebrek aan informatie is nihil omdat we precies weten waar de kleuren zich bevinden. De entropie is in dit geval nul. Zodra de ballenbak wordt geschud, zullen de blauwe en witte ballen willekeurig over de bak worden verdeeld. Het systeem is dan een stuk chaotischer, want de kennis over de uitkomst na een greep is onzeker. We hebben minder informatie over de exacte toestand van het systeem – we weten alleen dat er overal ongeveer evenveel blauwe als witte ballen zijn. De entropie is in dit geval groot. Entropie geeft dus aan hoe chaotisch het systeem is, of hoeveel informatie er over het systeem bekend is.
Een wonderlijke eigenschap van het begrip entropie is dat die grootheid altijd toeneemt of gelijk blijft. Het verschil in entropie tussen een begin- en een eindsituatie (∆S) is dus altijd gelijk aan of groter dan nul: ∆S ≥ 0. De chaos in ons universum neemt op den duur toe. Deze observatie – die uit de wetten van de statistiek bewezen kan worden – heet de tweede wet van de thermodynamica en is de reden dat sommige processen onomkeerbaar zijn. Als een druppel melk in een kop koffie valt, bijvoorbeeld, verspreiden de deeltjes zich over de vloeistof, maar ze zullen nooit weer dezelfde druppel vormen. Een ander voorbeeld: gebouwen storten wel vanzelf in, maar de stofwolken en het puin die daarbij geproduceerd worden, creëren niet weer vanzelf gebouwen. Beide zijn voorbeelden waar de tweede wet van thermodynamica aan ten grondslag ligt.
Afbeelding 2. Jacob Bekenstein.Afbeelding: met dank aan Yehonadav Bekenstein.
Entropie van zwarte gaten en de gegeneraliseerde tweede wet
In de jaren 70 realiseerde de Israëlische natuurkundige Jacob Bekenstein zich dat ook zwarte gaten een entropie moeten hebben. Bijzonder aan zwarte gaten is dat ze een horizon hebben. Het gedeelte achter de horizon is onzichtbaar voor waarnemers die zich ver buiten de horizon bevinden. Op het moment dat een object met een bepaalde entropie door het zwarte gat wordt opgeslokt, zou er daarom een bepaalde hoeveelheid entropie uit ons waarneembare universum verdwijnen. Maar dit betekent dat er sprake is van een netto afname van entropie, terwijl de tweede wet van thermodynamica stelt dat de entropie in ons universum enkel toe kan nemen! Een oplossing, voorgesteld door Bekenstein, is dat zwarte gaten ook een entropie zouden kunnen hebben – een die toeneemt op het moment dat er een object in verdwijnt. De tweede wet van thermodynamica zou dan uitgebreid moeten worden tot
ΔSBH + ΔS ≥ 0 (1)
waaris SBH de entropie van het zwarte gat is. Deze uitdrukking wordt de gegeneraliseerde tweede wet van de thermodynamica genoemd.
Maar wat is dan precies de definitie van de entropie van een zwart gat? Een observatie van Roger Penrose en R.M. Floyd in 1971 was dat de oppervlakte van de horizon van een zwart gat onder iedere mogelijke verandering toeneemt – een zwart gat kan immers alleen maar groeien – iets wat je wellicht doet denken aan de tweede wet van thermodynamica. Bovendien schermt de horizon informatie over het binnenste van het zwarte gat af, waardoor een waarnemer buiten het zwarte gat onwetend is over de interne toestand, iets wat opnieuw doet denken aan entropie. Bekenstein stelde daarom voor dat de entropie van het zwarte gat, SBH, evenredig is met de oppervlakte van de horizon . Na wat finetuning van de evenredigheidsconstante door Stephen Hawking[1], werd de formule voor de entropie van zwarte gaten uiteindelijk
SBH = A/(4G) (2)
In deze formule, die ook wel de Bekenstein-Hawkingformule wordt genoemd, is G de zwaartekrachtsconstante van Newton.
Door entropie van zwarte gaten te definiëren, voorkwam Bekenstein dat de tweede wet van de thermodynamica geschonden kan worden. Maar hij realiseerde zich al gauw dat de gegeneraliseerde tweede wet van de thermodynamica een begrenzing met zich meebrengt. Als de entropie van een object dat in een zwart gat verdwijnt, ΔS, groter is dan de toename in de entropie van het zwarte gat onder dit proces, ΔSBH, is formule (1) niet meer geldig. Daarom stelde Bekenstein dat de entropie van normale objecten nooit groter kan zijn dan de verandering in de entropie van een zwart gat die zo’n object veroorzaakt op het moment dat het in het zwarte gat valt. In formulevorm:
ΔS ≤ ΔSBH (3)
Om beter te begrijpen wat deze ongelijkheid precies betekent, helpt het om de vergelijking volledig te beschrijven in termen van eigenschappen van normale objecten, en dit is wat Bekenstein met behulp van een gedachte-experiment deed.
Gedachte-experiment
Beeld je de volgende situatie in: een zwart gat en een waarnemer die zich daar heel ver vandaan bevindt. De waarnemer houdt een heel dun draadje vast waaraan een doos vastzit. De doos heeft een grootte R, een entropie Sdoos, en een energie Edoos = 2πν, waar ν de frequentie is. (De laatste vergelijking is de bekende wet van Planck die energieën en frequenties met elkaar verbindt, maar dan geschreven in slimme eenheden waarin de constante van Planck 2π is.) Stel je nu voor dat de waarnemer de doos heel langzaam naar het zwarte gat toe laat glijden – zo langzaam, dat er geen energie in kinetische energie wordt omgezet.
Als de doos dicht bij het zwarte gat in de buurt komt, gaat gravitationele roodverschuiving een rol spelen. Dit is een effect dat erg op het Dopplereffect lijkt: als bijvoorbeeld een politieauto naar je toekomt wordt de geluidsgolf als het ware samengedrukt waardoor het geluid hoger klinkt. Als de auto weer van je vandaan rijdt, worden de geluidsgolven uitgerekt waardoor het geluid juist lager klinkt. Voor lichtgolven heb je een soortgelijk principe: als een lichtgolf wordt samengedrukt en daarmee de frequentie hoger wordt, verschuift het licht dat je ziet naar de blauwe kant van het spectrum: blauwverschuiving. Andersom: als een lichtgolf wordt uitgerekt, dan wordt de frequentie lager en verschuift het licht naar het rode eind van het spectrum: roodverschuiving. Op het moment dat onze doos zich vlakbij de horizon van het zwarte gat bevindt, waar sprake is van een sterk zwaartekrachtsveld, wordt de golf die de energie van de inhoud bepaalt ook uitgerekt en vindt er roodverschuiving plaats. Een intuïtieve manier om je dit voor te stellen, is door te beseffen dat zware objecten de ruimte-tijd krommen. Afstanden worden hierdoor groter, waardoor de golven over een grotere ruimte worden uitgespreid en er dus (gravitationele) roodverschuiving plaatsvindt.
Voor de waarnemer die zich ver van het zwarte gat bevindt, vindt er dus een roodverschuiving in het energiespectrum van de doos plaats. Deze waarnemer ziet hierdoor een afname van energie. Het draadje dat tussen de doos en de waarnemer is gespannen, is de enige verbinding met de buitenwereld waardoor die energie kan verdwijnen, en dus “stroomt de energie door het draadje” en bereikt de waarnemer als arbeid. Vanuit het perspectief van het zwarte gat echter neemt zijn energie juist toe op het moment dat de doos erin valt. Behoud van energie impliceert dat de hoeveelheid arbeid die het zwarte gat op de waarnemer uitoefent en de toename in energie van het zwarte gat zelf aan elkaar gelijk moeten zijn. Anders gezegd: twee verschillende waarnemers, één in het zwarte gat en één ver daarbuiten, kijken anders naar dezelfde gebeurtenis. Het is daarom mogelijk dat zij een andere uitdrukking vinden voor, in dit geval, het energieverschil dat er door die gebeurtenis optreedt. Maar uiteindelijk blijven beide waarnemers natuurlijk dezelfde gebeurtenis beschrijven, en dus moeten de uitdrukkingen die voor het energieverschil worden gevonden aan elkaar gelijk worden gesteld. Zoals we zullen zien, is het op deze manier mogelijk om vergelijking (3) volledig in eigenschappen van de doos te vatten.
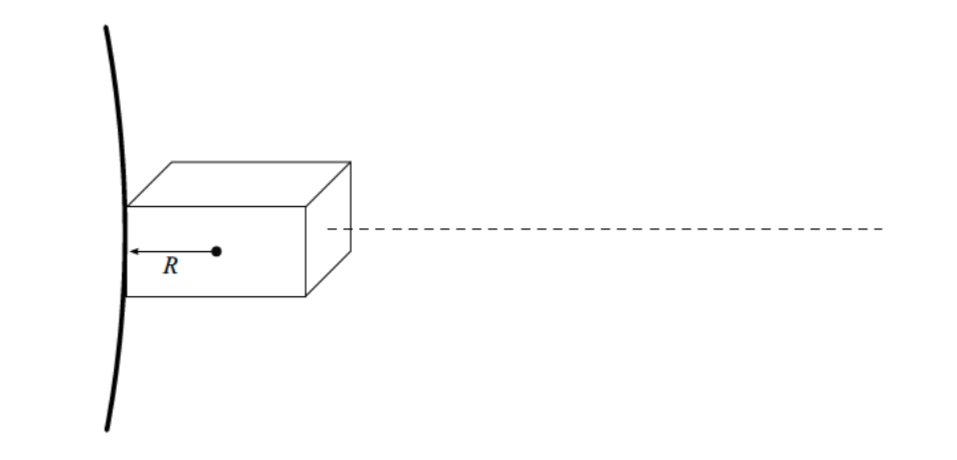
Afbeelding 3. Bekensteins gedachte-experiment.Een doos van grootte R die zich vlak bij de rand van een zwart gat bevindt.
Stel je voor dat de situatie is zoals in afbeelding 3 – de doos bevindt zich met zijn rand precies tegen de horizon van het zwarte gat, en de doos valt er vanaf dit punt in. Dan vindt er vanuit het perspectief van de waarnemer op afstand een oneindige roodverschuiving plaats en verliest de doos dus ál zijn energie. De arbeid die de waarnemer onder deze gebeurtenis via het draad ontvangt, is
ΔW = F Δx = a Edoos R (4)
Het eerste isgelijkteken is niets anders dan de definitie van wat arbeid is; bij het tweede gebruiken we dat F = ma = a Edoos/c2 (met Einsteins beroemde formule E = mc2). In formule (4) hebben we bovendien eenheden gekozen waarin c, de snelheid van het licht, gelijk is aan 1. De versnelling a is in deze vergelijking een gravitationele versnelling. De gravitationele versnelling geeft aan hoe sterk het zwarte gat aan de doos trekt – net zoals we hier op aarde bijvoorbeeld een gravitationele versnelling van g = 9.81 m/s2 hebben.
Vanuit het perspectief van het zwarte gat vindt er een energietoename plaats op het moment dat de doos erin valt. De berekening van deze energietoename kunnen we doen met een thermodynamische wet die ons vertelt dat de energietoename gelijk is aan de temperatuur maal de entropietoename. Volgens Einstein is energietoename weer hetzelfde als massatoename, dus uiteindelijk is het mogelijk om de massaverandering van het zwarte gat, ΔM, die het ondergaat doordat de doos erin valt, te relateren aan de verandering in entropie die het door deze transformatie ondergaat:
ΔM = T ΔSBH (5)
Hierin is T de temperatuur van het zwarte gat. Door de arbeid die de waarnemer via het draad ontvangt en het massaverschil dat het zwarte gat ondergaat als de doos erin valt gelijk te stellen, zoals we hierboven beschreven, vinden we
ΔSBH = a Edoos R / T = 2 π Edoos R (6)
In de laatste stap hebben we de formule voor de temperatuur in een zwaartekrachtsveld – de zogeheten Unruhtemperatuur, T = a / (2π), ingevuld. Als we nu vergelijking (6) in ongelijkheid (3) invullen, vinden we onze einduitdrukking:
ΔS ≤ 2 π Edoos R
Dit is de Bekenstein bound: de entropie van een object of een fysisch systeem kan nooit groter zijn dan het product van zijn energie en grootte.
Een mooi resultaat, maar wat hebben we hier nu aan? De grens van Bekenstein speelt een heel belangrijke rol in de studie van de quantumzwaartekracht, maar is ook van belang bij meer “aardse” processen. Door de relatie tussen entropie en informatie wordt bijvoorbeeld vaak gesuggereerd dat de grens verstrekkende gevolgen voor computers heeft: omdat een computer een systeem is van eindige energie en eindige grootte, zou de Bekenstein bound betekenen dat een onbegrensd computergeheugen onmogelijk is. De bovenstaande redenering maakt natuurlijk gebruik van nogal wat exotische natuurkunde – quantummechanica én relativiteitstheorie, bijvoorbeeld; twee theorieën die we nog niet goed hebben kunnen samenvoegen. Of Bekensteins grens dus helemaal waterdicht is zal de toekomst moeten leren, maar vooralsnog lijkt het erop dat die grens ons veel kan vertellen over natuurkunde op de allerfundamenteelste schaal.
Referenties
J. D. Bekenstein, “Black holes and entropy,” (1973)
R. Penrose and R. M. Floyd, “Extraction of rotational energy from a black hole,” (1971)
[1] Bekenstein stelde aanvankelijk een voorfactor van 1/8pi ln(2) voor. Stephen Hawking stelde dit een jaar later bij tot een waarde van ¼.
