
Als je pi (of het Griekse symbool ervoor, π) in je rekenmachine invoert krijg je 3,1415926535… – een uitkomst die simpelweg het getal pi uitgedrukt is in ons tientallige stelsel. Het is bekend dat pi een irrationaal getal is, wat wil zeggen dat het niet te schrijven is als een breuk, dus niet als verhouding van twee gehele getallen. Dat betekent ook dat de decimalen die na de komma volgen nooit een herhalend patroon zullen vertonen. Er is dus maar één manier om erachter te komen wat de eerste – laten we zeggen duizend – decimalen zijn: ze gewoonweg berekenen. Maar ja, hoe doe je dat eigenlijk?
De meest ouderwetse – en ook meest intuïtieve – manier om pi te berekenen is door polygonen (veelhoeken) in en rondom de cirkel te leggen en die steeds meer hoeken te geven zodat ze de gladheid van een echte cirkel benaderen. Een alternatieve manier die ik hier wil uitlichten is aan de hand van het binomium van Newton.
Het was lang geleden, in de 17de eeuw, dat Isaac Newton polynomen van de vorm \( (1+x)^n \) bestudeerde. Hij was geïnteresseerd in het expanderen van deze machten, wat leidt tot de volgende uitdrukkingen:
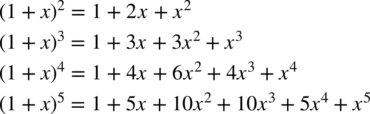
Deze getallen die je aan de rechterzijde krijgt, kun je makkelijk voorspellen door middel van de driehoek van Pascal. Sterker nog, voor een generieke macht n bestaat de volgende formule:
\( (1+x)^n = 1+ n x + \frac{n(n-1)}{1!} x^2 + \frac{n(n-1)(n-2)}{2!} x^3+ …. \).
De rechterzijde gaat door totdat je in de breuk \( n(n-1)(n-2)….(n-n) = 0 \) bereikt en de reeks ophoudt te bestaan. Deze ingewikkelde breuken – die overigens steeds gehele getallen opleveren! – zijn precies de getallen die in de driehoek van Pascal voorkomen. Ze heten ook wel binomiaalcoëfficiënten en worden vaak geschreven als
![]()
Hierboven zien we dus dat de binomiaalcoëfficiënten verschijnen als we \( (1+x)^n \) expanderen, waarbij n een positief geheel getal is:
![]()
De uitdrukking hierboven is ook wel bekend als het binomiaaltheorema of binomium van Newton.
Newton stelde vervolgens zichzelf de vraag: wat als we nu aannemen dat n niet een positief maar negatief getal is of zelfs een breuk; werkt de bovenstaande formule dan nog? Het blijkt dat we in dat geval nog steeds de binomiaalcoëfficiënten kunnen gebruiken, alleen is het bijzondere nu dat de rechterzijde van de expansie een oneindige reeks wordt! We bereiken namelijk nooit het punt waarop in de binomiaalcoëfficiënt nul wordt: er komt geen factor \( (n-n) \) in de coëfficiënt voor. In het geval dat n=-1 vinden we bijvoorbeeld de bekende meetkundige reeks voor \( -x \):
\( \frac{1}{1+x} = 1-x+x^2-x^3+x^4-x^5+ … \).
De reeks blijkt te kloppen als x tussen de 1 en -1 ligt, zoals je zelf kunt nagaan. Ook als n een breuk is, kun je de formule gebruiken. In dat geval vind je wederom een oneindige reeks, zoals bijvoorbeeld bij n = ½:
\( (1+x)^{1/2} = 1+\frac{1}{2}x-\frac{1}{8}x^2 + \frac{1}{16}x^3-\frac{5}{128}x^4+ … \).
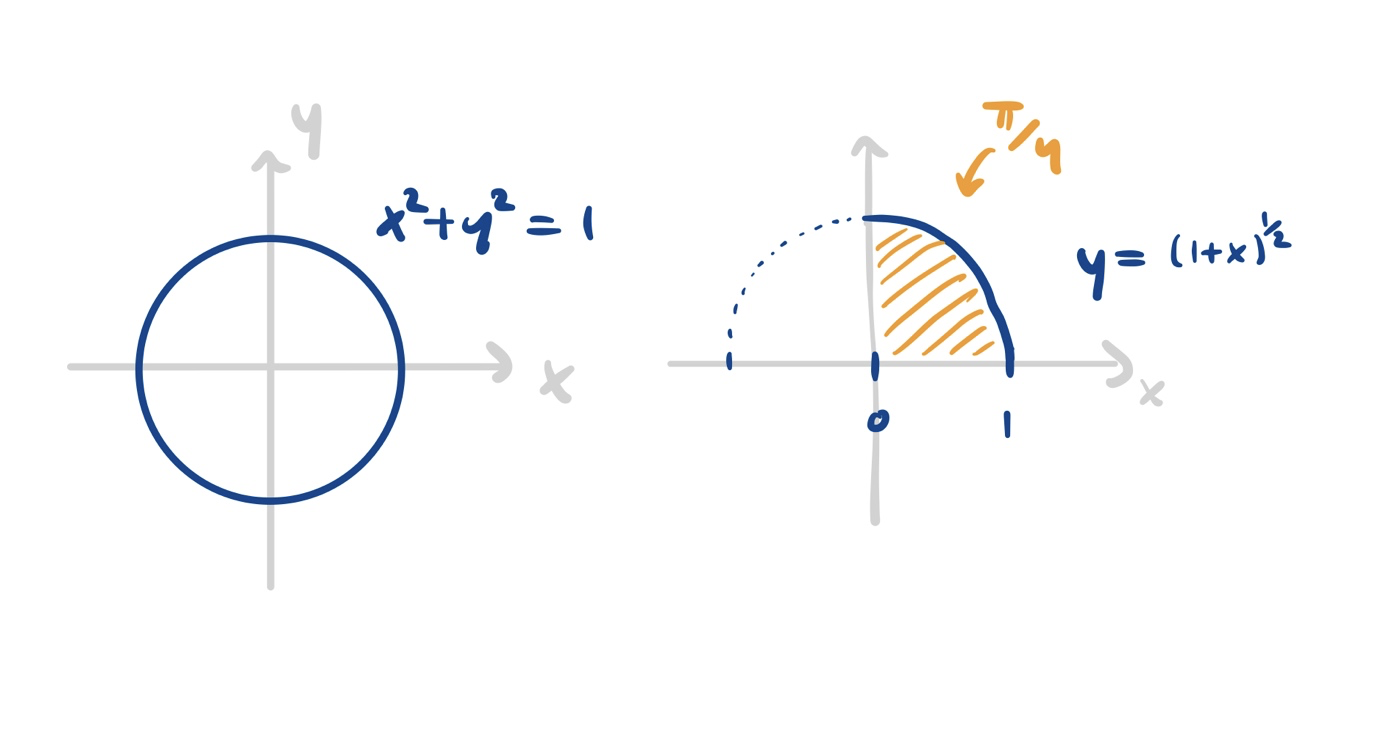
Het interessante nu is dat Newton inzag dat deze laatste reeks gebruikt kan worden om het getal pi tot hoge precisie uit te rekenen. Dat deed hij als volgt: de eenheidscirkel in een grafiek wordt beschreven door de formule
\( x^2+y^2 = 1 \).
Deze formule kun je omschrijven zodat je y in termen van x kunt uitdrukken. Wat je dan vindt is:
\( y = \sqrt(1-x^2) \).
Wat Newton opmerkte is dat, als we deze functie integreren van 0 tot 1, we een kwart van de oppervlakte van een cirkel berekenen – zie ook de afbeelding hieronder. Oftewel:
\( \frac{\pi}{4} = \int_0^1 \sqrt(1-x^2) \).
Nu kunnen we onze binomiaalcoëfficiënten gebruiken. Als we in originele formule x door -x2 vervangen, dan vinden we
\( \frac{\pi}{4} = \int_0^1 \left(1-\frac{1}{2}x^2-\frac{1}{8}x^4-\frac{1}{16}x^6-\frac{5}{128}x^8 – … \right) dx = 1-\frac{1}{6}-\frac{1}{40}-\frac{1}{112} -\frac{5}{1152} + … \).
Zo kunnen we eenvoudig tot op willekeurige precisie de decimalen van pi berekenen! We zien dus dat het binomium van Newton, dat op het eerste gezicht niets met cirkels te maken lijkt te hebben, wel degelijk gebruikt kan worden om het getal pi met veel precisie te bepalen.
Als je in meer detail wilt weten hoe dit werkt, of wilt zien hoe deze methode zelfs nog verder versneld kan worden, dan raad ik je aan onderstaande video van het YouTubekanaal Veritasium te bekijken!