
Negatieve getallen in de natuur.We komen in de natuur vaak negatieve getallen tegen – bijvoorbeeld op de thermometer. Maar wat zijn negatieve getallen nu precies? Afbeelding: Antti T. Nissinen.
Je hebt nog vier euro in je portemonnee, en je wilt een broodje van zeven euro kopen. Hoeveel geld houd je over? De vraag lijkt onzinnig: je hebt immers niet genoeg geld om het broodje te kunnen kopen. Toch is duidelijk dat het getal ‘drie’ in het vraagstuk een rol speelt: je komt immers precies drie euro tekort. Diezelfde drie euro zou je tekortkomen als je twee euro in je portemonnee had en broodje van vijf euro wilde kopen – in zekere zin is het antwoord op die tweede vraag dus precies hetzelfde. Maar als je acht euro in je portemonnee hebt en het broodje kost negen euro, dan is het antwoord anders: dan kom je immers maar één euro tekort.
Negatieve getallen
Het moge duidelijk zijn welk begrip we nodig hebben om de bovenstaande drie vragen te kunnen categoriseren: dat van negatieve getallen. Vier euro min zeven euro is ‘min drie euro’, en twee euro min vijf euro is ook ‘min drie euro’: door de twee getallen van elkaar af te trekken, en ons er niets van aan te trekken dat we daarbij onder nul uitkomen, kunnen we inzien dat onze eerste twee vraagstukken tot hetzelfde antwoord leiden, maar het derde vraagstuk – acht euro min negen euro is min één euro – tot een ander antwoord.
Tellen is iets wat mensen waarschijnlijk al sinds het begin der tijden doen. Hoeveel appels hangen er aan deze boom? Hoeveel runderen staan er in die kudde? Ook optellen en aftrekken zijn heel natuurlijke bewerkingen: als onze stam uit zeventien leden bestaat en er worden drie kinderen geboren, hoeveel monden moeten we dan voeden? En wat als er twee ouderen overlijden?
Of het begrip van negatieve getallen al net zo oud is valt te betwijfelen. In een stam van zeventien leden zullen er nooit dertig overlijden, en van een boom met tien appels zul je er geen vijftien plukken. Begrippen als ‘min dertien’ en ‘min vijf’ zijn minder hard nodig om te overleven dan ‘twee’ en ‘zeven’. In historische documenten komen we negatieve getallen dan ook pas tegen rond het begin van onze jaartelling, in een Chinees document dat vrij vertaald Negen hoofdstukken over de kunst van de wiskunde heet. In de derde eeuw, ook in China, wordt ook duidelijk beschreven hoe je met zulke negatieve getallen rekent: hoe je ze bij elkaar optelt en zelfs van elkaar aftrekt.
Een nette definitie
Hoe kunnen we nu wiskundig precies maken wat negatieve getallen zijn? Stel dat we leven in een wereld waarin alleen positieve getallen bekend zijn. Laten we zeggen dat we daarmee alle gehele getallen vanaf 1 bedoelen – ook het getal nul is een begrip dat niet altijd bekend is geweest. Hoe maken we aan onze mede-wiskundigen duidelijk wat we bedoelen met negatieve getallen en met nul? In onze uitleg zal in elk geval moeten blijken dat de eerste twee rekenvoorbeelden hierboven – vier min zeven en twee min vijf – leiden tot hetzelfde negatieve getal, maar dat acht min negen leidt tot een ander negatief getal.
Dat leidt ons tot het volgende idee: laten we alle paren van gewone, positieve getallen eens in een nette tabel schrijven:
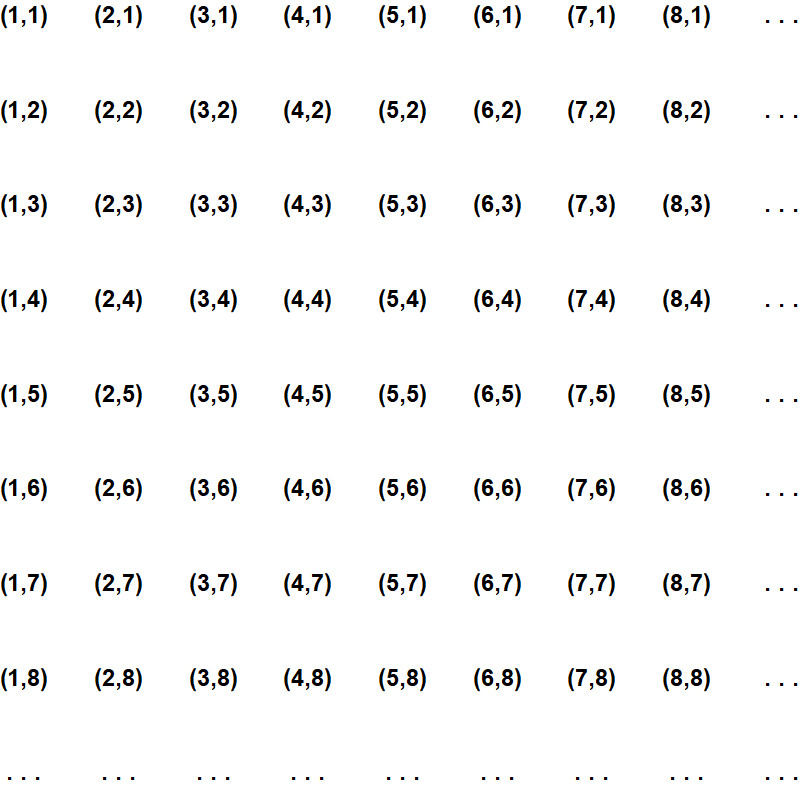
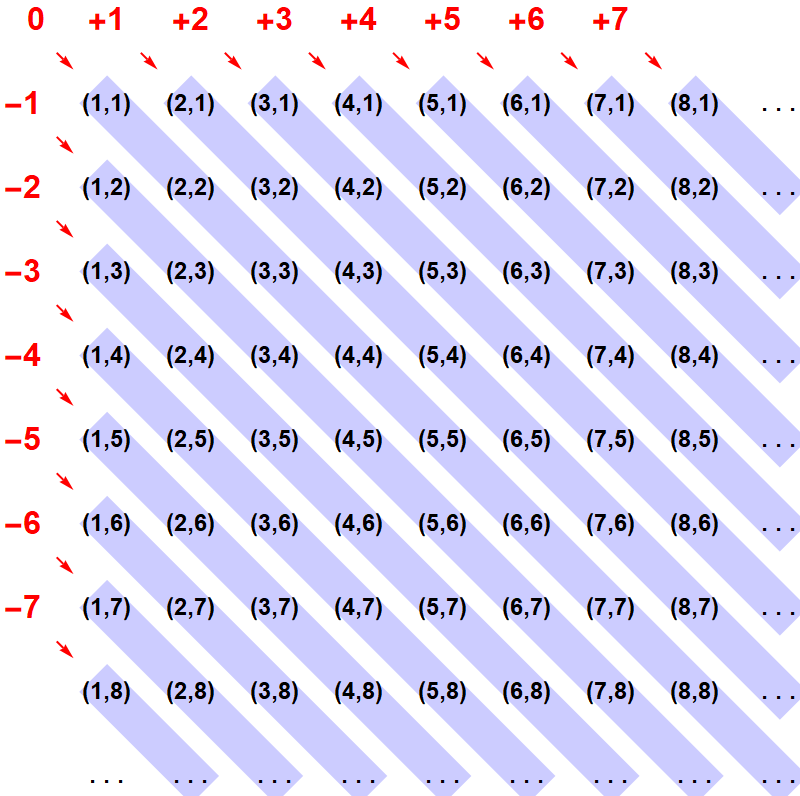
In deze tabel zien we bijvoorbeeld (2,5) staan, en deze combinatie willen we nu zien als het antwoord op de rekensom ‘twee min vijf’. (2,5) staat dus voor ‘drie tekort’, oftewel: voor min drie. Maar (2,5) is natuurlijk niet de enige combinatie die daarvoor staat: zoals we al hebben gezien betekent (4,7) ook ‘drie tekort’, en dat geldt natuurlijk ook voor (1,4), voor (3,6), enzovoort. Kortom: we willen de hele diagonaal waarop al deze paren in de tabel staan, zien als weergaven van ‘het getal min drie’. We willen onze getallencombinaties dus in groepen rangschikken, zoals in de tabel hieronder:

Elke groep, aangegeven met een blauwe band, staat nu dus voor één getal: de groep waarin (2,5) voorkomt staat voor ‘min drie’, en de groep waarin (4,2) voorkomt staat voor ‘plus twee’. In onze constructie komen nu alle getallen, positief én negatief, voor:
Nooit meer minnen
De bovenstaande constructie lijkt nogal gecompliceerd voor het invoeren een begrip wat voor ons gevoel betrekkelijk eenvoudig is. Het idee heeft echter een heel groot voordeel: in deze constructie hebben we het begrip ‘min’ nooit meer nodig! Laten we bijvoorbeeld eens kijken naar de vraag ‘wanneer zitten twee paren in dezelfde groep?’
De paren (2,5) en (4,7) staan bijvoorbeeld allebei in de groep ‘min drie’. Waarom? Omdat 2-5 hetzelfde is als 4-7, natuurlijk. Die oplossing is in zekere zin valsspelen, want 2-5 en 4-7 zijn nou juist de nieuwe begrippen die we willen definiëren… Maar wacht eens: we kunnen
2-5=4-7
ook omschrijven tot
2+7=4+5
In die beschrijving komen alleen positieve getallen en plustekens voor! En dit geldt algemeen: de paren (a,b) en (c,d) behoren tot dezelfde groep zodra a+d gelijk is aan b+c – probeer het zelf maar uit voor een paar voorbeelden. We hebben daarmee een test die ons vertelt of twee paren hetzelfde negatieve getal beschrijven – een test die zelf alleen gebruik maakt van positieve getallen en optellen!
Iets soortgelijks kunnen we doen met wiskundige bewerkingen. Wat is bijvoorbeeld het antwoord als we (2,5) willen optellen bij (4,2)? In gewone woorden: wat krijgen we als we ‘min drie’ optellen bij ‘plus twee’? Het antwoord zou natuurlijk ‘min één’ moeten zijn, en dat kun je krijgen door de losse componenten van de paren op te tellen:
(2,5) + (4,2) = (2+4, 5+2) = (6,7)
Het antwoord behoort inderdaad tot de groep ‘min één’. En merk weer op: nergens in deze berekening gebruiken we een negatief getal of een minteken!
Tenslotte: hoe rekenen we ‘twee’ min ‘min drie’ uit? Het antwoord zou natuurlijk ‘vijf’ moeten zijn. Hoe krijgen we dat uit bijvoorbeeld de paren (4,2) en (2,5)? Wie wat puzzelt vindt het antwoord:
(4,2) – (2,5) = (4+5,2+2) = (9,4)
Oftewel: om (2,5) ergens van af te trekken draaien we simpelweg de volgorde om (dat komt immers overeen met een minteken) en tellen vervolgens (5,2) bij ons eerste getal op. Algemener:
(a,b) – (c,d) = (a+d,b+c)
en in de berekening rechts hebben we wederom alleen positieve getallen en plustekens nodig.
We hebben in onze constructie dus niet alleen negatieve getallen ‘gemaakt’; we kunnen nu ook met zulke getallen (en onze oude vertrouwde positieve getallen én het getal nul) rekenen zonder ooit een minteken nodig te hebben!
…ja, en dus?
Een leuke wiskundige truc natuurlijk, maar wat hebben we hier nu aan? Het was de wiskundige Alexander Grothendieck die dat in de jaren 50 van de vorige eeuw besefte. De bovenstaande constructie kun je namelijk niet alleen toepassen op getallen, maar op álles waarvoor iets als ‘optellen’ is gedefinieerd. Denk bijvoorbeeld aan een ronde schijf die je alleen maar met de klok mee kunt draaien. Je kunt zulke draaiingen ook ‘optellen’ door ze achter elkaar uit te voeren: eerst een draaiing over 40 graden, dan een draaiing over 30 graden, maakt samen een draaiing over 70 graden. Met precies dezelfde constructie als hierboven kun je nu ook draaiingen tegen de klok in beschrijven: een draaiing over 30 graden ‘min’ een draaiing over 40 graden is een draaiing over 10 graden tegen de klok in.
Nog een wat gecompliceerder voorbeeld voor de liefhebbers: we gaan weer terug naar de positieve gehele getallen, maar vervangen ‘optellen’ nu door ‘vermenigvuldigen’. Met de bovenstaande constructie kunnen we nu delen definiëren: (2,3) betekent in dat geval de breuk 2/3, en nu willen we (2,3) in dezelfde groep plaatsen als bijvoorbeeld (4,6) omdat 4/6 gelijk is aan 2/3. We kunnen dat weer schrijven als 4 x 3 = 2 x 6, dus algemener: (a,b) zit in dezelfde groep als (c,d) wanneer a x d gelijk is aan b x c. Wie dit voorbeeld bestudeert, op dezelfde manier als het geval van de negatieve getallen hierboven, zal zien dat we op deze manier uit de positieve gehele getallen alle positieve breuken kunnen construeren, en dat we – nu met alleen maar vermenigvuldigen – ook het delen van zulke breuken kunnen beschrijven.
De algemene vorm van de constructie die ik in dit artikel aan de hand van negatieve getallen heb uitgelegd, is vernoemd naar Grothendieck: de structuur die we krijgen heet een Grothendieck-groep. Het idee is steeds hetzelfde: begin met een operatie die je maar in één richting kunt uitvoeren, en eindig met iets waarin je beide kanten op kunt: van optellen naar optellen én aftrekken, van vermenigvuldigen naar vermenigvuldigen én delen, enzovoort. Maar wat heeft die structuur nu met natuurkunde te maken? Het blijkt dat Grothendieck-groepen ook op diverse plaatsen in de natuurkunde voorkomen – bijvoorbeeld in de snaartheorie, als we snaarvormige en hogerdimensionale deeltjes willen beschrijven en classificeren. We moeten Grothendiecks constructie dan niet toepassen op getallen maar op vectorbundels. Wat dat zijn leg ik uit in deel twee van dit drieluik, dat op 16 augustus verschijnt. In deel 3 gaan plakken we vervolgens de ideeën uit de twee artikelen aan elkaar, en zullen we zien hoe iets wat begint als ‘wiskundig muggenziften’ uiteindelijk leidt tot allerlei interessante lessen over de natuurkunde.