Afbeelding 1. Fibonaccigetallen in de natuur.De Fibonaccigetallen komen veel voor in de natuur – de verhoudingen van achtereenvolgende lengtes en breedtes van deze spiraal in een cactus zijn bijvoorbeeld vrijwel gelijk aan de Fibonaccigetallen. Maar gek genoeg kunnen de Fibonaccigetallen niet voorkomen als energieën in een quantummechanisch systeem! Hoe zit dat met andere getalreeksen – de priemgetallen, bijvoorbeeld? Foto: Brewbooks.
De Schrödingervergelijking en waterstof
De Schrödingervergelijking is het onbetwiste paradepaardje van de quantummechanica. Deze formule voorspelt wat de mogelijke energieën van quantummechanische golven zijn, op basis van hoe de potentiële energie varieert door de ruimte. De wiskundige functie die vertelt hoe die potentiële energie verandert in de ruimte, heet de potentiaal.
Laten we eens een voorbeeld van de Schrödingervergelijking in actie bekijken. Stel dat je wilt weten wat de mogelijke energieën zijn die elektronen in een waterstofatoom kunnen hebben. Je hebt daarvoor dus in de eerste plaats de Schrödingervergelijking nodig, en daarnaast de potentiaal van een waterstofatoom. Gelukkig weet je dat de kern van een waterstofatoom een proton is, met een precieze lading, en dat blijkt voldoende zijn om de potentiaal uit te rekenen. Het antwoord staat bekend als de wet van Coulomb:
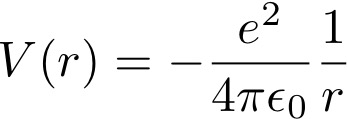
In deze formule staat V(r) voor de potentiaal. Die is afhankelijk van de afstand van het elektron tot het proton, r. Verder staat e voor de elementaire ladingseenheid en ε0 voor de zogeheten diëlektrische constante van het vacuüm.
Potentialen en getallen
Vul de Coulombpotentiaal in de Schrödingervergelijking in, en na het nodige rekenwerk krijg je al spoedig voorspellingen over energieën van elektronen in het waterstofatoom. Over het algemeen geeft de Schrödingervergelijking een reeks aan energieën,
![]()
die in oplopende volgorde gelabeld kunnen worden een geheel getal n, het energieniveau. Voor het specifieke geval van het waterstofatoom zijn de energieën gegeven door
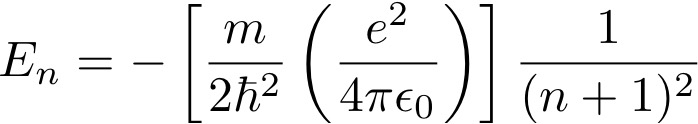
Hier is m de massa van het elektron en ħ een quantummechanische natuurconstante die bekend staat als de gereduceerde constante van Planck.
In het algemeen kunnen de energieën de meest uiteenlopende waarden aannemen, afhankelijk van de potentiaal die je kiest. Een interessante wiskundige vraag is: kun je elke getallenreeks nabootsen als een reeks van energieën door maar een juiste, gekunstelde potentiaal te kiezen? Het antwoord luidt: nee. Betekent dit dat er ook geen potentiaal is die alle priemgetallen produceert als bijbehorende energieën? Niet per se…
Getalreeksen: Fibonacci
Er bestaat bijvoorbeeld wél een potentiaal waarmee je als energieënreeks de reeks van oneven getallen kan krijgen:
![]()
De potentiaal die hiervoor nodig is ziet eruit als een parabool.
Voor we ons wagen aan de reeks van priemgetallen, vragen we ons af of er ook een potentiaal bestaat die de Fibonaccireeks als energieën geeft. Een deel van de Fibonaccireeks is
![]()
Deze reeks is als volgt gedefinieerd: elk Fibonaccigetal kan worden berekend door de twee voorgaande getallen op te tellen. Begin dus met 1, 1, 2, 3, 5, … en je zult al snel bij de bovenstaande waarden uitkomen.
Het blijkt niet mogelijk te zijn om een potentiaal te verzinnen die de Fibonaccireeks als energieën reproduceert. De reden daarvoor blijkt te zijn dat de Fibonaccireeks te sterk groeit wanneer n groter wordt. Een analyse toont aan dat een reeks maximaal zo snel als n2 mag groeien om beschreven te kunnen worden door een quantummechanische potentiaal. Die groeis is iets dat de Fibonaccireeks al snel overtreedt: bij n=12 is het getal in de reeks hierboven bijvoorbeeld al gelijk aan n2=144, en daarna groeit de reeks alleen maar sneller.
Priemgetallen
Tot slot bekijken we de reeks van priemgetallen,
![]()
Groeit deze reeks traag genoeg om in principe een bijbehorende potentiaal te hebben? Ja! Het is namelijk zo dat priemgetallen ongeveer zo snel groeien als n log(n), met een afwijking van maximaal 10%. Die groei is minder sterk dan een kwadratische groei: het n-de priemgetal is altijd (veel) kleiner dan n2.
Het zou dus zo kúnnen zijn dat er een potentiaal bestaat die als energieën alleen alle priemgetallen toestaat. Stel nu dat je een experimentele opzet kan verzinnen die ook echt deze hypothetische potentiaal heeft. Dan zou je getallen kunnen testen op de priemeigenschap door te meten of de bijbehorende energie in het systeem voorkomt, of niet – en dat kunnen we vrij eenvoudig meten. Op deze wijze ontwijk je dus ontzettend veel rekentijd met computers.
Maar goed, eerst moet men maar eens deze potentiaal ontdekken… Dat is nog altijd niet gelukt, en is ook beslist niet eenvoudig, maar er wordt wel degelijk onderzoek gedaan naar dit wat exotische maar erg interessante vraagstuk.
Nieuwsgierig geworden? Veel meer over dit verrassende verband tussen reeksen van (priem-) getallen en de quantummechanica vind je in dit (wetenschappelijke) artikel:
