
Afbeelding 1. Quantummecanica: raar of niet?Veel mysterieus klinkende eigenschappen van de quantummechanica zijn eiggenlijk niet vreemder dan de eigenschappen van watergolven. Foto: Roger McLassus.
Sterker nog, verreweg de meeste dingen in de quantumtheorie waarvan je in eerste instantie zou denken dat ze niets met de wereld van alledag te maken hebben, blijken helemaal niet speciaal quantummechanisch te zijn. Je kunt precies dezelfde effecten ook tegenkomen in de badkuip thuis, tijdens een wandeling aan het strand, of rustig varend door een kanaal. In situaties dus, die niets met quantumtheorie of quantumdeeltjes van doen hebben.
Dat wil natuurlijk niet zeggen dat de quantumtheorie helemaal niets speciaals heeft toe te voegen aan de meer doorsnee natuurkunde. Er zijn wel degelijk dingen die echt alleen in de quantumwereld kunnen, en het zijn natuurlijk juist die dingen die quantummechanica zo spannend en krachtig maken. Maar welke dingen nu precies raar en echt quantum zijn, en welke dingen eigenlijk niet, is wellicht niet zoals je het op het eerste gezicht zou verwachten. Dit artikel legt daarom eerst bij een aantal van de vreemdst klinkende quantumeffecten uit waarom die eigenlijk heel normaal zijn, en laat daarna zien wat voor dingen quantumdeeltjes kunnen doen die echt speciaal en anders zijn.
Golven
Voor we beginnen met het bestuderen van raar quantumgedrag, moeten we eerst één lest van de quantummechanica goed in ons door laten dringen:
Puntdeeltjes bestaan niet — alles bestaat uit golven
Deze realisatie is de grondslag, en het allerbelangrijkste ingrediënt, van de quantumtheorie. Maar wat bedoelen we hier eigenlijk met deeltjes en golven? Zoals je waarschijnlijk wel weet beschrijven de wetten van Newton hoe je door het uitoefenen van een kracht een massa aan het bewegen kan brengen. De massa’s waar we het dan over hebben zijn vaak dingen zoals biljartballen, planeten en knikkers. Grote objecten dus, met een massa, een positie en een snelheid. Een dergelijke beschrijving van de natuur gaat ook voor kleinere objecten nog heel lang goed. Om de Lorentzkracht uit te rekenen die een elektrische stroom ondervindt in een magnetisch veld, kunnen we bijvoorbeeld aannemen dat de stroom bestaat uit een serie heel kleine bolletjes die allemaal een kleine elektrische lading hebben. Je zou daardoor verleid kunnen worden om je atomen en elektronen voor te stellen als om elkaar heen draaiende miniatuurplaneetjes, die allemaal zo klein zijn als een enkel punt in de ruimte. Dat beeld van de kleinste deeltjes in de natuur is echter fundamenteel fout.
De centrale les van de quantummechanica is dat microscopische deeltjes eigenlijk helemaal geen deeltjes zijn. Dat wil zeggen, het zijn geen puntdeeltjes of miniatuur-planeetjes. Het blijkt veel beter te zijn om over dingen als elektronen en atomen na te denken in termen van golven. Golven kennen we natuurlijk allemaal. Als je een steen in een stilstaand meer gooit, krijg je cirkelvormige golven die zich verspreiden over het wateroppervlak. Op zee creëert de wind lange, rechte golven die met witte koppen het strand op rollen. Dit zijn allebei golven op een tweedimensionaal oppervlak. We kennen echter ook golven in drie dimensies. Geluid, bijvoorbeeld, bestaat uit trillingen in de lucht. Als je de bastonen van je favoriete muziek wat versterkt, kun je die trillingen zelfs letterlijk voelen. Elektronen en andere quantumdeeltjes zijn vergelijkbaar met precies zulk soort golven. Het zijn uitgespreide trillingen in de driedimensionale ruimte.
Natuurlijk vraag je je nu meteen af wàt er dan precies aan het trillen is als er een elektron voorbijkomt. Het enigszins teleurstellende antwoord is: een onzichtbaar quantumveld. Je kunt quantumvelden een beetje vergelijken met de lucht in een kamer. De lucht is door de hele kamer verspreid, maar je ziet er niets van. Alleen de trillingen van de lucht, dat wil zeggen: geluid, kun je opmerken. Op dezelfde manier zit het heelal vol met een quantumveld waar we niets van merken. Alleen de trillingen van het veld kunnen we waarnemen, want dat zijn dingen als elektronen en atomen. Maar let op: de vergelijking klopt niet helemaal. De lucht in een kamer bestaat uit moleculen (stikstof, zuurstof, en nog wat andere stoffen) die we zouden kunnen detecteren zonder geluidsgolven te maken. Met een quantumveld kan dit niet. Het veld zelf is op echt geen enkele manier waarneembaar. Alleen de golven in het veld zien we, in de vorm van quantumdeeltjes.
Zodra we aannemen dat quantumdeeltjes bestaan uit golven, en niet uit puntdeeltjes, blijken veel van de dingen die in eerste instantie raar en paradoxaal lijken, eigenlijk heel gewoon.
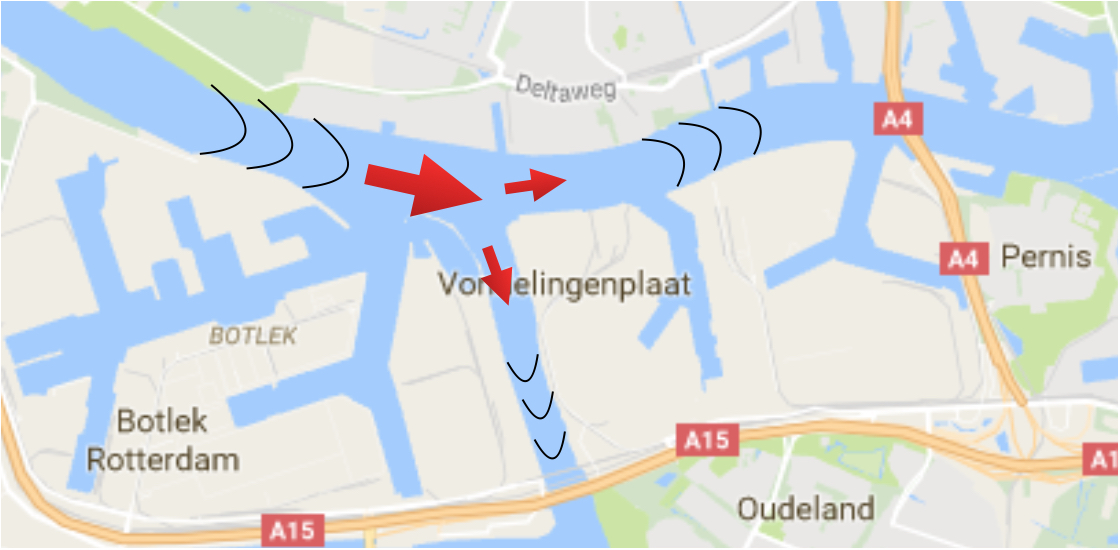
Afbeelding 2. Superpositie van watergolven.Één golf in de Nieuwe Waterweg stroomt tegelijkertijd zowel de Nieuwe als Oude Maas op.
Superposities
Quantumdeeltjes kunnen zich op twee plekken tegelijkertijd bevinden. Een enkel elektron kan op één en hetzelfde moment jouw kamer binnenkomen, en die van de buurvrouw. Dit klinkt raar, maar is een eigenschap die alle golven gemeen hebben. Als het op zee stormt en er flinke golven richting de kust komen, kan één golf via de Nieuwe Waterweg tegelijkertijd zowel de Oude als de Nieuwe Maas opgaan – zie afbeelding 2. Dat de golf zich splitst en zich zowel in de ene als in de andere rivier bevindt, verbaast niemand. Op dezelfde manier kun je als je nu hard op tafel slaat een geluidsgolf creëren die tegelijkertijd de kamers van je boven- en onderburen bereikt. De helft van de geluidsgolf die je gemaakt hebt bevindt zich dan in de ene kamer, en de helft in de andere. Als we zeggen dat een elektron zich in een superpositie bevindt, bedoelen we daarmee precies hetzelfde. De helft van de elektron-golf bevindt zich dan op één plek, en de helft op een andere.
Onzekerheidsrelaties
Als je van een quantumdeeltje weet hoe snel het beweegt, kun je onmogelijk weten waar het is. Sterker nog: een quantumdeeltje waarvan je de snelheid (of preciezer gezegd: de impuls) kent, heeft helemaal geen positie, en bevindt zich in een superpositie van alle mogelijke locaties. Het tegenovergestelde is trouwens ook waar. Als je weet waar een quantumdeeltje is, is zijn impuls volkomen onbepaald. Dit klinkt allemaal weer erg mysterieus, maar het is wederom een algemene eigenschap van alle golven.
Voor planeten, biljartballen en puntdeeltjes is de impuls gelijk aan de massa maal de snelheid. Als je van een bal met een bepaalde massa de snelheid kent, weet je dus ook zijn impuls. Voor watergolven in je badkuip thuis, of geluidsgolven in de kamer om je heen, is het niet zozeer de snelheid als wel de golflengte die bepaalt wat de impuls van de golf is. De snelheid van het geluid ligt immers vast, en is voor alle geluidsgolven hetzelfde. De golflengte hangt echter ook af van de frequentie, en is voor iedere golf anders. De relatie tussen golflengte, snelheid en frequentie wordt gegeven door de formule:
λ= v/f.
In deze vergelijking is λ de golflengte, v de snelheid, en f de frequentie. Voor quantumdeeltjes is het de golflengte die de impuls bepaalt, volgens de formule:
p= h/λ,
Hier is p de impuls, en de letter h geeft de constante van Planck weer. Die constante is een getal dat je kunt meten, en dat nooit verandert (net als bijvoorbeeld de lichtsnelheid of Newton’s zwaartekrachtsconstante).
Voor golven is de onzekerheidsrelatie tussen positie en impuls dus eigenlijk een verband tussen positie en golflengte, en die relatie kun je thuis in je badkuip gemakkelijk terugzien. De golflengte is de afstand waarover de vorm van een golf iedere keer exact herhaald wordt. Van de golf aan de linkerkant in afbeelding 3 hieronder kunnen we dus niet goed zeggen wat de golflengte is. Er is wel een patroon dat een beetje herhaalt wordt, maar na twee incarnaties houdt het op. Om een echt goed gedefinieerde golflengte te hebben moeten we een golf beschouwen zoals in het midden van afbeelding 3 hieronder. Deze golf herhaalt dezelfde vorm van het begin van het bad tot het eind, en we kunnen dus duidelijk zeggen wat de lengte van het zich herhalend patroon is. Van deze golf kunnen we echter onmogelijk zeggen waar hij zich bevindt. De golf strekt zich uit over de gehele badkuip, en de positie is dus volkomen onbepaald. Om de positie goed te kunnen bepalen, hebben we een golf nodig die lijkt op degene aan de rechterkant in het onderstaande afbeelding. Van deze golf kunnen we duidelijk zeggen waar hij is. Wat de golflengte van deze golf is, is echter volkomen onduidelijk. De golven die je maakt in bad kunnen dus onmogelijk tegelijkertijd een duidelijke positie én een duidelijke golflengte hebben. Op dezelfde manier kun je van quantumdeeltjes onmogelijk tegelijkertijd de impuls én de positie bepalen.

Afbeelding 3. Onzekerheidsrelatie voor gewone watergolven.Je bent pas zeker over een golflengte als de golf zich onafgebroken herhaalt. Is dit niet het geval, dan kun je nooit zeker zijn over wat de golflengte precies is, maar word je wel steeds zekerder van de positie van de golf.
Tunnelen
Een quantumdeeltje dat op een ondoordringbare muur afgeschoten wordt, kaatst niet altijd terug, maar kan ook aan de andere kant van de muur verschijnen en daar doorvliegen alsof er niets gebeurd is. Je zou zeggen dat dit soort tunnelen wel een vreemd quantumverschijnsel moet zijn. Maar nee, alweer kunnen alle soorten golven dit trucje uithalen. In dit geval is het niet zo heel eenvoudig om het effect te reproduceren in je badkuip, maar in principe kan het wel. Wat we nodig hebben is een effect dat je misschien wel kent uit de beschrijving van lichtstralen: totale interne reflectie. Als een lichtstraal vanuit bijvoorbeeld de bodem van een zwembad schuin naar boven gaat, zal hij bij het raken van het wateroppervlak een beetje van richting veranderen, en nog wat schuiner door de lucht verder reizen. Dit wordt breking van het licht genoemd. Als de straal echter té schuin gaat, en het wateroppervlak met een te grote hoek raakt, kan de straal zo ver gebroken worden dat hij het water helemaal niet meer verlaat, en in plaats daarvan terug naar beneden weerkaatst wordt. Een voorbeeld van zulke totale interne reflectie zie je in afbeelding 4 hieronder gedemonstreerd met een laserstraal in een stuk plexiglas.

Afbeelding 4. Totale interne reflectie.Bron: oberlin.edu
Als we in wat meer detail naar deze situatie kijken, moeten we ons echter realiseren dat licht eigenlijk bestaat uit electromagnetische golven, en niet uit stralen. Bij totale interne reflectie vormt het oppervlak van het plexiglas een muur waar die golven niet zomaar doorheen kunnen, en dus kaatsen ze terug. Dit gaat echter niet helemaal plotseling. Een golf is geen puntdeeltje. Hij heeft een golflengte, en is enigszins uitgespreid in de ruimte. Terwijl het licht weerkaatst wordt kan de golf niet exact gelokaliseerd zijn aan het oppervlak (door de onzekerheidsrelatie), en bevindt hij zich dus voor een deel nog in het plexiglas, maar ook voor een deel in de lucht. Laten we nu een tweede stuk plexiglas heel dicht bij het eerste brengen, zonder het er echt tegenaan te houden. Als we dichtbij genoeg zijn, kan tijdens de reflectie het uitstekende stuk golf vanaf het oppervlak van het eerste stuk plexiglas, via de tussenliggende lucht, in het tweede stuk plexiglas terecht komen. Eenmaal daar is er geen reden meer voor het licht om nog te reflecteren, en dus beweegt de golf zich verder alsof er niets gebeurd is. Dit verschijnsel wordt gefrustreerde totale interne reflectie genoemd, en je kunt zien dat het echt werkt in de onderstaande afbeelding.

Afbeelding 5. Gefrustreerde totale interne reflectie.Bron: oberlin.edu
Ook al is gefrustreerde totale interne reflectie het gemakkelijkst te demonstreren met laserlicht, het is een algemeen golfverschijnsel. Hetzelfde effect kun je ook krijgen met golven in water. Als je bijvoorbeeld een badkuip samenstelt uit twee stukken, waarvan het ene stuk veel dieper is dan het andere, dan zullen golven die je op de grens tussen de stukken afstuurt gebroken worden. Als die breking te groot wordt, treedt er totale interne reflectie op. Als we nu een badkuip nemen met drie stukken, waarvan het derde dezelfde diepte heeft als de eerste, en de het tweede, ondiepe stuk heel smal gemaakt wordt, kan een deel van de gereflecteerde golf door het verboden ondiepe stuk heen tunnelen, en onverstoord in het derde stuk bad verschijnen. Dit wordt gedemonstreerd in de foto’s hieronder, afbeelding 6. Voor quantumdeeltjes geldt nu precies hetzelfde. Bij het tegenkomen van een muur of barrière kan een deel van de golf erdoorheen lekken, en als de muur dun genoeg is zelfs aan de andere kant tevoorschijn komen.

Afbeelding 6. Gefrustreerde totale interne reflectie met watergolven.Bron: Education Development Center, Newton, MA USA
Echt rare dingen
Als al die ogenschijnlijk rare quantumdingen eigenlijk heel normale eigenschappen van golven zijn, en dus ook zonder quantummechanica kunnen bestaan, wat is er dan nog speciaal aan de wereld van de quantumtheorie? Wat is er nog quantum in de quantummechanica? De belangrijkste eigenschap waarin een quantumgolf essentieel verschilt van een geluidsgolf of watergolf, is het feit dat hij in zekere zin ondeelbaar is. Ook al is een quantumdeeltje een golf, en ook al kun je die golf echt uitspreiden op zo’n manier dat hij voor de helft in de ene kamer is en voor de helft in een andere, wanneer je het quantumdeeltje probeert vast te zetten of te detecteren, zal ogenblikkelijk de golf zodanig vervormen dat je ofwel het volledige deeltje vindt, of niets. Hoe uitgespreid de quantumgolf ook is, alle stukken van de golf zijn altijd zodanig met elkaar verbonden dat je in een meting nooit een half quantumdeeltje aantreft.
Dit is natuurlijk niet zo voor golven buiten de quantummechanica. Een geluidsgolf die zich van de ene naar de andere kamer verspreidt wordt wel degelijk in allebei de kamers gehoord. En wat je hoort is daarbij maar een gedeelte van de geluidssterkte die de golf bij het verlaten van de speaker had. Op dezelfde manier kun je een watergolf die zich splitst in twee rivierarmen prima uitdoven in de ene arm, zonder de achtergebleven golf in de andere arm te beïnvloeden.
Hoe verschillende onderdelen van een quantumgolf precies met elkaar verbonden blijven, en hoe ze allemaal weer bij elkaar komen zodra het quantumdeeltje geabsorbeerd of gedetecteerd wordt, is niet helemaal duidelijk. Dit is nog altijd onderwerp van onderzoek aan de frontlinie van moderne natuurkunde. Het is echter wel duidelijk geworden uit de vele experimenten die er de afgelopen decennia gedaan zijn, dat quantumdeeltjes deze vorm van ondeelbaarheid bezitten. De quantumtheorie, inclusief de aannames dat quantumdeeltjes golven zijn en dat ze desondanks niet voor de helft gedetecteerd kunnen worden, is tot op uitzonderlijke nauwkeurigheid getest. Quantummechanica is zelfs verreweg de best geteste theorie in de gehele natuurkunde, en er is dus geen twijfel mogelijk dat het zien van quantumdeeltjes als ondeelbare golven een goede en nauwkeurige beschrijving van de natuur oplevert.
Teleportatie
Dat bij een detectie een uitgespreide quantumgolf vliegensvlug gelokaliseerd wordt op slechts één lokatie, klinkt misschien alsof je het zou kunnen gebruiken om een machine te maken waarmee elektronen of andere quantumdeeltjes sneller dan het licht van de ene plaats naar de andere gestuurd kunnen worden. Dit blijkt echter niet mogelijk, en dat is maar goed ook, want dat zou in strijd zijn met een andere uitzonderlijk goed geteste theorie in de natuurkunde, namelijk Einsteins speciale relativiteitstheorie.
Wat echter wel kan, is een teleportatiemachine bouwen voor quantumdeeltjes. Hierbij prepareer je eerst een speciale golf van meerdere quantumdeeltjes. De quantumgolven van de afzonderlijke deeltjes zijn hierbij op zodanige wijze met elkaar verstrengeld, dat je een van de deeltjes op de ene plek kunt vernietigen (detecteren), en dan zeker weet dat tegelijkertijd een deeltje met precies dezelfde eigenschappen op een andere plek ontstaat (gedetecteerd kan worden). Het is dus alsof een quantumdeeltje van de ene plek naar de andere gestraald kan worden. Natuurlijk zijn er nog steeds restricties: het hele proces staat geen transport van deeltjes sneller dan de snelheid van het licht toe, en om de teleportatiemachine te bouwen moet er eerst een verstrengelde golf gecreëerd worden, die zich op de traditionele manier van de ene plek naar de andere moet uitspreiden.
Dat teleportatie desondanks geen science fiction is, en echt gedaan kan worden met quantumdeeltjes, is inmiddels experimenteel aangetoond. Dit is iets dat echt nooit zou kunnen met water- of geluidsgolven, en maakt op een mooie manier de ware aard en magie van de quantummechanica duidelijk.