Quantumfysica (2): Zwarte stralers

In het vorige artikel hebben we gezien dat licht voor lijkt te komen in kleine pakketjes: quanta. Hoe groot zijn die quanta precies? Iets preciezer: hoeveel energie bevat één lichtquantum? Dat zouden we natuurlijk kunnen uitrekenen aan de hand van het foto-elektrisch effect dat we in dat artikel bespraken. Historisch werd de grootte van quanta echter voor het eerst bepaald vanuit een heel ander fenomeen: de straling van zwarte stralers. We zullen in dit artikel zien hoe dat in zijn werk ging.

Wanneer is een voorwerp perfect zwart? Het antwoord ligt voor de hand: als het helemaal geen licht weerkaatst. In de natuurkunde spreken we in dat geval van een zwart lichaam. Let op: als we “helemaal geen licht” zeggen, bedoelen we niet alleen het zichtbare licht! Zichtbaar licht vormt, zoals we inmiddels weten, maar een heel klein deel van het totale spectrum van elektromagnetische straling. Een perfect zwart lichaam weerkaatst ook geen infrarood licht, geen UV-straling, geen radiostraling, enzovoort. In de praktijk zullen voorwerpen natuurlijk nooit perfect zwart zijn, maar we kunnen voorwerpen zwart genoeg maken om er relevante experimenten mee te doen.

Een zwart lichaam is dus een voorwerp dat geen licht weerkaatst. Wil dat zeggen dat een zwart lichaam ook geen licht uitzendt? Dat laatste blijkt niet het geval te zijn. We weten uit de praktijk dat voorwerpen uit zichzelf licht gaan uitzenden als ze warm worden. Het uitzenden van licht is namelijk een heel efficiënte manier om overtollige energie kwijt te raken. Denk aan een ijzeren staaf die een smid in het vuur houdt: op een gegeven moment zal die staaf “roodgloeiend” worden. Dat wil zeggen: de staaf begint uit zichzelf energie af te staan door rood licht uit te zenden.

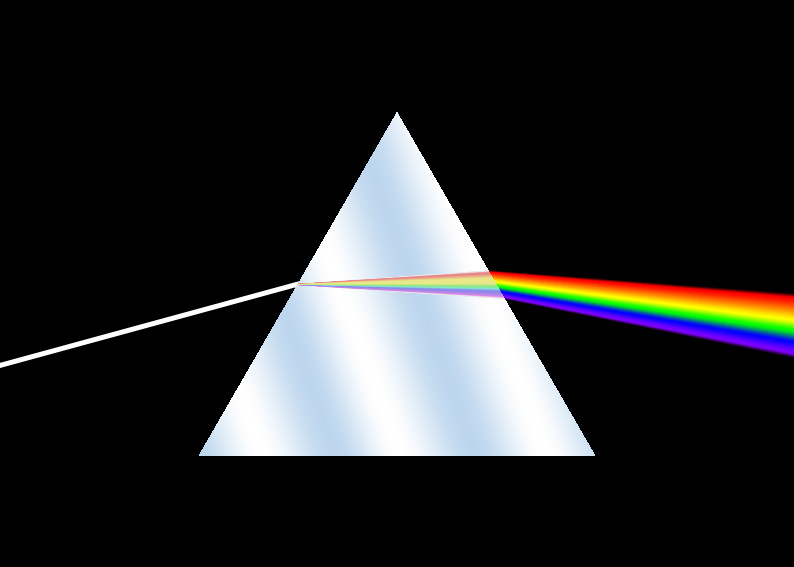
Afbeelding 1. Licht in een prisma.Wat wij als wit licht zien, is een combinatie van alle kleuren uit het spectrum. Dat is goed te zien wanneer we het witte licht met een prisma weer ontrafelen in een “regenboog” van alle kleuren. Als een voorwerp zo warm is dat het alle kleuren licht uitstraalt, zien we dat voorwerp als “witheet”. Afbeelding: Wikipedia-gebruiker Florenco.

De kleur licht die een voorwerp uitzendt hangt af van zijn temperatuur. Ook dat kunnen we zien aan de ijzeren staaf: als de smid die lang genoeg in een heet vuur houdt, zal de staaf “witheet” worden. Eerst zond de staaf voornamelijk rood licht uit, maar als de temperatuur hoger wordt, worden ook kleuren licht met kortere golflengtes in grote hoeveelheden uitgezonden, en zien we dus alle kleuren licht tegelijk. Die combinatie van alle kleuren ziet ons oog als wit licht (zie afbeelding 1). Als we de staaf nog warmer zouden maken, bijvoorbeeld met een goede lasbrander, zou de staaf vooral blauw licht gaan uitzenden.

Dat warmere voorwerpen licht van kortere golflengtes uitzenden, is na het vorige artikel goed te begrijpen. We hebben immers gezien dat licht met een kortere golflengte een hogere frequentie heeft, en dat licht met een hogere frequentie meer energie bevat. Als een voorwerp meer energie kwijt wil raken, kan dat dus het efficiëntst door licht met kortere golflengtes uit te zenden.

Natuurkundigen maken hun beschrijvingen graag zo exact mogelijk, dus dit alles roept de vraag op: als we een voorwerp tot een bepaalde temperatuur opwarmen, kunnen we dan precies bepalen hoeveel licht van welke golflengte er wordt uitgezonden? Om die vraag te beantwoorden zijn zwarte lichamen erg nuttig. Een zwart lichaam reflecteert namelijk zelf geen licht, en dus weten we dat al het licht dat we van een zwart lichaam opvangen door het lichaam zelf is uitgezonden. Zodra een zwart lichaam licht uitzendt, noemen we het ook wel een zwarte straler. Aan een zwarte straler kun je dus precies meten hoeveel licht er van welke golflengte wordt uitgezonden. Een grafiek waarin de lichtintensiteit voor elke golflengte wordt weergegeven noemen we een spectrum van de zwarte straler.

Dergelijke spectra werden al in de 19e eeuw met grote precisie gemeten. Ze leidden uiteindelijk tot de grafiek die te zien is in afbeelding 2. In de afbeelding staat het spectrum getekend voor verschillende temperaturen van het zwarte lichaam. We meten de temperatuur hier in Kelvin – een temperatuurschaal die ten opzichte van de Celsius-schaal 273 graden is opgeschoven, zodat het absolute temperatuurnulpunt van grofweg -273°C gelijk is aan 0K. Een temperatuur van 6000K is daarmee bijvoorbeeld gelijk aan 6000-273=5737°C, enzovoort.

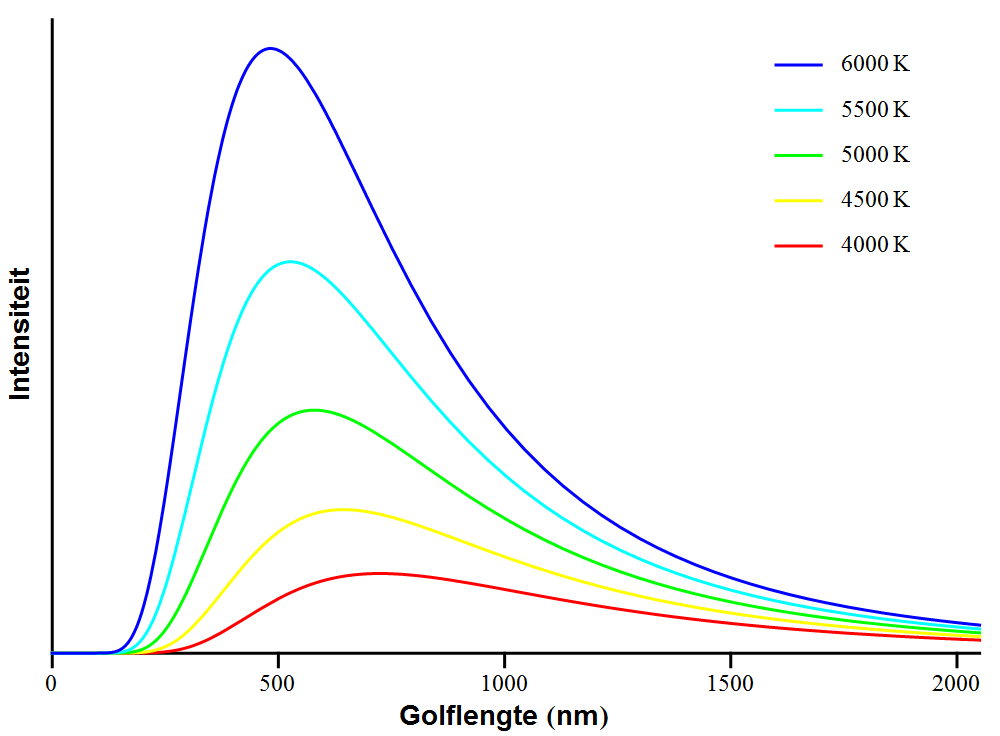
Afbeelding 2. Het specturm van een zwarte straler.Het spectrum is hier weergegeven voor verschillende temperaturen, van 4000K tot 6000K.

We zien in afbeelding 2 dat een zwarte straler met een temperatuur van 4000K (de onderste, rode lijn) veel minder licht uitzendt dan een zwarte straler met een temperatuur van 6000K (de bovenste, blauwe lijn). Verder zien we dat de piek van de rode lijn verder naar rechts ligt dan die van de blauwe lijn. De zwarte straler met een temperatuur van 4000K zendt het meeste licht uit bij een golflengte van ongeveer 700nm; de zwarte straler met een temperatuur van 6000K zendt het meeste licht uit bij een golflengte van iets meer dan 500nm. De straler van 4000K zien we dus als “roodgloeiend”, al wordt er bij deze temperatuur al zoveel ander licht uitgezonden dat de kleur die we waarnemen eerder wit-oranje zal zijn. De straler van 6000K zal er veel blauwwitter uitzien.

Natuurkunde is echter niet alleen beschrijven, maar ook begrijpen. Kunnen we ook begrijpen waarom de spectra in afbeelding 2 grofweg de vorm hebben die ze hebben? Met name: waarom is er überhaupt ergens een maximum in de intensiteit – waarom wordt licht met zowel heel korte als heel lange golflengtes veel minder uitgezonden?

Het bleek niet eenvoudig om deze vraag te beantwoorden. Diverse pogingen leidden tot antwoorden die het spectrum uit afbeelding 2 ofwel heel goed beschreven bij lange golflengtes, ofwel heel goed bij korte golflengtes, maar zelden allebei. De Engelse natuurkundigen Lord Rayleigh en James Jeans stelden bijvoorbeeld in 1900 een model op dat het spectrum bij lange golflengten heel goed beschreef. Ze vergeleken de zwarte straler grofweg met een gitaarsnaar. Zo’n snaar kan met verschillende golflengtes trillen (zie afbeelding 3): de golflengte kan gelijk zijn aan de lengte van de snaar, maar ook twee-, drie-, vier- (of honderd-) maal zo klein. Overigens: om technische redenen wordt een golflengte meestal gedefinieerd als tweemaal de lengte tussen twee “knooppunten”, dus eigenlijk moeten we zeggen dat de helft van de golflengte gelijk kan zijn aan de lengte van de snaar of een fractie daarvan.  Dat technische detail maakt voor het uiteindelijke rekenwerk wel uit, maar in onze algemene beschrijving hieronder niet.

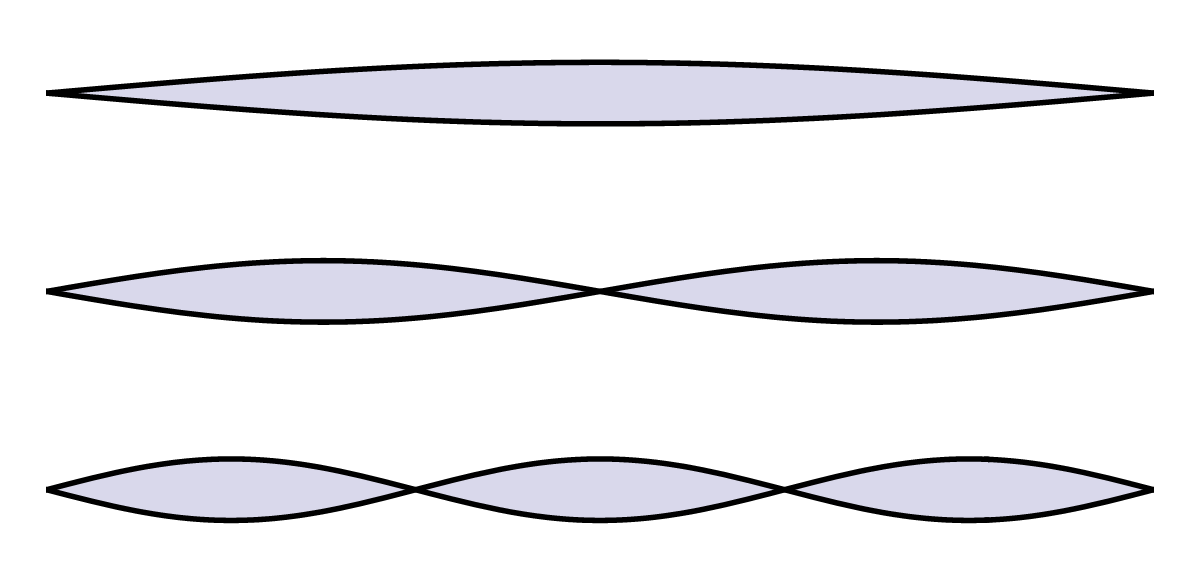
Afbeelding 3. Trillingen in een snaar.De snaar kan in de “grondtoon” trillen (bovenste afbeelding), maar er kunnen ook meerdere (halve) golflengtes op de snaar passen: boventonen.

Als we een gitaarsnaar met een lengte van een meter hebben, kunnen daar dus golven in voorkomen met een (halve) golflengte van 100 cm, 100/2 = 50 cm, 100/3 = 33cm, 100/4 = 25 cm, enzovoort. We zien dat die golflengtes steeds dichter bij elkaar komen te liggen: het verschil in (halve) golflengte tussen de eerste twee is 50 cm, maar tussen de laatste twee maar 8 cm. Kortom: bij kortere golflengtes zitten “in een klein stukje spectrum” veel meer mogelijke golflengtes dan bij langere golflengtes. Als we nu aannemen dat elke mogelijke manier van trillen ongeveer evenveel energie bevat (een aanname die bekend staat als “equipartitie”, en die in veel fysische systemen de energieverdeling heel goed blijkt te beschrijven) zien we dat er bij korte golflengtes in een klein stukje spectrum dus ook veel meer energie opgeslagen moet zijn. Met andere woorden: hoe korter de golflengte, hoe hoger de intensiteit.

Dit model heeft een goede kans om de rechter helft van het spectrum in afbeelding 2 te beschrijven: hoe korter de golflengte wordt, hoe hoger de intensiteit van het uitgezonden licht. Met het nodige rekenwerk bleek het met het model van Rayleigh en Jeans inderdaad mogelijk om de vorm van de lijnen in afbeelding 2 heel goed te beschrijven bij lange golflengtes. Aan de andere kant is duidelijk dat het model bij korte golflengtes nooit kan kloppen: volgens het model zou de intensiteit immers alleen maar groter moeten worden bij kortere golflengtes, terwijl we in afbeelding 1 zien dat de intensiteit op een gegeven moment weer kleiner wordt.

Er waren ook modellen die juist het deel van het spectrum bij kortere golflengtes goed beschreven. Zo had de Duitse natuurkundige Wilhelm Wien al in 1896 een thermodynamisch model opgesteld dat dat deed. De details van dat model zijn te ingewikkeld om hier kort uit te leggen, maar het resultaat was precies het omgekeerde van dat van Rayleigh en Jeans: Wien’s model beschreef heel goed de toename van de intensiteit als je van heel korte naar iets langere golflengtes ging, maar kon juist niet verklaren dat de intensiteit bij nog langere golflengtes weer afnam.

Uiteindelijk gaf de Duitse fysicus Max Planck in oktober van het jaar 1900, heel kort na het verschijnen van het model van Rayleigh en Jeans, de oplossing van het raadsel. Planck ontdekte dat het probleem met alle bestaande modellen was dat erin werd aangenomen dat de energie in het licht in willekeurige hoeveelheden kon voorkomen. Hij stelde een model op waarin licht alleen in kleine pakketjes – de inmiddels bekende quanta – kon voorkomen. Planck gaf ook aan hoe groot die pakketjes precies waren: voor licht met een bepaalde golflengte λ, en een bijbehorende frequentie ν, was de hoeveelheid energie (E) in één pakketje gelijk aan

E = h ν.

In woorden: de energie van één pakketje kon eenvoudig berekend worden door de frequentie met een bepaald getal h te vermenigvuldigen. Die verhoudingsfactor, h, was een nieuwe, door Planck voorspelde natuurconstante, waarvan de grootte nog bepaald moest worden.

Afbeelding 4. Max Planck.

Planck baseerde zijn model op het eerdere model van Wien, en bij korte golflengtes was het resultaat dan ook precies de linkerhelft van het spectrum dat Wien’s model ook erg goed voorspelde. Vanuit het idee van energiepakketjes is dat ook goed te begrijpen: bij korte golflentes is de frequentie heel hoog, en is dus heel veel energie nodig om één quantum te produceren. Bij te korte golflengtes wordt het daardoor eenvoudigweg te moeilijk voor de zwarte straler om nog voldoende grote energiequanta te produceren.

Het mooie van Plancks model was echter dat voor licht van lange golflengtes de frequentie heel klein is, zodat de energiepakketjes voor lange golflengtes ook enorm klein zijn. Het feit dat energie alleen in pakketjes voorkomt is bij lange golflengtes dus nauwelijks nog waarneembaar – net zoals bij een computerscherm met heel kleine pixels de grootte van de pixels nauwelijks waarneembaar is, en we dus nauwelijks zien dat het beeld eigenlijk niet echt vloeiend is. Kortom: bij lange golflengtes leek het net alsof de totale energie van het licht wél in willekeurige, continue hoeveelheden kon voorkomen. Het resultaat was dat het “discrete” model van Planck juist voor lange golflengtes erg leek op het “continue” model van Rayleigh en Jeans. Het model beschreef dus beide uiteinden van het spectrum goed – en bleek ook het gebied rond de piek perfect te beschrijven.

Afbeelding 5. Het artikel van Planck.Het artikel waarin Max Planck in 1900 zijn idee van quanta uiteenzette.

De vraag wat de precieze waarde van de vermenigvuldigingsfactor h is, was nu ook eenvoudig te beantwoorden. Die waarde moest immers zo gekozen worden dat het voorspelde spectrum uit het model van Planck precies overeenkwam met de lijnen in afbeelding 2. Planck bepaalde de grootte van deze constante, die sindsdien bekend staat als de constante van Planck. Inmiddels, met veel betere metingen, is de constante tot op hoge precisie bepaald: de waarde is

h ≈ 6,62606957 10^-34 J/Hz.

Let op de eenheden: in de formule E = h ν meten we energie in joules (J) en frequentie in hertz (Hz), dus de eenheid van de constante is joule per hertz. Omdat een hertz een aantal trillingen per seconde is, is de eenheid hertz het omgekeerde van de eenheid seconde, en kunnen we de eenheid van h dus ook schrijven als J·s.

De constante van Planck is zoals we zien enorm klein: in niet-wetenschappelijke notatie zouden we die schrijven als 0,000000000000000000000000000000000662606957 J·s. Licht komt dus weliswaar voor in pakketjes, maar die pakketjes zijn zo minuscuul dat we die in het dagelijks leven absoluut niet waarnemen. In vrijwel alle experimenten op macroscopische schaal lijkt energie in willekeurige, continue hoeveelheden te kunnen voorkomen. Pas als we experimenten gaan doen op de schaal van atomen en nog kleiner wordt het van belang dat energie voorkomt in discrete quanta. De quantumtheorie is daarom een theorie die vooral nodig is om verschijnselen op een dergelijke microscopische schaal te beschrijven.

Overigens was Planck zelf nog verre van overtuigd van het feit dat de energiequanta ook werkelijk fundamenteel waren: hij noemde het idee van quanta een “postulaat”, en gebruikte het met name als een wiskundige truc om het spectrum van de zwarte stralers te beschrijven. Pas toen Einstein in 1905 het foto-elektrisch effect verklaarde aan de hand van dezelfde quanta werd volledig duidelijk dat de “lichtdeeltjes” echt bestonden, en heel duidelijk waarneembare fysische effecten hadden.

Daarmee weten we nu dus dat lichtquanta bestaan, en hoe groot ze precies zijn. Maar de vraag blijft: is licht dan dus een deeltjesproces, en geen golfproces? En als dat zo is, hoe komt het dan dat licht ook zo veel golfverschijnselen vertoont? In de volgende twee artikelen beantwoorden we deze centrale vraag uit de quantummechanica.

Dit is het tweede artikel uit het dossier Quantumfysica. In het derde artikel stellen we de belangrijke vraag of licht nu uit golven of uit deeltjes bestaat.