
Afbeelding 1. Bliksem.Wanneer geleidt iets wel elektriciteit, en wanneer niet? Het blijkt dat quantummechanica cruciaal is om het antwoord op deze schijnbaar eenvoudige vraag te kunnen begrijpen. Foto: Edward Aspera Jr., US Air Force.
- Geleiden of niet geleiden?
- Golven of deeltjes?
- Golflengte, snelheid en impuls
- Meer dimensies
- Golven optellen
- The road ahead
Geleiden of niet geleiden?
In het dagelijks leven komen we allerlei materialen tegen die goed elektrische stroom kunnen geleiden. Het gaat daarbij met name om metalen: koper, ijzer, aluminium, enzovoort. Verbind een batterij met twee koperdraadjes aan een lampje, en het lampje zal gaan branden. Er loopt via de koperdraadjes elektrische stroom het lampje in en uit, en in het lampje verhit die stroom een gloeidraad die daardoor licht en warmte gaat uitzenden. Materialen die elektrische stroom geleiden noemen we, niet geheel verrassend, geleiders.
Niet elk materiaal geleidt echter stroom. Vervang de koperdraadjes door een wollen draad, een strip plastic of een rubberen elastiekje, en het lampje zal uit blijven. Sommige materialen geleiden dus niet of nauwelijks stroom; dergelijke materialen noemen we isolatoren. En dan zijn er nog bijzondere materialen zoals silicium die we halfgeleiders noemen: materialen die in het algemeen minder stroom doorlaten dan geleiders, maar dat wel op een bijzondere manier doen. Zo gaan metalen de stroom meestal slechter geleiden als we ze opwarmen, maar gaan halfgeleiders dat juist beter doen. Verder kunnen we halfgeleiders de stroom veel beter laten geleiden door ze te mengen met een minieme fractie van een ander materiaal – de zogeheten doping.
Wat bepaalt al deze enorm verschillende elektrische eigenschappen van materialen? Waarom geleidt koper wel stroom, en water niet? Alle materialen om ons heen zijn opgebouwd uit atomen, die we ons grofweg kunnen voorstellen als positief geladen kernen waar negatief geladen elektronen omheen cirkelen – zie afbeelding 2. Het zijn de negatief geladen elektronen die de elektrische stroom vormen: als zij vrij door een materiaal heen kunnen bewegen, is het materiaal een geleider. Kunnen ze dat niet, dan is het materiaal een isolator.
Maar wat zorgt ervoor dat een elektron vrij is om zijn ‘eigen’ atoomkern te verlaten en door een materiaal heen te bewegen? Het antwoord blijkt verrassend ingewikkeld, en kan alleen begrepen worden aan de hand van de quantummechanica. Met andere woorden: om de alledaagse elektrische stroom te begrijpen, moeten we ophouden met atomen te zien als kleine planetensteltjes, en ze daadwerkelijk als quantummechanische objecten gaan beschouwen. Dat zal dan ook in dit en de volgende artikelen ons doel zijn.
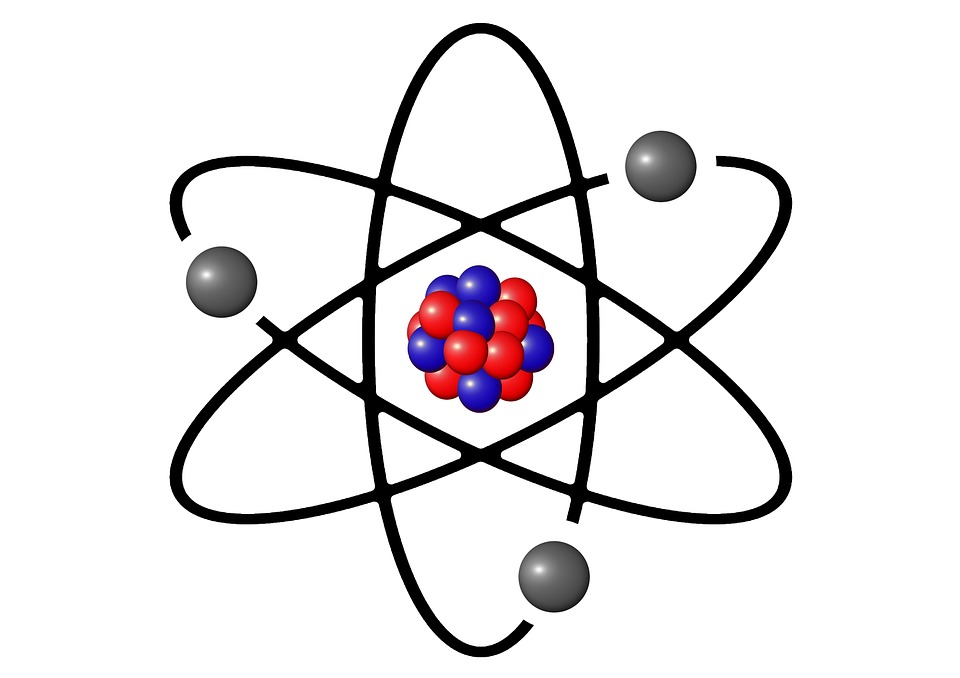
Afbeelding 2. Een ‘klassiek’ atoom,In het klassieke beeld van een atoom stellen we het ons voor als een mini-planetenstelsel, met de positief geladen kern in het midden en elektronen als negatief geladen puntdeeltjes die daaromheen draaien. Om geleiding te begrijpen moeten we dit beeld laten varen, en de elektronen zien als quantummechanische golven. Afbeelding: Wikipedia-gebruiker Halfdan.
Golven of deeltjes?
Misschien wel het belangrijkste grondbeginsel van de quantummechanica is het feit dat we elektronen en andere elementaire deeltjes niet moeten zien als kleine puntvormige kogeltjes, maar als golven. Net als een golf op het water, is een elektron nooit precies op één plaats. Een elektrongolf heeft pieken, waar het elektron ‘heel veel is’, en dalen, waar het elektron ‘niet of nauwelijks is’. Pas als we een meting doen aan het elektron vinden we het op één plaats, maar zolang we het elektron met rust laten, zal de elektrongolf zich verspreiden, en is het elektron dus als het ware op heel veel plaatsen tegelijk.
Lastig om je voor te stellen? Dat zeker – we zijn in ons dagelijks leven immers gewend dat voorwerpen altijd een vaste plaats hebben, en dat ook andere eigenschappen (snelheid, energie, enzovoort) van voorwerpen vaste waardes aannemen. In de quantumwereld is dat echter niet het geval. Wie meer hierover wil weten kan zijn hart ophalen in het dossier over quantumfysica dat eerder op deze site verscheen.
Het blijt dat juist de golfeigenschappen van het elektron cruciaal zijn om elektrische geleiding te begrijpen. De elektrongolven zeggen namelijk niet alleen iets over de plaatsen waar het elektron zich wel en niet kan bevinden; ze zeggen ook iets over de snelheden die het elektron kan hebben, en die snelheden bepalen natuurlijk de beweging van het elektron, en dus de elektrische stroom.

Afbeelding 3. Golven of deeltjes?Op quantumniveau is het het beste om elektronen te beschrijven als golven. Net als watergolven hebben ze geen vaste plaats, maar zijn elektronen ‘een beetje hier, en een beetje daar’. Foto: Paul Doherty.
Golflengte, snelheid en impuls
Elke regelmatige (in nettere termen: vlakke) golf, heeft een golflengte en een snelheid. Zie bijvoorbeeld afbeelding 4 hieronder, waar we een golf hebben getekend die zich in één richting voortbeweegt.
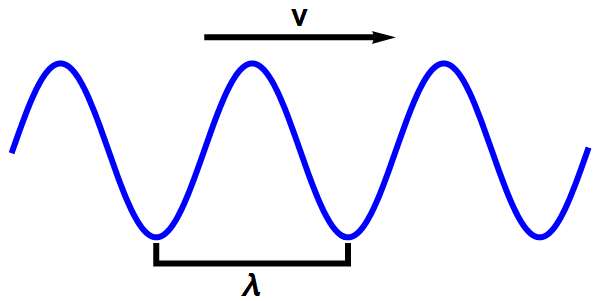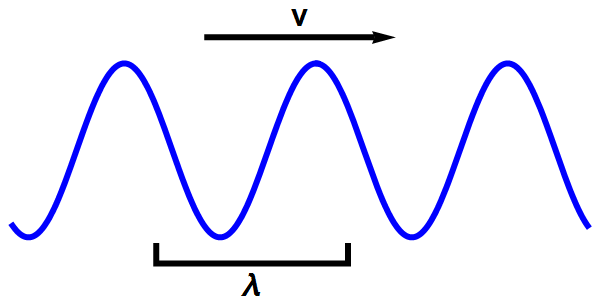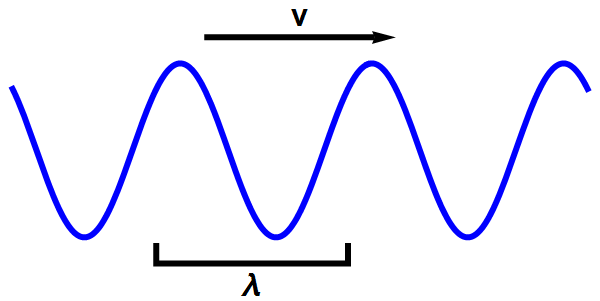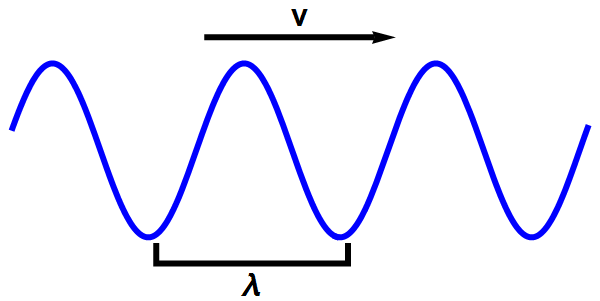
Afbeelding 4. Een vlakke golf in één dimensie.Een vlakke (sinusvormige) golf heeft een golflengte, λ, en een snelheid, v.
Een verrassend resultaat van de quantummechanica is nu dat de golflengte en de snelheid van een quantumgolf niet onafhankelijk van elkaar zijn. Golven met een twee keer zo kleine golflengte, blijken ook twee keer zo snel te bewegen; golven met een drie keer zo lange golflengte bewegen drie keer zo langzaam. In een nette formule: we kunnen de snelheid v van een elektrongolf uitrekenen als
v = h / (m λ).
In deze formule is λ de golflengte van de elektrongolf, m de massa van het elektron, en h een natuurconstante die de constante van Planck heet. Meestal wordt deze formule overigens iets anders geschreven: we kunnen links en rechts met de elektronmassa m vermenigvuldigen, en vinden dan
m v = h / λ.
De combinatie m v, het product van de snelheid van het elektron en zijn massa, wordt ook wel de impuls genoemd, en vaak aangegeven met de letter p. We kunnen bovenstaande relatie dus ook schrijven als
p = h / λ.
Deze relatie tussen impuls p en golflengte λ – de één is omgekeerd evenredig aan de ander – wordt ook wel de De Broglie-relatie genoemd.
Meer dimensies
Nu beweegt een elektrongolf natuurlijk niet in één, maar in drie dimensies. Tekenen in drie dimensies is wat lastig, dus laten we om te beginnen eens kijken hoe het bovenstaande verhaal er in twéé dimensies uit zou zien. Een vlakke golf heeft dan in elk van de twee richtingen een golflengte – zie afbeelding 5.
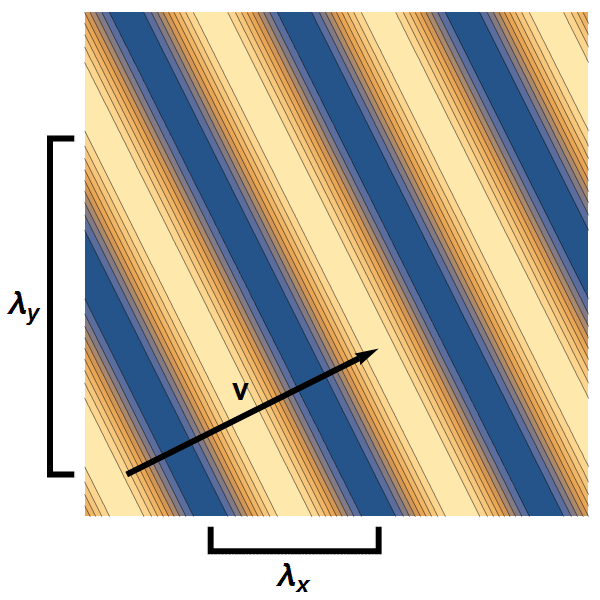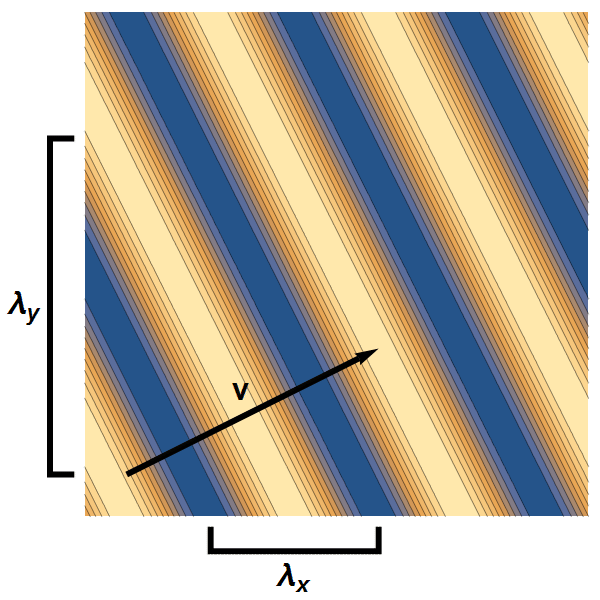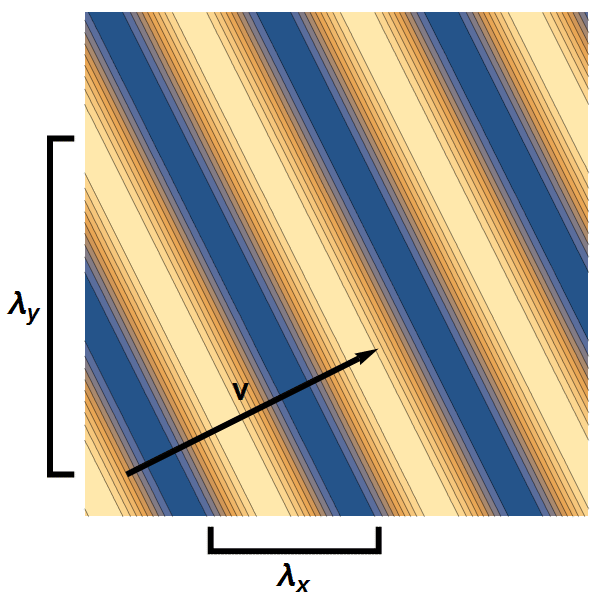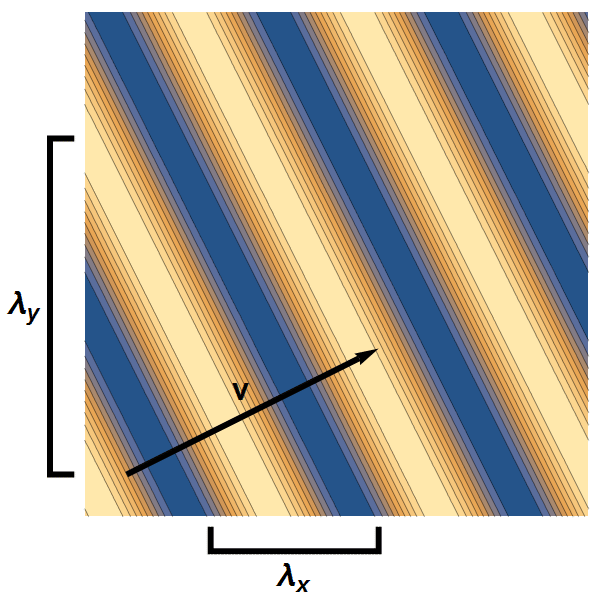
Afbeelding 5. Een vlakke golf in twee dimensies.We kunnen in elke richting de golflengte van de golf meten: λx en λy. De snelheidscomponent in beide richtingen is omgekeerd evenredig met de golflengte in die richting (in dit voorbeeld: de golf beweegt twee keer zo snel in de x-richting als in de y-richting), wat als gevolg heeft dat de golf zich loodrecht op de golffronten voortbeweegt.
Hoe zit het dan met de snelheid – of beter: de impuls – van de elektrongolf? Uit de de Broglie-relatie lijken we ook twéé snelheden te vinden. Dat is echter niet zo vreemd: in twee dimensies heeft een snelheid namelijk ook een richting – oftewel, een beweging in twee dimensies is opgebouwd uit twee componenten: een component in de horizontale richting en een component in de verticale richting. In nette wiskundige termen: een tweedimensionale snelheid is een vector – een pijltje waarvan het eindpunt twee coördinaten heeft. Voor elk van de componenten van die vector geldt de De Broglie-relatie, en zo vinden we uit de twee golflengtes van de golf precies de tweedimensionale snelheid.
In drie dimensies geldt hetzelfde: een vlakke golf heeft daar drie golflengtes, en die drie golflengtes bepalen precies de drie componenten van de driedimensionale snelheidsvector.
Golven optellen
De oplettende lezer zal misschien opmerken dat lang niet elke golf in de natuur eruit ziet als de golven in de afbeeldingen 4 en 5. Golven kunnen ook één gelocaliseerde piek hebben (denk aan een golf in de zee die naar het strand toe rolt), of kunnen bijvoorbeeld cirkelvormige golffronten in plaats van rechthoekige hebben – zie de watergolven in afbeelding 3.
Twee belangrijke eigenschappen van quantumgolven maken het echter zeer nuttig om ons de elektrongolven toch voor te stellen als vlakke golven. De eerste eigenschap is een eigenschap van golven in het algemeen: elke golfvorm blijkt gemaakt te kunnen worden als een combinatie van vlakke golven – zie bijvoorbeeld afbeelding 6. Deze procedure staat bekend onder de naam Fourier-decompositie. Wanneer we alles weten over het gedrag van vlakke golven, kunnen we dus alle eigenschappen van willekeurig gevormde golven daaruit afleiden!
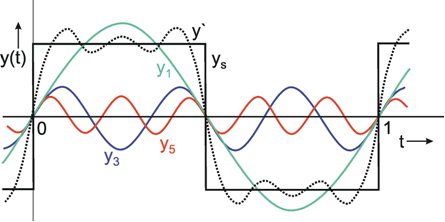
Afbeelding 6. Fourier-decompositie.In plaats van een vlakke, sinusvormige golf bekijken we hier een rechthoekige golf ys, weergegeven als de zwarte doorgetrokken lijn. Een redelijke benadering van deze golfvorm is de groene vlakke golf y1. Een nog betere benadering krijgen we door bovenop dit golfpatroon nog eens de golven y3 en y5 te maken: de gecombineerde golf y’ is de gestippelde lijn. Door dit proces voort te zetten kan een willekeurige golfvorm gemaakt worden uit vlakke, sinusvormige golven. Afbeelding: Holk Cruse, Bielefeld University.
De tweede belangrijke eigenschap van vlakke golven is specifiek voor quantumgolven: het blijkt dat vlakke golven namelijk in de systemen die voor ons van belang zijn een goed gespecificeerde energie hebben. Dat klinkt misschien verrassend – zijn er dan ook systemen die géén goed gespecificeerde energie hebben? Jazeker: net zoals in de quantummechanica elektronen geen vastliggende plaats hebben, hoeft ook hun energie niet één specifieke waarde aan te nemen. Kijk bijvoorbeeld weer eens naar de rechthoekige golf in afbeelding 6. Deze golf is opgebouwd uit een aantal vlakke golven, maar die vlakke golven hebben allemaal verschillende golflengtes, en – zoals we uit de De Broglie-relatie weten – dus ook allemaal verschillende snelheden. De energie van een elektrongolf hangt van zijn snelheid af (volgens de bekende formule Ekin = 1/2 m v2) en dus heeft een niet-vlakke golf zoals in afbeelding 6 ook een heel spectrum van verschillende energieën.
Nu is het in de natuurkunde vaak zo dat systemen de toestand van laagst mogelijke energie opzoeken. In het volgende artikel zullen we zien dat dit betekent dat juist de vlakke golven, met heel specifieke energie, een cruciale rol spelen in het begrijpen van de elektrische geleiding van materialen.
The road ahead
Goed, elektronen zijn dus golven, met een bepaalde golflengte en een daaruit volgende snelheid, impuls en energie. Hoe kunnen we vanuit dat beeld nu de geleiding van elektriciteit begrijpen? Dat zullen we in de komende artikelen in twee stappen doen.
Allereerst zullen we in het volgende artikel gaan kijken naar elektronen als golven in het materiaal zelf – golven die zich dus over relatief grote afstanden in het metaal kunnen uitspreiden. We zullen zien dat een belangrijk quantummechanisch principe, het uitsluitingsprincipe van Pauli, ervoor zorgt dat de elektronen met enorme snelheden door een geleidend materiaal bewegen, en dat die snelheden maar een heel klein beetje aangepast hoeven te worden om een stroom door het materiaal te laten lopen.
Daarmee kunnen we geleiding beschrijven, maar kunnen we nog niet verklaren waarom sommige materialen wel geleiden en andere niet. Het zal blijken dat we die eigenschappen echter ook kunnen begrijpen als we de elektronen bovendien zien als golven die beïnvloed worden door de positief geladen kernen in het materiaal. Dat zal ons leiden tot het concept van energiebanden, en daarmee kunnen we uiteindelijk geleiders, isolatoren en halfgeleiders begrijpen.
Dit is het eerste artikel uit het dossier ‘Quantumtoepassingen’. Het tweede artikel zal verschijnen op vrijdag 11 maart,