Ultrakoude gassen (3): verdampen en meten

Afbeelding 1. Een opstelling om atomen mee af te koelen.Foto: Florian Schreck.

In deze serie over ultrakoude gassen beschrijf ik in detail hoe men nou eigenlijk een ultrakoud gas in de praktijk maakt. In deel 1 en deel 2 van de serie hebben we al een groot aantal van de stappen gezien die daarvoor nodig zijn. Het voorbeeld van het productieproces van een Bose-Einstein condensaat bracht ons van een heet gas (rond 500 kelvin) van strontiumatomen, via laserkoeling, molassekoeling en Sisyphuskoeling, tot een eindtemperatuur van 1 tot 30 microkelvin. Maar zoals ik in beide artikelen benadrukt heb: dit is niet genoeg! Om een gas ultrakoud te noemen, moeten we het echt afkoelen tot enkele (honderden) nanokelvin. Om zo’n temperatuur te bereiken introduceren we de laatste fase van afkoelen: evaporative cooling, oftewel: koeling door verdampen. Dat proces gaat beslist niet vanzelf. Aan het eind van het vorige deel van deze serie artikelen is duidelijk gemaakt dat onze methode om het gas vast te houden niet meer volstaat: we bereiken een theoretische limiet, de Dopplerlimiet. We moeten voorbij die limiet dus een nieuwe manier vinden om ons gas beet te houden. Als dit al lukt, én we kunnen het gas verder afkoelen, dan moeten we nog één probleem oplossen: hoe wéét je nu eigenlijk wat de temperatuur van je gas is, en in welke toestand het zich bevindt? Met andere woorden: we moeten een meting uitvoeren om erachter te komen wat voor een type gas we hebben. Met deze meting kunnen we constateren of we echt een nieuwe toestand van materie hebben gevonden, het gezochte Bose-Einsteincondensaat, of dat we wellicht alleen maar een klein beetje heel koud gas hebben.

Dipoolval

Onze Magneto-Optical Trap (MOT) uit het tweede deel van deze serie volstaat dus niet meer. De fotonen die we gebruiken om het gas samen te brengen op de gewenste locatie, en om dat gas verder af te koelen, hebben hun limiet bereikt. Het gas is nu zo koud dat elke absorptie van een foton het evenveel verwarmt als afkoelt. Een eenvoudige oplossing voor dit probleem is: doe de lasers uit. We moeten dan natuurlijk wel een nieuwe manier vinden om het gas vast te kunnen houden. Gelukkig hadden we ons monster al op de juiste plek gekregen met behulp van de MOT. Het zou geen probleem moeten zijn om nu gewoon de lasers uit te doen, en dan met alleen magneetvelden het gas te controleren. Dat kan inderdaad, en zo’n constructie heet een magnetische val. Deze methode is betrekkelijk eenvoudig, en ook goedkoop om te bouwen. De val werkt als volgt: vrijwel alle atomen zijn eigenlijk heel kleine magneetjes. Een magneetveld dat de juiste configuratie heeft kan deze kleine magneetjes gemakkelijk vasthouden (laten zweven) op hun huidige plek, precies zoals je dat zou doen met normale magneten. Het grote nadeel van deze methode is echter de benodigde ruimte voor de spoelen die het magneetveld opwekken. Ook moet deze elektronica gekoeld worden, meestal door middel van vloeistofkoeling, wat een lastige opgave kan zijn. Een andere valmethode, die ik hier verder zal toelichten, het de ‘dipoolval’. De dipoolval (of ‘dipole trap’ in het Engels) baseert zich juist op elektrische velden. Specifiek is het idee gebaseerd op het feit dat het veld waarin licht zich voortplant een elektrische veldcomponent heeft. In gewonemensentaal: we gaan alleen lasers gebruiken, want die veroorzaken zelf al een elektrisch veld. Overigens is het in de praktijk vaak zo dat de twee methodes, de magnetische val en de dipoolval, tegelijkertijd toegepast worden, voor maximaal effect.

Het lijkt misschien raar om in het koelproces weer lasers te gebruiken. Hierboven zei ik immers dat de lasers juist niet goed meer waren.: ze verwarmden ons gas immers te veel. Dat klopt inderdaad. Er is alleen een groot verschil: de MOT baseerde zich op absorptie en emissie van fotonen door ons gas. De dipoolval houdt het gas vast door aan onze atomen te ‘trekken’ (of duwen) met het elektrisch veld van de laserstraal. Er worden dus geen fotonen opgenomen of uitgezonden; het effect is niet heel anders dan een negatieve lading die aangetrokken wordt door een positieve lading.

Het elektrisch veld van een laserstraal kan in een atoom een dipool induceren. Je kunt je dat als volgt voorstellen: een atoom bestaat uit een positief geladen atoomkern omgeven door een negatief geladen wolk van elektronen. Het elektrisch veld trekt de kern nu een beetje omhoog uit zijn eventwichtspunt, zoals in afbeelding 1. Dit trekken gebeurt doordat fotonen verstrooien op het atoom: ze gaan een interactie aan. Deze interactie is niet hetzelfde als absorptie en emissie; het is meer iets als het ‘afketsen’ van fotonen op het atoom.

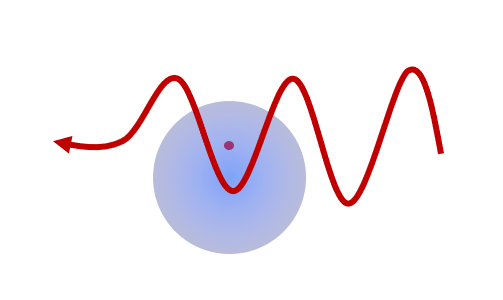
Afbeelding 2. Een dipoolmoment.Een elektrisch veld (rode golf) beïnvloedt een atoomkern (rode punt), en de omringende elektronwolk (blauwe bol), waarbij het een minuscuul elektrisch veld tussen de kern en de wok induceert: een dipoolmoment. Afbeelding: Florian Schreck.

Tegelijkertijd wordt de elektronwolk een beetje omlaag getrokken. Het verplaatsen van de twee elektrisch geladen componenten in verschillende richtingen heeft als effect dat er een minuscuul elektrisch veld ontstaat tussen de atoomkern en de elektronen. Het uiteindelijke gevolg is dat de energie van een atoom een heel klein beetje lager wordt naarmate het elektrisch veld sterker wordt. Aangezien de natuur altijd de energetisch meest gunstige toestand opzoekt, zorgt dit effect ervoor dat het atoom ‘liever in de laserstraal blijft’. We hoeven dus nu alleen ervoor te zorgen dat onze laser op de plekken waar we de atomen willen vasthouden de grootste intensiteit heeft.

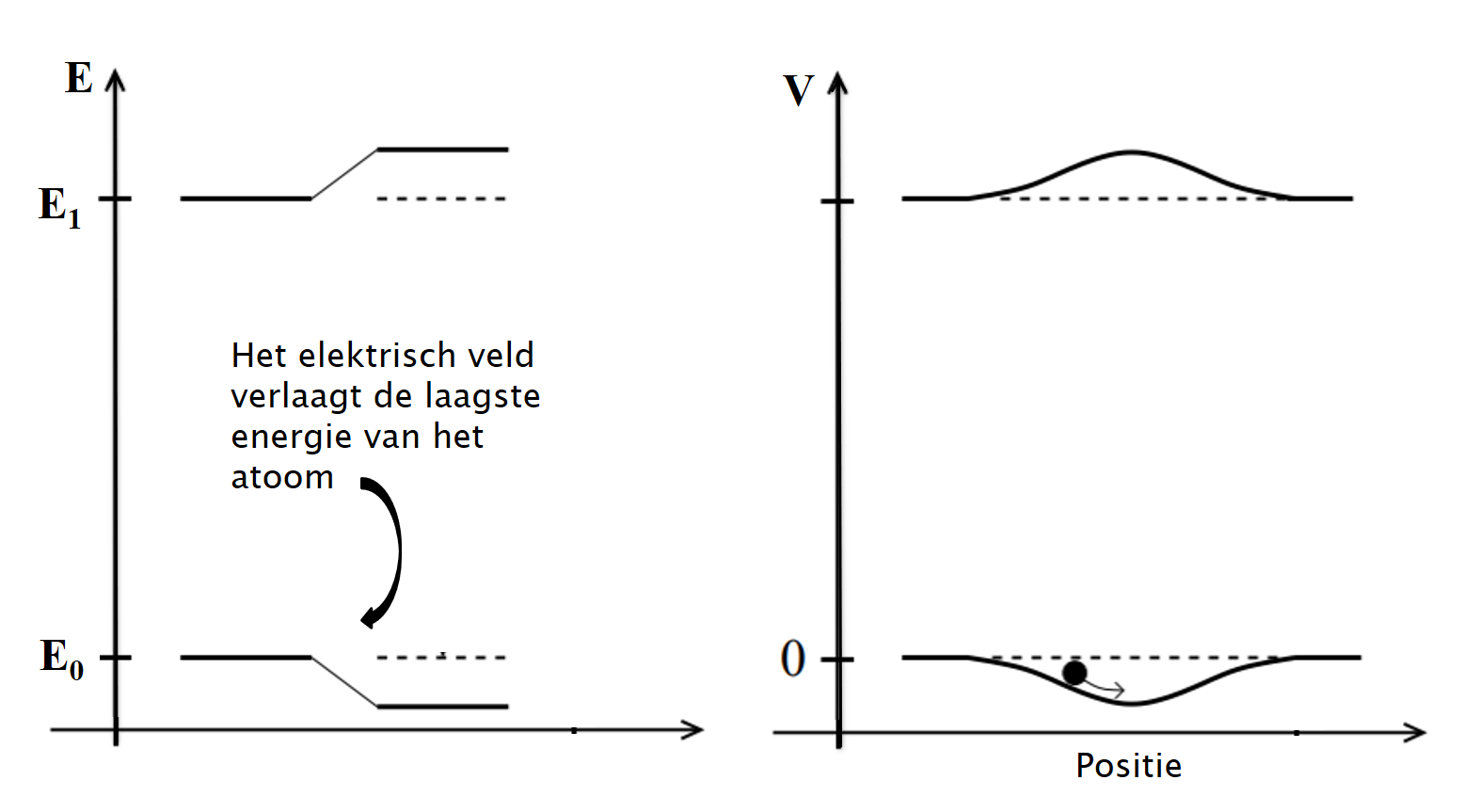
Afbeelding 3. Ontstaan van een potentiaalput.Het elektrisch veld induceert een dipoolmoment in een atoom, wat resulteert in een iets lagere energie van het atoom bij een hoge intensiteit. De linkergrafiek geeft weer wat er gebeurt met de energie. Helemaal links is van het systeem de grondtoestand-energie (de laagste energie), en die van de eerste aangeslagen toestand getekend. Het elektrisch veld verlaagt vervolgens de energie voor de grondtoestand een klein beetje, zoals aangegeven met de pijl. De rechtergrafiek laat het ‘potentiaallandschap’ zien dat een atoom door dit elektrisch veld ervaart. De potentiaalput is dieper waar het licht het meest intens is; daar zullen de atomen zich dus willen bevinden. Afbeelding uit “Optical dipole traps for neutral atoms” van Rudolf Grimm, Matthias Weidemüller en Yurii B. Ovchinnikov.

Samengevat hebben we de volgende situatie: een laserstraal heeft een elektrisch veld. Dat induceert een dipoolmoment in het atoom, waardoor er een ‘potentiaallandschap’ ontstaat waardoor atomen een kracht ondervinden die ervoor zorgt dat ze in het minimum van de potentiaal blijven. Een belangrijk punt daarbij is het volgende. We moeten ervoor zorgen dat ons licht niet per ongeluk tóch geabsorbeerd kan worden door de atomen. De manier om dit te doen, is simpelweg door onze laserstraal op een golflengte te laten schijnen die zeer ver weg ligt van de golflengtes die het atoom zou kunnen absorberen. Dit kunnen we doen door de golflengte van ons licht te verkleinen, of door die te vergroten. Als de golflengte van de laser die we gebruiken voor de dipoolval groter is dan de absorptiegolflengte van het atoom, dan zullen de atomen zich naar de hoogste intensiteit toebewegen. Als de golflengte kleiner is, zal een atoom zich juist weg van de intensiteitsstraal verplaatsen. In afbeelding 3 wordt dit schematisch weergegeven. Door deze twee effecten samen te gebruiken, kan men, met behulp van verschillende laserstralen, de atomen goed manipuleren en mooie dipoolvallen maken.

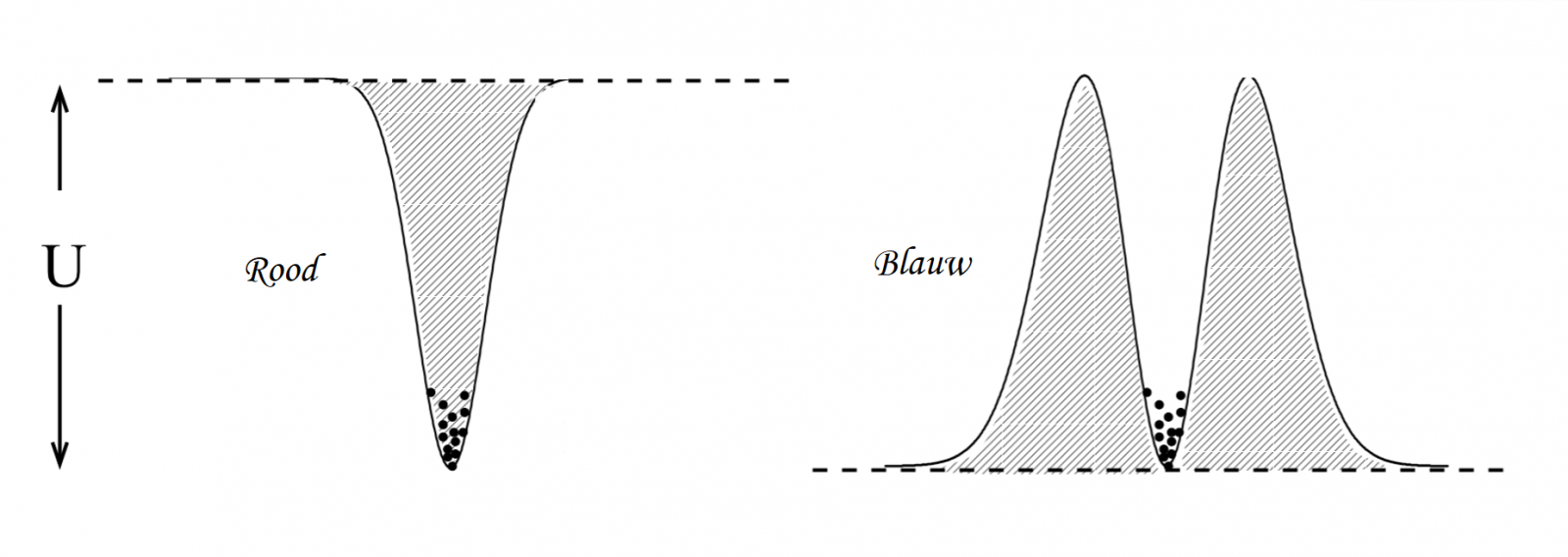
Afbeelding 4. Atomen manipuleren met licht.De twee soorten lichtstralen die we kunnen gebruiken voor een dipoolval. Aan de linkerkant vormt de laserintensiteit een ’klokvorm’. De intensiteit is het grootst in het midden, en neemt exponentieel af naar de zijkanten. Dit is het geval als de golflengte van licht groter is dan de absorptiegolflengte van het atoom (ook wel ‘roodverschoven’ genoemd), waardoor de atomen naar het centrum van de lichtstraal bewegen. De rechtersituatie betreft lichtstralen met een kleinere golflengte. Door in dit geval twee intensiteitspieken te creëren, dwing je de atomen in het gas om tussen de twee pieken in te blijven. Afbeelding uit “Optical dipole traps for neutral atoms” van Rudolf Grimm, Matthias Weidemüller en Yurii B. Ovchinnikov.

Afkoeling door verdampen

De laatste stap die we nemen om ons doel van een ultrakoud gas te bereiken, is die van afkoeling door verdamping. Deze methode is eenvoudig samen te vatten in één zin: Haal continu alle warme atomen weg, en bewaar alleen de koude atomen. De naam van deze techniek wordt hier ook gelijk mee verklaard: we koelen ons gas af door warme atomen te laten verdampen uit ons systeem. Dit is precies de manier waarop een kop koffie afkoelt, trouwens: de stoom voert de heetste moleculen af, en wat er overblijft is kouder.

Dit alles is natuurlijk weer makkelijker gezegd dan gedaan. Hoe selecteer je immers op ‘warme’ en ‘koude’ atomen, en hoe neem je de warme weg? De dipoolval die we hierboven zijn tegengekomen zal hier een cruciale rol in spelen.

Intermezzo: Thermische snelheidsverdeling

Hierboven noemde ik ‘warme’ en ‘koude’ atomen. Dit lijkt tegenstrijdig: het gas dat we gemaakt hebben was toch gewoon op één temperatuur? Zoals je misschien nog weet uit het eerste artikel, heeft temperatuur echter te maken met de ‘gemiddelde kinetische energie per vrijheidsgraad’ van een atoom. Het woord gemiddelde impliceert al dat er in een gas van een bepaalde temperatuur atomen zijn met een hogere energie dan gemiddeld – en natuurlijk ook atomen met een lagere energie. Hogere energie betekent: een hogere snelheid. Als we dus weten hoe de snelheden verdeeld zijn van alle atomen in een gas, kunnen we een grafiek hiervan maken. Deze grafiek heet de thermische snelheidsverdeling, zie afbeelding 4. De verdeling vertelt ons hoeveel atomen hoge en lage snelheid hebben, en dus hoge en lage energie. Alle atomen in ons gas met een hoger dan gemiddelde snelheid noemen we de ‘warme’ atomen, en die met een lagere snelheid ‘koud’.

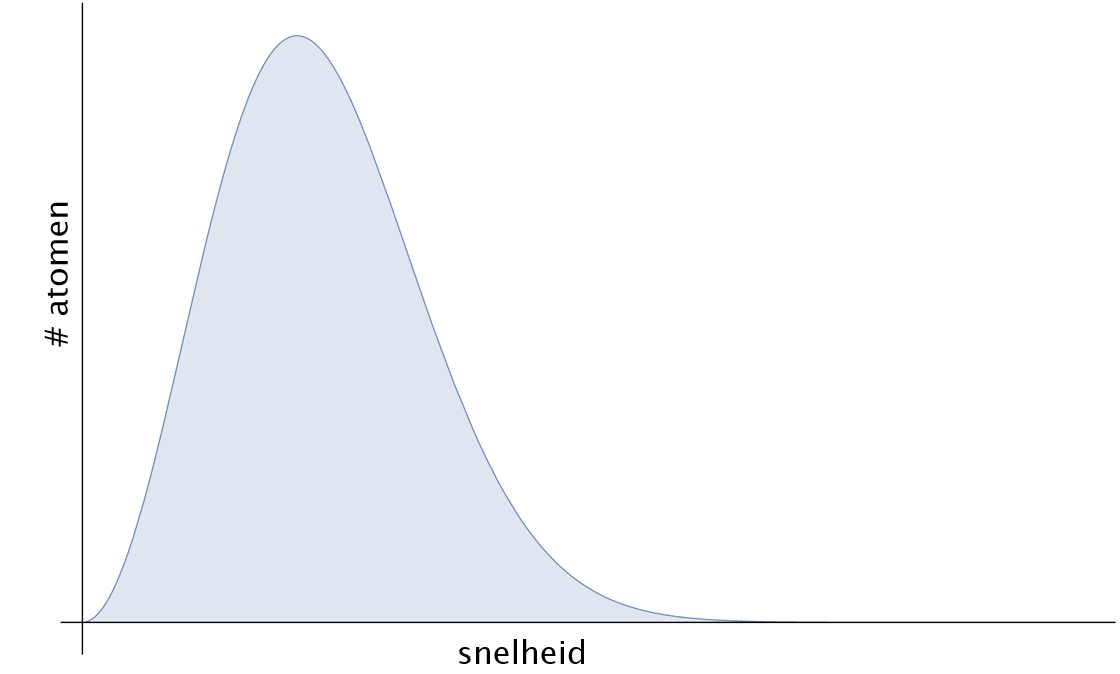
Afbeelding 5. Een thermische snelheidsverdeling.Grafiek van een thermische verdeling in een gas met een bepaalde temperatuur. Deze grafiek geeft de verdeling weer voor wat natuurkundigen een ideaal gas noemen: er is daarin geen interactie tussen verschillende atomen. In de praktijk is dat natuurlijk wel het geval, maar desondanks geeft deze afbeelding een redelijk beeld van hoe de snelheden in een gas verdeeld zijn over de atomen. Afbeelding: Lieuwe Bakker.

Hoe selecteer je ne op warme en koude atomen? De warme atomen zijn zoals je in het intermezzo hierboven kunt lezen niets anders dan die atomen die zich met een hoge relatieve snelheid bewegen. Afbeelding 5 geeft een stapsgewijze weergave van het nu volgende afkoelproces.

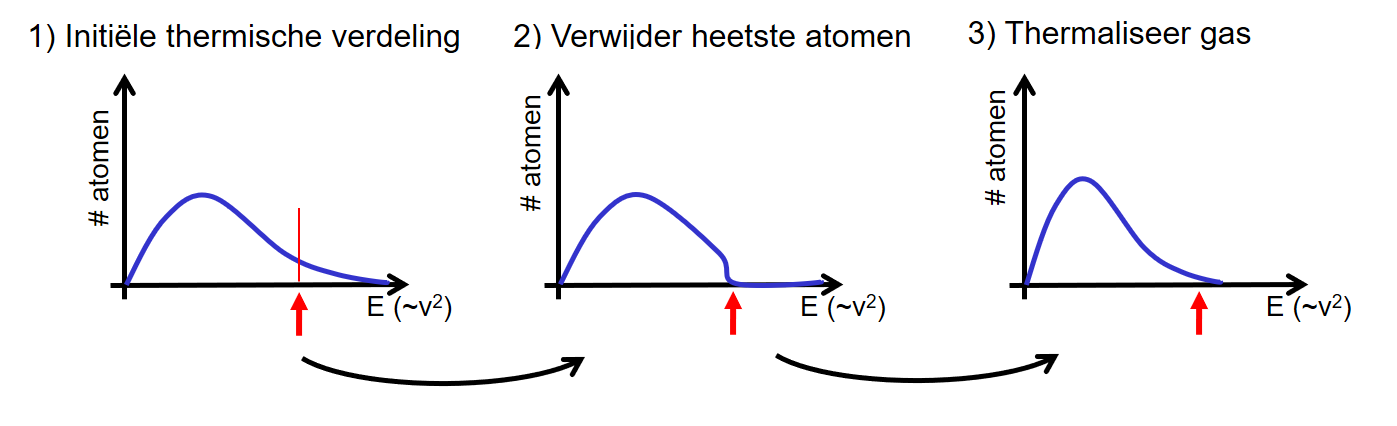
Afbeelding 6. Afkoelen door verdampen.In stap 1 beginnen we met een gas op een bepaalde temperatuur met een bijbehorende snelheidsverdeling. We ‘snijden’ alle atomen met een hoge snelheid, alle atomen rechts van de rode pijl, in stap 2 weg. Vervolgens wachten we eventjes om de overgebleven atomen te laten ‘thermaliseren’. Dat betekent dat we wachten tot ons gas na de nodige botsingen tussen de overgebleven atomen weer een snelheidsverdeling heeft die lijkt op de verdeling in stap 1, maar dan natuurlijk met een gemiddeld lagere temperatuur. Dit is te zien als het verschuiven van de top van de verdeling in de grafiek. In stap 3 is de top meer naar links geschoven dan in stap 1: de meeste atomen hebben een lagere snelheid gekregen, en dus is het gas op een lagere temperatuur gekomen. Afbeelding: Florian Schreck.

Natuurlijk moeten we op de een of ander manier deze snel bewegende atomen zien uit te filteren. Dit kunnen we doen met behulp van onze dipoolval. Het is namelijk zo, dat de intensiteit van het gebruikte licht in die val bepaalt hoe diep de potentiaalput is. Hoe dieper een potentiaalput, hoe meer kinetische energie er nodig is om te kunnen ontsnappen. Het selectieproces is dus simpel: verlaag de intensiteit van de laser geleidelijk. Dit is eenvoudig te doen door minder vermogen uit de laser te laten komen, een kwestie van ‘draaien aan de knop’. Eindelijk eens iets wat we gemakkelijk kunnen bewerkstelligen! Deze methode is alleen niet perfect: we ‘verdampen’ een deel van ons gas, en verliezen dus atomen. We moeten oppassen dat we uiteindelijk nog genoeg atomen overhouden om iets nuttigs mee te kunnen doen. Een gas van een handjevol atomen is immers nauwelijks meer een gas te noemen.

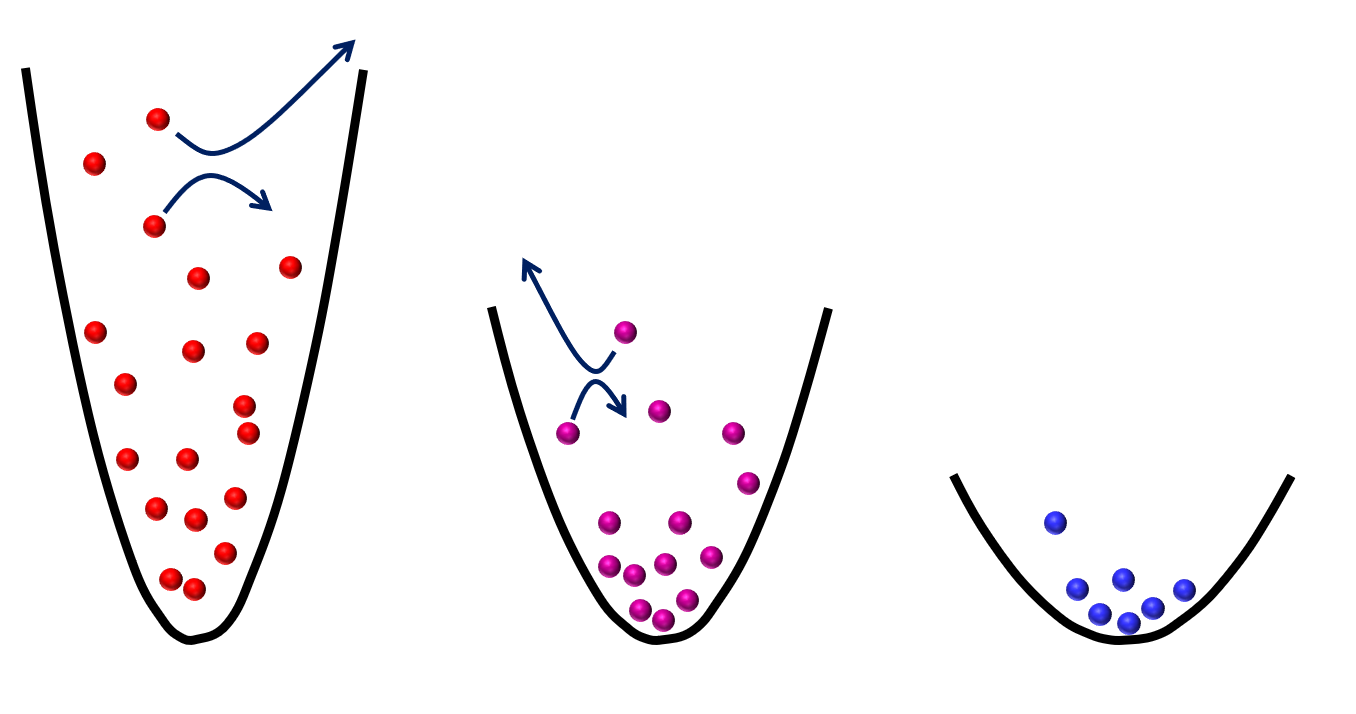
Afbeelding 7. Afkoelen door verdampen.Schematische weergave van het afkoelproces door verdampen. We beginnen met veel atomen in een diepe val. We verlagen vervolgens langzamerhand de potentiaaldiepte, waardoor warme atomen verdwijnen (letterlijk wegvliegen!) uit het gas. Door dit proces te herhalen, blijven uiteindelijk alleen de langzaamste atomen over, en is ons gas zeer koud. Afbeelding: Florian Schreck.

Na het laten verdampen van de warme atomen uit het gas, hebben we ons doel bereikt: we hebben een gas met een ultrakoude temperatuur van enkele (honderden) nanokelvins bereikt. Nu moeten we nog op de een of andere manier een meting doen om te zien wat er met ons gas is gebeurd: is het een Bose-Einsteincondensaat geworden? Of een ander exotisch materiaal, zoals een supervloeistof? Misschien is er ook wel helemaal niets gebeurd, en hebben we een ‘normaal’, zij het zeer koud gas.

Metingen doen

Om erachter te komen wat er met ons gas gebeurd is, moeten we een meting doen. Vrijwel elke meting die gedaan wordt aan ultrakoude gassen (en quantummechanische objecten in algemeen) is destructief. Dat betekent dat we slechts één keer een meting kunnen doen, en dat erna het gas zijn gunstige eigenschappen kwijt is. Dit is eigenlijk vrij logisch als je kijkt naar hoe zo’n meting werkt: we beschijnen ons gas bijvoorbeeld met een lichtstraal, en nemen de ‘schaduw’ waar. Je krijgt echter alleen een dergelijke schaduw als het gas een interactie aangaat met het licht. Het licht wat nodig is om deze schaduw te meten is vaak dusdanig energetisch dat het ons gas vernietigt (opwarmt). Ook is er nog een ander detail: meestal willen we in experimenten kijken naar veranderingen binnen een gas. Bij Bose-Einsteincondensaten gaat het dan veelal om de expansiesnelheid van een gas. Om zo’n verandering te meten, moet je het gas wel loslaten om ‘zelfstandig’ een verandering teweeg te brengen. Dit betekent dat men de vallen waarmee het gas wordt vastgehouden moet uitzetten, waardoor het gas uiteindelijk simpelweg wegvliegt.

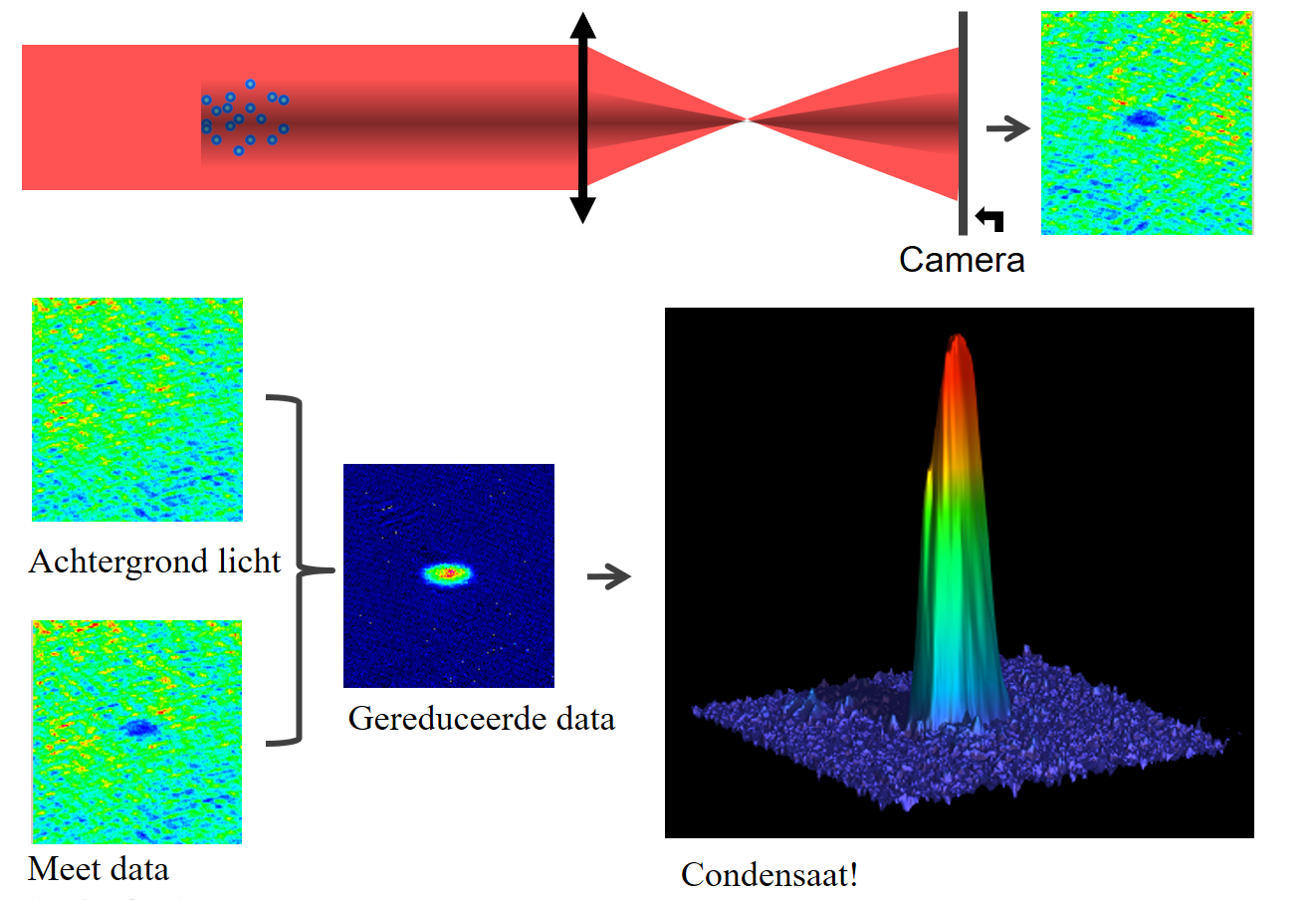
Afbeelding 8. Een meting.Schematische weergave van een meting. Er wordt van links licht geschenen, dat tegen het gas aankomt. Dit gas absorbeert een deel van het licht, afhankelijk van zijn dichtheid. De foto van het resulterende licht wordt verwerkt, samen met een foto van het achtergrondlicht, tot de gereduceerde data, waar we een 3-d plot van de intensiteit van kunnen maken. De hoogte van de piek komt daarin overeen met de dichtheid van het gas. De scherpte van de piek vertelt ons in dit voorbeeld dat we te maken hebben met een Bose-Einsteincondensaat. Afbeelding: Florian Schreck.

Onze meting resulteert letterlijk in een foto van een schaduw. Door deze foto te vergelijken met een soortgelijke foto zónder schaduw (dus: zonder gas), kunnen we reconstrueren wat de dichtheid van het gas was op elk punt. Deze dichtheidsverdeling kan ons iets vertellen over het gas: een Bose-Einsteincondensaat bestaat uit deeltjes die heel ‘dicht op elkaar zitten’ en heeft daarmee een heel ander dichtheidsprofiel dan een normaal koud gas. Sterker nog: een Bose-Einsteincondensaat heeft een uniek dichtheidsprofiel. Vergelijkbare methodes kunnen worden toegepast om supervloeistoffen en andere exotische fases van materie waar te nemen.

Experimenten met koude gassen en onderzoek naar koeltechnieken hebben in de loop van de 20^e eeuw geleid tot vele belangrijke ontdekkingen. De eerste supergeleiders en supervloeistoffen werden geïdentificeerd. Supergeleiders zijn tegenwoordig ook niet meer weg te denken uit de natuurkunde, en zijn zelfs van fundamenteel belang in moderne experimenten zoals in de deeltjesversneller op het CERN of in het ITER-kernfusieproject. Ook Bose-Einsteincondensaten waren een belangrijk middel om de theorie van de quantummechanica te testen in een laboratorium. Vandaag de dag wordt er nog steeds gezocht naar nieuwe toepassingen van koude gassen. Een wat moderner voorbeeld is dat van ultra-precieze klokken, die gebruikt worden door bijvoorbeeld navigatiesatellieten. En als toepassing van een Bose-Einsteincondensaat zou je bijvoorbeeld kunnen denken aan een laserstraal van materie! Die zou potentieel gebruikt kunnen worden om zeer hoogenergetische ‘lasers’ te ontwikkelen, wat vele toepassingen zou kunnen hebben in industrie. Tot rond de kerst van 2019 leek een dergelijke laser een toekomstdroom: het lukte onderzoekers maar niet om een Bose-Einsteincondensaat te creëren en vervolgens lang stabiel te houden, wat juist nodig is voor praktische toepassingen. In de loop van de tijd ‘verdampten’ atomen steeds door toevalsprocessen die niet perfect weggefilterd kunnen worden. Daar kwam verandering in toen Florian Schreck, onderzoeker aan de UvA, met zijn onderzoeksgroep als eerste ter wereld erin slaagde om een ‘steady state Bose-Einsteincondensaat’ te maken. Dat heeft hij voor elkaar gekregen door een constante toevoer van nieuwe ultrakoude atomen te realiseren, om zo het langzaam verdampende condensaat continu aan te vullen. Dit proces is nog beduidend ingewikkelder dan alleen wat ik heb kunnen beschrijven in deze serie over koude gassen, maar desondanks zijn de meeste belangrijke concepten en technieken die in zulk modern onderzoek gebruikt worden wel aan bod gekomen.

Doorbraken als deze tonen aan dat er heel veel gebeurt in het moderne onderzoek naar koude atomen, en dat we in de komende jaren ook nog heel wat van dit vakgebied kunnen verwachten!

Een belangrijke bron voor dit artikel was Optical dipole traps for neutral atoms van Rudolf Grimm, Matthias Weidemüller en Yurii B. Ovchinnikov.