
F=ma. It’s the one equation most people seem to remember from their high school physics classes. That is no coincidence: it is a beautifully small equation that captures most of our everyday life.
At every point in time we can look at the position and velocity of an object and, with the knowledge of the forces acting on that object at that instance, compute its future trajectory via the small equation \( F=ma \)! Just like a movie where the motion of objects comes to life by having many frames per second, Newton’s second law manages to trace out trajectories. It computes the forces at each point in time and updates the motion of the particle accordingly.
We come to one obvious problem with the equation \( F = ma \): what happens for objects like light that have \( m=0 \)? Does the vanishing mass mean that forces can never pull or push light? This cannot be the case as we know that the gravitational force can deflect light. This is an underlying issue with Newton’s second law; it is not a general law that can be applied to any object.
As so often in science, we therefore try to find patterns between phenomena and try to understand them, hence, under the umbrella of a more fundamental set of laws. The mathematician Joseph-Louis Lagrange was thinking about the patterns underlying each path that any object would take. The way he accomplished to say something useful about those patterns was by defining a new mathematical tool now famously known as the Lagrangian \( L \) of a system. It is computed from the kinetic energy \( T \) and the potential energy \( V \) of an object, in the following way
\( L(x(t),\dot{x}(t))=T-V \),
where
- \( x(t), \dot{x}(t) \) are the position and velocity respectively and
- \( t \) is the time coordinate.
Physically, the Lagrangian describes the transfer of energy between the two types of energy1: potential and kinetic. For example, you can think of an object falling from some height: the initial potential energy will be transformed into kinetic energy as the object is falling. So we exchange the energy corresponding to location for one corresponding to velocity and vice versa.
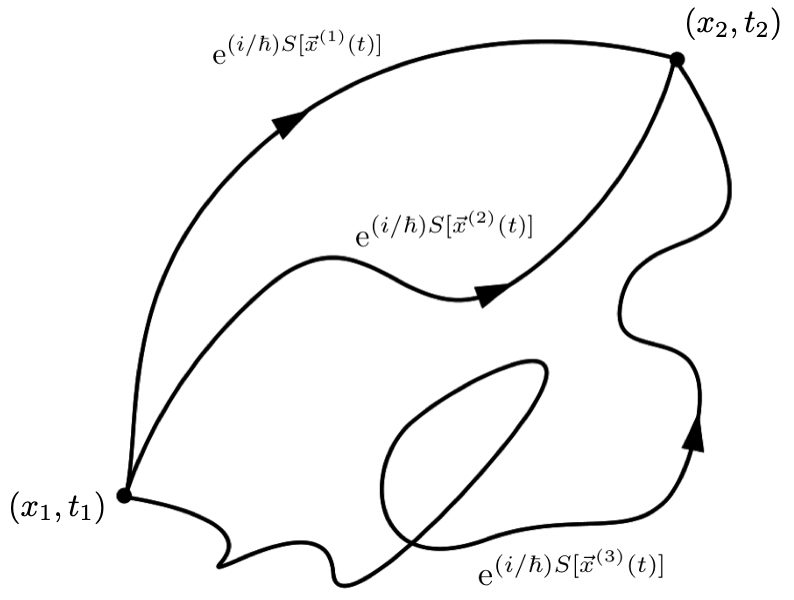
The next insight lies in the fact that, roughly speaking, the universe is lazy. It wants to do as little as possible over time. ‘Doing something’ physically means that there is a transfer of energy, as this results in dynamical processes. Let’s try to formulate this mathematically. We want to define something that encapsulates the transfer of energy over time. For that we use the Lagrangian and integrate it over all possible times \( t \). This motivates us to define a mathematical tool, called the action \( S \):
\( S[x(t)]=\int_{t_1}^{t_2} \; L(x(t),\dot{x}(t)) dt \).
Using the ‘principle of universal laziness’2 we will find the path \( x(t) \) that minimizes the action
\( \delta S[x(t)]=0 \).
Here the symbol \( \delta \) means that we look at changes in the action, so we look for the minimum of the action as a function of the path. This will constitute the most ‘lazy’ path. Therefore the action, compared to Newton’s second law, is not a cause-effect law whereby one computes every frame of the trajectory and sews them together. It probes all possible paths and picks out the one with least action.
Indeed one can find such a path from the action through the Euler-Lagrange equation1:
\( \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{x}} \right) – \left(\frac{\partial L}{\partial x} \right) =0 \).
This equation may look rather scary and not easy to solve, but we won’t ask you to – it’s just important to know that such an equation exists, and that therefore problems defined by a Lagrangian have a perfectly well-defined solution.
Summarizing: the Lagrangian formalism allows us to define the motion of an object independent of what type of object it is – even massless light. It relies on the fact that all paths that objects actually take share the same pattern: they minimize the action. Much later, this key insight even allowed physicists to describe situations where quantum mechanics and relativity are present, making the Lagrangian and the action very powerful tools!
[1] Of course you might have heard of many other ‘types’ of energy like thermal energy, chemical energy, gravitational energy, et cetera. But all of them rely on the fundamental ingredients of the position and velocity any object may have, hence we only require potential and kinetic energy. For instance, thermal energy can be thought of as the average kinetic energy.
[2] Of course this has a proper name in physics and goes under the name of principle of least action.
[3] One can actually derive the Euler-Lagrange equation via the principle of least action, but this would take a full course in calculus to derive. Feel free to still look it up!