
Curious Ants and the Harmonic Series
Imagine an incredibly specific setup: we find ourselves with a rubber rope of length \( x_0 \) and an ant sitting on one end of the rope. The ant has the dream of reaching the other end at some point in its lifetime. Fortunately, it is capable of moving a distance \( x_\text{Ant} \) per second; unfortunately, the rope (through some dark magic) starts to stretch out with a constant distance of \( v \) units per second. If we start out with \( x_0 = 1 \text{km} \), \( v= 1\text{km/s} \), and \( x_\text{Ant} = 1 \text{cm} \) each second we can ask the question: Does the ant ever reach the other end of the rope? The answer is surprisingly: yes!
To illuminate this mystery, we will first argue from an intuitive perspective, and then try to verify our intuition rigorously via the so-called harmonic series.
The crucial ingredient in understanding this paradoxical result is to think about the fraction of rope traveled. Namely, we will focus on the ratio of distance traveled by the ant in each one-second interval with respect to the current (stretched-out) length of the rubber rope. The expression describing this ratio is
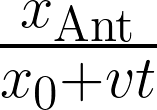
which represents the fraction of rope traveled in the second occurring at a specific time \( t \). The total ratio of distance traveled after \( T \) seconds is then given by the sum
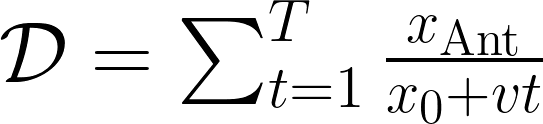
Now, as we are dealing with ratios, when at some time T this number \( \mathcal{D} \) surpasses 1, then we know that the ant has reached the other side of the rope! For simplicity, imagine that the ant starts out in the center of the rope and that the ant does not move in the first second. Pictorially, this looks as follows
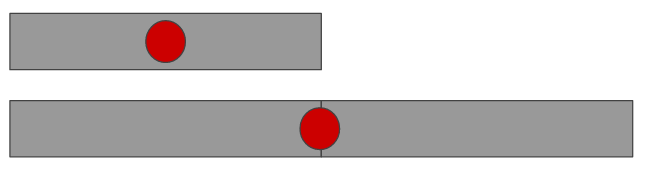
Clearly, the ant (illustrated as a red dot) is still in the center, meaning at the halfway point of the rope. If the ant were then to just move a bit after the first second
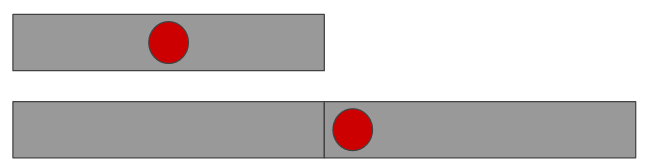
it would undoubtedly make progress! Intuitively, this is because as the rope stretches, there is, not only more ‘space’ in front of the ant but the same extra amount behind it, as the entire rope stretches homogeneously. This gives us some intuition for how the ant can reach the other side of the rope, even though the rope is stretching in a uniform manner after each step it takes. No matter how tiny the ant’s distance per second and how long the rope is, the ant will eventually reach the end.
Mathematically, the reason for this result is equally impressive. The fraction of the rope traveled can be written in terms of the harmonic series
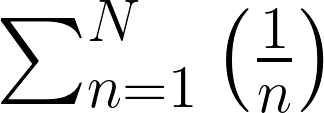
a sum that formally goes to infinity as the number \( N \) goes to infinity as well. Keeping this in mind, we can bound the fraction of rope that the ant travels by introducing a \( t \) as follows
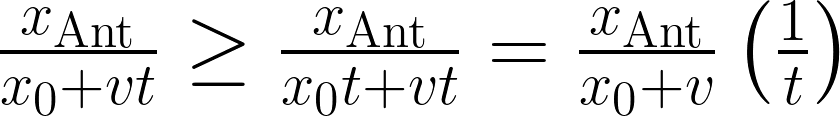
This trick allows us to compare the harmonic series with our sum for the total fraction of the rope traveled \( \mathcal{D} \). Mathematicians, very cleverly, call this a comparison test. In our case, the comparison test allows us to get a lower bound on the total fraction of rope traveled.
We can now take the full sum and, as the harmonic series diverges, we will find a value of \( T \) at which the fraction of rope traveled will undoubtedly have reached 1 which hence indicates that the ant has, indeed, completed its quest towards the end of the rope. Sadly, the ant will not reach its quest in its lifetime, because the total time \( T \) of the trajectory, for the values above, is approximately
![]()
seconds. Just to give an indication of how to think of this number: the age of the observable universe is around \( 10^{17} \) seconds. To put it in a nutshell, rigorously it is possible, but practically never happens, to reach the other end.
Astrophysical Acceleration
If we now think of the rubber rope as our universe, expanding in a uniform matter, we may think that this, even though unpractical, result would mean that all stars in our universe will never be completely hidden and that if we wanted to, and lived forever, we could actually reach the edge of the universe and find out what lies beyond! Right? Well, actually – apart from the possibility that the universe may be infinite in size to begin with – there is a small caveat that makes this argument fail in our universe. The decisive difference is that our universe does not expand in a uniform manner during each time step. Rather, its expansion is accelerating! This acceleration makes the length of the rope, and analogously the distance to the edge of the universe, stretch more after each second and so makes the journey to the other end of the rope (that is, the universe) impossible!1
All in all, we have seen that our ambitious ant allows us to access the astrophysical acceleration of our universe. Hard work and a 43429-digit number of seconds will make almost anything possible. That is, as long as the edge of the universe does not keep running away from us at an ever-increasing speed.
[1] This, of course, depends again on all the values above, but those now include the acceleration. There are certainly specific (low) values for the acceleration, where the ant still remains victorious in its quest to reach the edge of its universe.