
The event horizon also provides a conundrum. By studying quantum fields in a black hole background, Stephen Hawking found that black holes radiate particles from the perspective of an accelerated or asymptotic observer. ‘Asymptotic’ means that he or she sits virtually infinitely far away from the black hole horizon. Hawking’s results raise an important question: how can the black hole radiate if the black hole horizon itself is just an ‘empty’ region of spacetime?
In the following, we will understand this apparent paradox and relate it to near-horizon geometry. In the process, we will also find instructions for how to build near-horizon regions yourself at home!
The relativity of Hawking radiation
The usual explanation for Hawking radiation is that particle-antiparticle pairs are created in the intense sea of fluctuations of the quantum fields near the black hole’s horizon. The story goes that one particle falls into the black hole and the other escapes it just barely, which is the radiation we see from an outsider’s perspective.
This is a very neat description, which Hawking himself also used to describe his discovery. However, it is not the full story (as Hawking was of course very much aware). Hawking radiation is very much connected to the fluctuations of the quantum fields, but with a slight nuance that comes from our good friend Albert Einstein. In particular, the existence of Hawking radiation is related to the very notion of relativity. Let me explain how.
For simplicity, we will just imagine a stationary observer in empty space. This observer is surrounded by the quantum mechanical fluctuations of the quantum fields; these fluctuations usually remain pretty much stable, in the sense that one will not see a real particle permanently emerging out of nothing. In particular, the quantum field jiggles around with positive and negative frequency waves, which cancel out in the vacuum; a real particle, instead, would be an oscillation that does not get canceled out.
Back to our black hole: an observer that falls into the black hole moves on a geodesic – the equivalent of a straight path in curved space-time – and hence will, from his or her point of view, not distinguish locally between the black hole horizon and empty space. As a result, he or she does not see Hawking radiation, which contradicts the naive picture of particle-antiparticle pairs. It is, nevertheless, the case that an observer hovering above the horizon will see a spectrum of Hawking radiation. This effect is purely due to the fact that an observer hovering above the horizon needs to accelerate to not fall into the black hole; this is not a geodesic observer.
Roughly speaking, the reason why an accelerated observer sees Hawking radiation is that he or she disagrees with the fact that the positive and negative frequency waves cancel. In fact, such an observer does indeed see a bath of particles! As is well known, in relativity observers do not need to agree on specific physical quantities. It turns out that accelerated observers do not even agree on the energy, and hence frequency, of the quantum fluctuations! Because of the gravitational pull of the black hole, and the subsequent necessary acceleration to hover above the horizon, we can mathematically prove that there needs to be an associated spectrum of particles, the Hawking particles. The Hawking particles are at a particular temperature, the Hawking temperature, which depends crucially on the characteristics of the black hole.
In the next section, we will analyze the black hole features giving rise to these Hawking particles, and introduce the tools to create your very own black hole horizon at home!
Assembly instructions for horizon geometry
Interestingly, the Hawking temperature can be derived by looking only at the near-horizon geometry of the black hole. It turns out that one can use a simple relation between the quantum-mechanical point of view and one more familiar from the theory of thermodynamics. That relation requires us to treat time as a periodic variable, similar to a unit circle with a periodicity of 2.
In order to study such a ‘compactified’ time coordinate and its relation to the thermodynamic properties of black holes, one needs to approach the horizon and look at the local geometry there. It turns out that here, the local geometry looks quite odd. It seems like the time circle we expected to have has an angular deficit, i.e. it is not periodic with the same period of 2 that we set it up to have in the ordinary space-time away from the black hole.
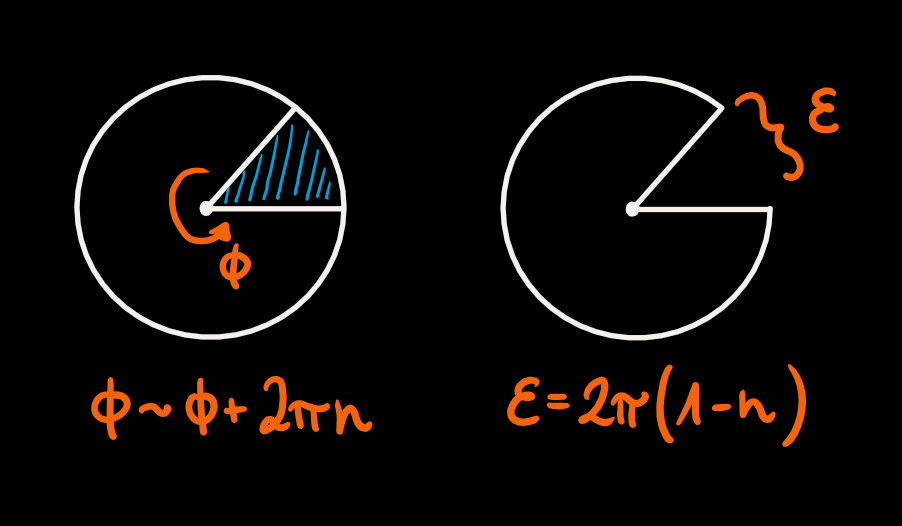
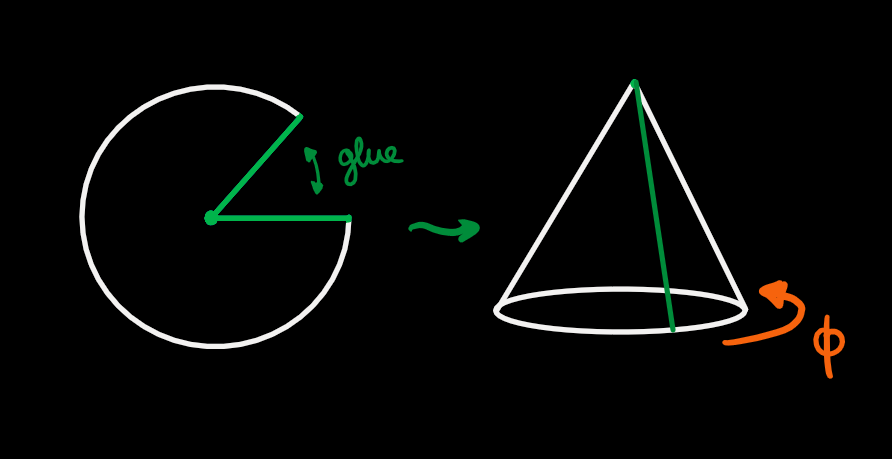
The so-called angular deficit – the ratio between the missing part of the period and the full expected period of 2 – often labeled by n, is a number smaller or equal to 1 and depends crucially on the Hawking temperature. Now why is this different period of the time circle so important? Well, when you take concentric circles of length 2 (or in old-fashioned terminology: 360 degrees) they simply fill up a plane. If you take circles of length less than 2, you can still put them together, but now they form a cone! That is, if we glue the cut-out parts in the image above together, we find that there is a conical singularity, which is the pointy piece of the geometry.
This conical singularity is unphysical, as from Einstein’s theory we expect space and time to be smooth! (Note that what we are describing here is not the spacetime singularity at the center of the black hole.) The resolution to this problem is that we need to fix the periodicity of the compactified time coordinate by hand. Now recall that this period was related to the temperature – in fact, we need it to be exactly given by the (inverse) Hawking temperature, which fixes n = 1, and hence there is no longer any angular deficit, yielding a smooth spacetime. This is flabbergasting: by looking at the near-horizon geometry we could tell what the Hawking temperature needed to be in order to have a smooth spacetime.
Try this at home: take a piece of paper and cut out a disk, followed by cutting out a little triangle from the disk to get an angular deficit. See the above figures. Then stick the two ‘ends’ together and, voilà, you have built a black hole conical singularity! Now try it out for different angular deficits and see what you get. If you do not want a singularity, there is only one thing you can do: not cut at all!
Conical singularities and beyond
As we have seen above, conical singularities seem to indicate that there is a precise thermodynamic interpretation for black holes originating from their near-horizon geometry. Even if this picture is complete, there remain some open questions, especially concerning the geometries with multiple conical singularities.
Research shows that one can indeed include multiple conical singularities in a single space-time, and still get a finite answer for thermodynamic properties like entropy. In the case of only one singularity, we saw that these thermodynamic properties were related to quantum properties such as Hawking radiation. However, in the multiple singularity case, the connection with quantum-mechanical fluctuations of spacetime is hardly understood.
To put it in a nutshell, conical singularities are intricately connected to black holes and their thermodynamic properties, but more research on their quantum properties needs to be done to fully shine a light in the dark abyss that hopefully one day will be a complete theory of quantum gravity.