
Coherent quantum information
Emergent quantum technologies, such as quantum computing1, quantum communication, and quantum sensing, require precise engineering of specific quantum states (that is, specific quantum mechanical configurations of a system) to harness the advantages that quantum mechanics offers, like superposition and entanglement.
In all quantum systems, one encounters dense energy spectra – the different states have energies that are very close together – which makes the navigation through these landscapes, and therefore the ability to target special quantum states, very difficult. The navigation is controlled by external fields that alter the properties of the quantum system under inspection. For instance, one can control the spin of an electron by applying magnetic fields to perform quantum gates for quantum computers – see the figure below.
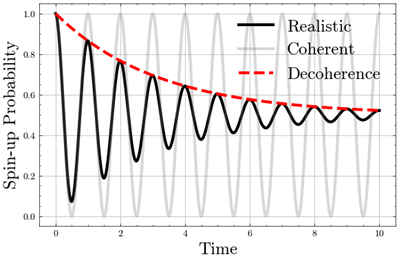
However, during the operation, many errors can occur, leading to a loss of quantum information, a phenomenon called decoherence. This makes the control of quantum information the cornerstone in the development and implementation of practical quantum technologies.
Optimal quantum control
To surpass this challenge, researchers employ techniques from optimal control theory. In the context of quantum physics, this refers to the shaping of the external fields to engineer the interactions that give rise to the target state after some operation time. One subset of these techniques is called shortcuts-to-adiabaticity, where the goal is to remain on a specific branch of the energy spectrum and suppress any jumps to higher (or lower) energy states. An oversimplified, yet helpful, analogy is that of driving a car at high speeds on a serpentine road. Staying on the energy branch translates to remaining on the road, without deviating from it (quantum jumps to higher/lower energies). The goal of optimal control is to adjust the speed of the car over time and to step off the accelerator when the serpentine road has a drastic change of direction.
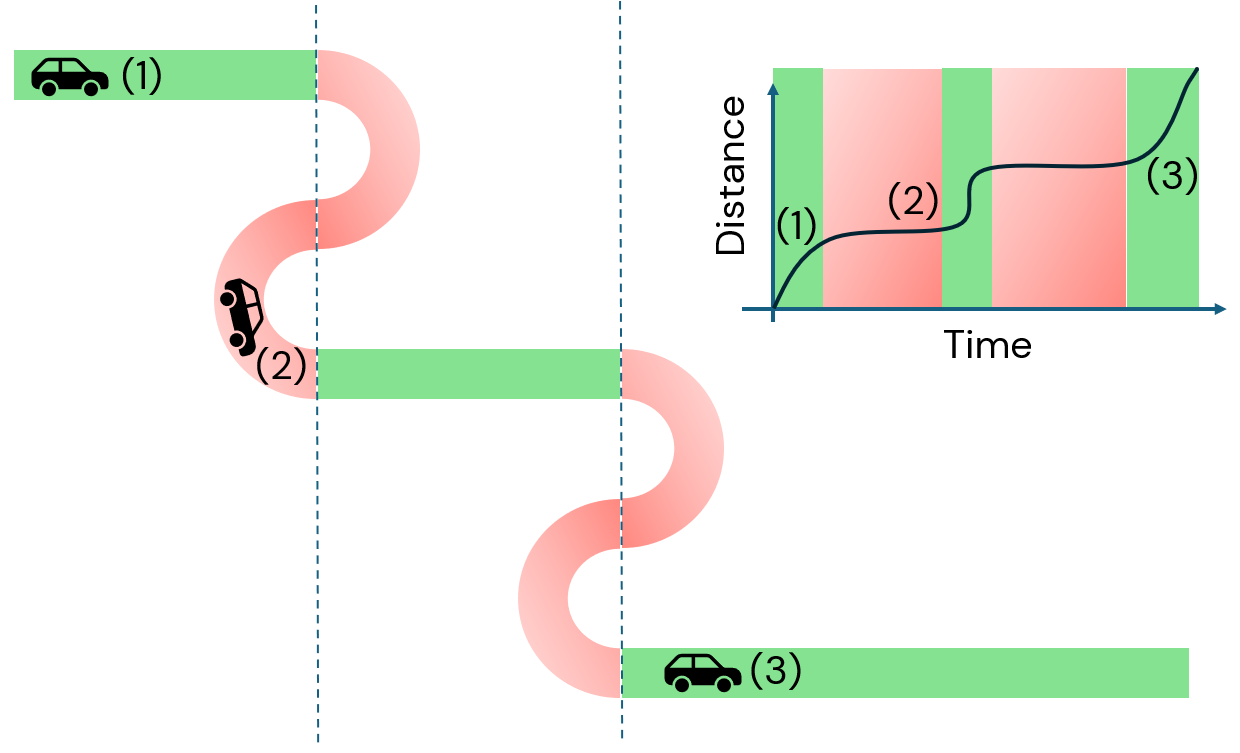
The biggest question in optimal control theory is: How can we implement these optimal strategies?
Quantum geometry for optimal control
Despite many decades of research, new and innovative approaches for optimal control are still being explored by researchers. A fascinating route, particularly in the context of quantum optimal control, is a duality that exists between optimal adiabatic control and geometric structures. In essence, the complicated task of exploring all possible adiabatic strategies can be described by a geometric picture2. In this framework, one describes the engineering from one initial quantum state to the final target quantum state by the motion of a point whose coordinates are determined by the control fields (for instance, different magnetic field directions, or voltages) through a curved geometry, whose dimension only grows with the number of different control fields (critically, it does not scale exponentially as one is used to in quantum systems).
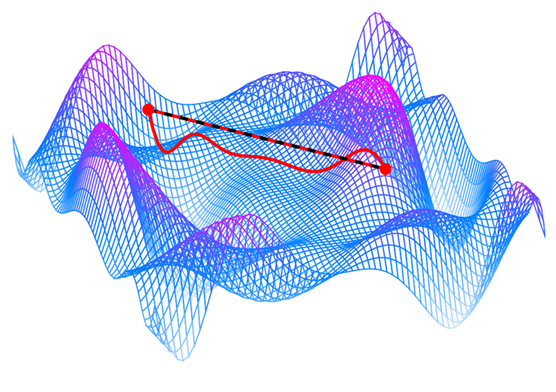
Moreover, the astonishing duality also allows us to enforce these optimal strategies by finding the shortest path between the initial configuration of control fields and the target configuration.
This geometric duality between the complicated energy landscape of the quantum system and the control field landscape allows us to pursue the safest (and fastest) drive of our lives on a road dictated by the wish to engineer precise quantum states efficiently.
[1] For a recent introductory article see Computing: from classical to quantum (1) | the Quantum Universe and Computing: from classical to quantum (2) | the Quantum Universe
[2] For more math-heavy details: [2409.03084] Quantum geometric protocols for fast high-fidelity adiabatic state transfer