
Dark matter is one of the most elusive substances in the Universe. While the evidence for its existence is plentiful, it has only ever revealed its presence through gravitational interactions with ordinary matter. Gravitational interactions between individual particles are effectively impossible to measure, however, owing to gravity’s incredibly weak nature: the gravitational attraction between two protons is 1036 times smaller than their electromagnetic repulsion. For gravity to have a significant effect, we thus need objects that contain a lot of mass. This can easily be achieved by ordinary (baryonic) matter, as it interacts electromagnetically and can thus clump together.
Most models for dark matter assume it to be collisionless, however, preventing dark matter particles from easily losing energy through interactions and clumping together. As a result, dark matter is relatively dilute and dominates the gravitational potential only on large enough scales. As an example: approximately 100% of the mass in the Solar System is baryonic, while baryonic matter only makes up 10% of the total mass of the Milky Way.
There is however a way for gravity to impact systems without needing extreme total masses, namely through dynamical friction. Dynamical friction can be thought of as the gravitational equivalent of air resistance. As you fall through the air (which is generally inadvisable but does make for an engaging thought experiment), the molecules of your skin repulse the air molecules and exchange energy, slowing you down – or at least: decreasing your acceleration – while pushing the air molecules out of your way.
Dynamical friction operates similarly, but the mechanism is inverted, as gravity is a purely attractive force. A massive object moving through a cloud of particles pulls them towards itself, again exchanging energy and slowing down. This is a well-known effect, and it plays an important role in processes like the formation of planetary systems and galaxy mergers. In both cases, the cloud that creates the drag force is made of baryonic matter: gas particles in the former case, and actual stars in the latter. So, while the total gravitational potential is dominated by dark matter during galaxy mergers, it is the interaction between stars that actually defines the final result.
Let us now devise a system where dark matter is a sub-dominant component, but still dense enough to make its presence known through dynamical friction. If we can then predict the main dynamics of such a system from known physics, we could extract dark matter information from the details. The easiest systems to make predictions for are two-body systems, and coincidentally we have recently gained access to a new type of observation of two-body systems in the strong-gravity regime: mergers between binary black holes. As the two black holes spiral around each other, they emit gravitational waves. These waves carry away energy, causing the black holes to slow down and spiral towards each other, before ultimately merging together and forming one larger black hole. If such an inspiral were to happen within a dense dark matter environment, then the dynamical friction exerted by the dark matter could cause the black holes to lose additional energy, speeding up the inspiral. This would in turn change the form of the gravitational wave, an effect known as dephasing, as the gravitational wave desynchronises with respect to the vacuum case.
If we can detect this dephasing, then we can access much smaller scales than with current dark matter observations, opening up a new window into dark matter dynamics. There are two main challenges that a binary black hole system embedded in a dark matter halo must overcome in order for the dephasing to be detectable: the dark matter halo must be dense enough to cause significant dynamical friction, and it must also not get torn apart during the inspiral as the black holes inject energy into the halo. The second condition can be satisfied in an extreme mass-ratio inspiral (EMRI), where one black hole is much, much heavier than the other. The heavy central black hole then leaves the halo undisturbed as it is approximately stationary, while the light secondary black hole cannot scatter large amounts of dark matter particles, keeping the halo roughly intact.
This leaves us with the density requirement. Intuitively speaking, you could imagine that dark matter automatically concentrates around the central massive black hole, due to its strong gravitational attraction, as the black hole moves through space. This is however a very small effect, as dark matter has no effective ways of losing energy and is thus much more likely to simply pass by the black hole and continue on its merry way. Instead, dark matter concentrates when an external gravitational potential is deepening, such as during the growth of a central object. The orbits of the dark matter particles adjust as the potential changes, focusing them towards the centre of mass.
This effect was first studied in the context of WIMPs (weakly-interacting massive particles), a class of dark matter candidate particles that self-annihilate. The original study by Paolo Gondolo and Joseph Silk assumed a central black hole to very slowly grow from zero to one million solar masses, such that the gravitational potential would only change ever so slightly during a single orbit of a dark matter particle. This is called adiabatic growth. Particles keep a set of constants of motion fixed, such that their orbits shrink as the black hole grows and particles that originally lived at large distances end up at much smaller ones. The resulting dark matter density profile is a so-called spike (see figure 2), which is an extreme density enhancement within the sphere of gravitational influence of the final central black hole.
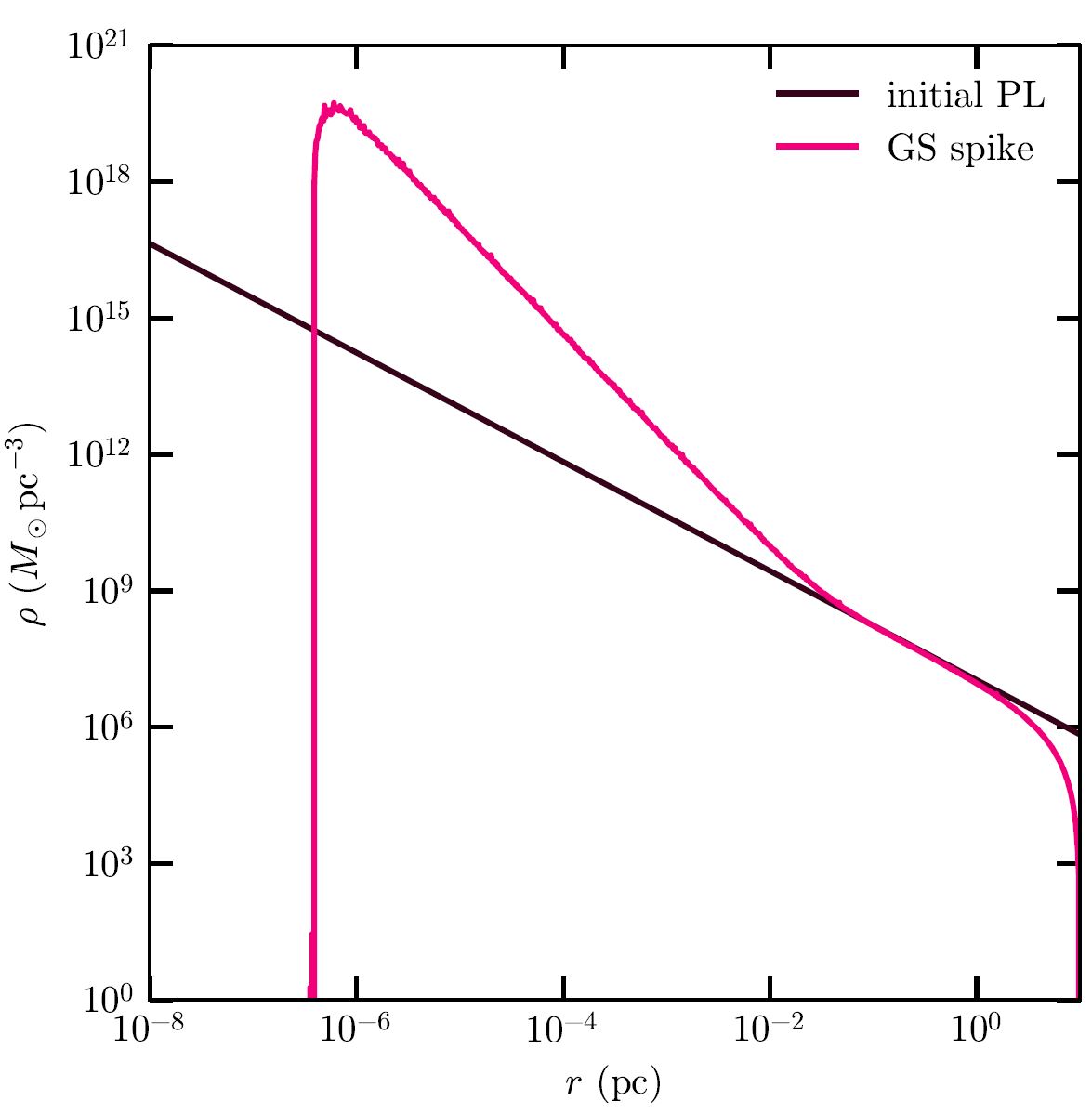
These spikes are the current basis for research into the detectability of dynamical friction effects in EMRIs. Many efforts are currently being made into computing accurate waveforms for such inspirals, as those are a key necessity for a successful gravitational-wave analysis. However, the existence of a spike is the result from a simpler toy model. This was sufficient for the study by Gondolo and Silk, as the self-annihilation of WIMPs would flatten the spike in the central regions, and deviations from the adiabatic growth toy model would disappear. On the other hand, if dark matter does not self-annihilate, then those details would be preserved, and the effect of dynamical friction would change in the inner regions. We thus want to study the shape of the dark matter halo in the central regions around a black hole that was ‘grown’ in the computer under realistic circumstances, and compare the impact of dynamical friction in realistic halos to the impact of the currently-used spikes from the adiabatic toy model.
Realistic systems do not tend to be exactly solvable, so instead we aim to build a toolbox that can numerically solve the equations for the evolution of a halo under the formation and growth of a central object. This object can be a black hole, but also a star or even a gas cloud, greatly extending the kinds of systems we can study. In my thesis, I present our numerical implementation for adiabatic growth, and verify that it indeed produces the same results as the analytical predictions from Gondolo & Silk. The inclusion of the capture of particles, a general relativistic effect, is a bit dodgy given the fact that this is a Newtonian formalism where general relativity is not included. However, we do include the prescription from Gondolo and Silk, since capture modifies the density in the central region around a black hole, which is our region of interest.
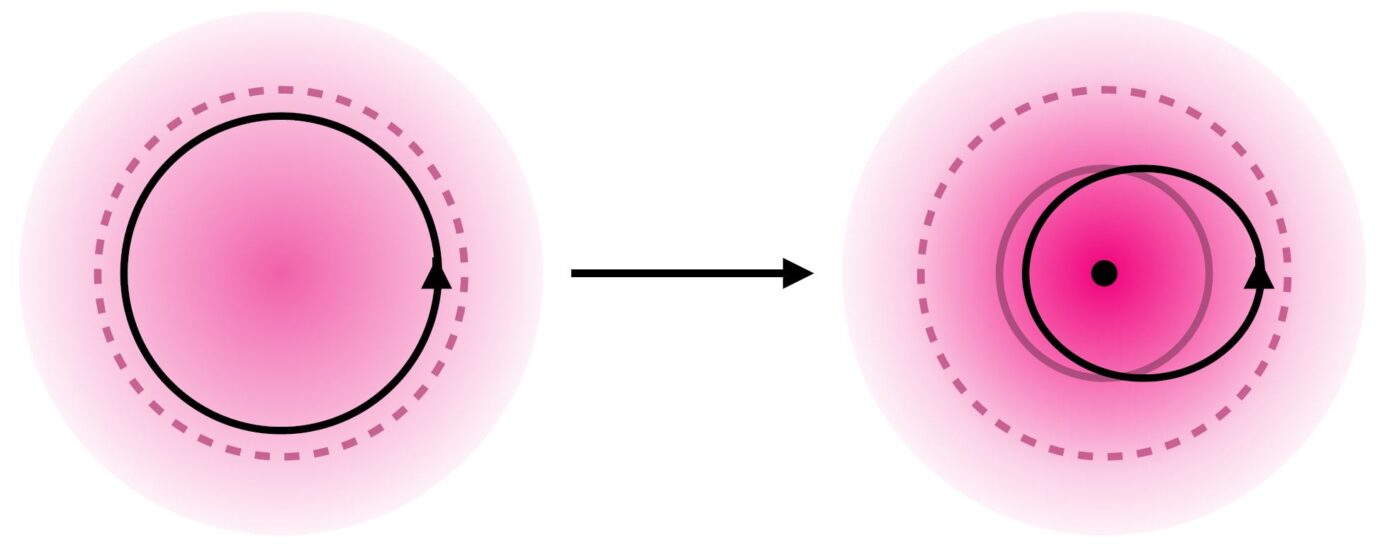
Not all processes are adiabatic however, and we would like a toolbox that can deal with as many different processes as possible. We thus turn our attention to the opposite end of the spectrum, with processes that happen approximately instantaneously, meaning that the change in the potential happens on timescales that are much smaller than that of a particle’s orbit. This fundamentally changes how the orbit adjusts to the new potential, where instead of a gradual contraction we now see an extreme shift of the pericentre (the point of the orbit closest to the black hole) towards the centre of mass see figure 3. This in turn changes the slope of the spike compared to the adiabatic case (see figure 4), because particles spend the majority of their time around their apocentres (the point of the orbit furthest from the black hole), so shifts in the pericentre have a much smaller impact on the overall density.
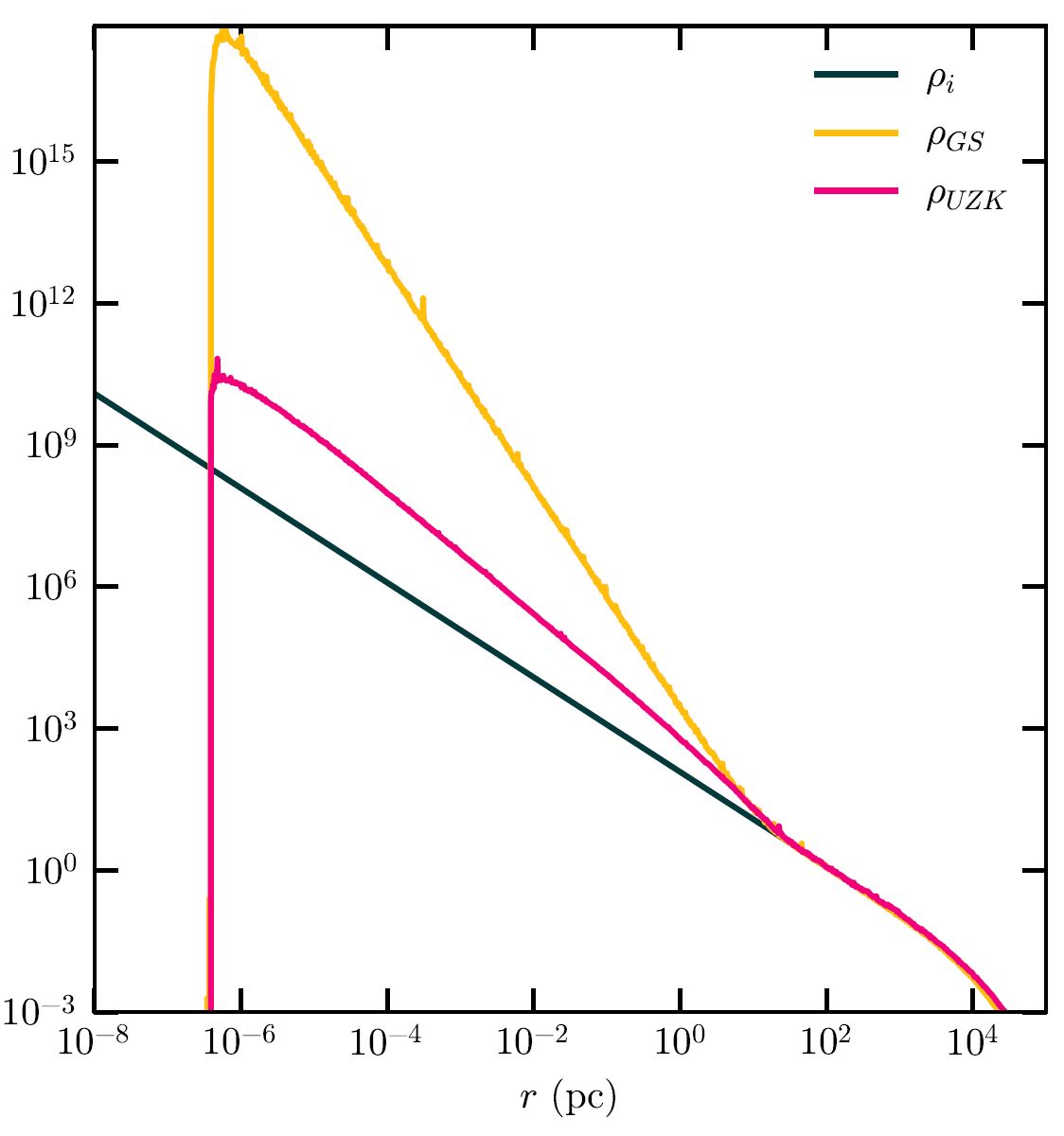
The original instantaneous formalism was devised by Piero Ullio, HongSheng Zhao and Marc Kamionkowski as part of a set of caveats to the calculations from Gondolo and Silk. They assumed exclusively initially circular orbits, so in the research described in my thesis we first extend their formalism to all possible initial orbits, and then present our numerical implementation. We again verify that our numerics give the same results as the analytical predictions from Ullio, Zhao and Kamionkowsku, although the initially elliptical orbits do exhibit some non-trivial behaviour compared to the initially circular predictions. Once again, our numerical implementation can deal with any type of extended object, compared to just a black hole in the original calculation.
Our toolbox now consists of adiabatic and instantaneous processes. We will thus need to examine black hole formation through this lens, and quantify the accuracy of approximating baryonic processes as either one or the other. In my thesis, we review three different scenarios for black hole formation during the era of the first stars, which is a very active field of research. The scenario that seems the best suited for spike formation is the formation of a black hole from a supermassive star (SMS). Under a set of very extreme conditions, a gas cloud of 105 − 106 solar masses can collapse without fragmenting, forming a singular star of similar mass. More precisely, these supermassive stars are the result of a protostar accreting matter at extremely high rates for extended periods of time, where the infalling material is provided by the collapse of the cloud. When the star then reaches the end of its life, it collapses without exploding, and the large majority of the star’s mass ends up in the final black hole, which is sometimes called a direct-collapse black hole because it forms almost directly from the collapse of the cloud.
The spherically symmetric nature of black hole formation through an SMS and the large final masses make it an ideal case study of realistic black hole formation with our new toolbox. We work through this in my thesis, where we approximate the formation of the SMS as adiabatic and the collapse of the star to be instantaneous. We find that the extended nature of the SMS has a dramatic impact on the final dark matter density – see figure 5. Inside the stellar core, the density is roughly constant and the gravitational potential flattens instead of following the shape of the black-hole potential. This significantly flattens the final density within that region after SMS formation, and the collapse of the star cannot sufficiently grow the spike to make up for it. Since the density is lowered inside of the former stellar core, or in other words, the spike has its edge taken off because of the inclusion of baryonic processes, we coin the term blunt dark matter spikes for these density profiles.
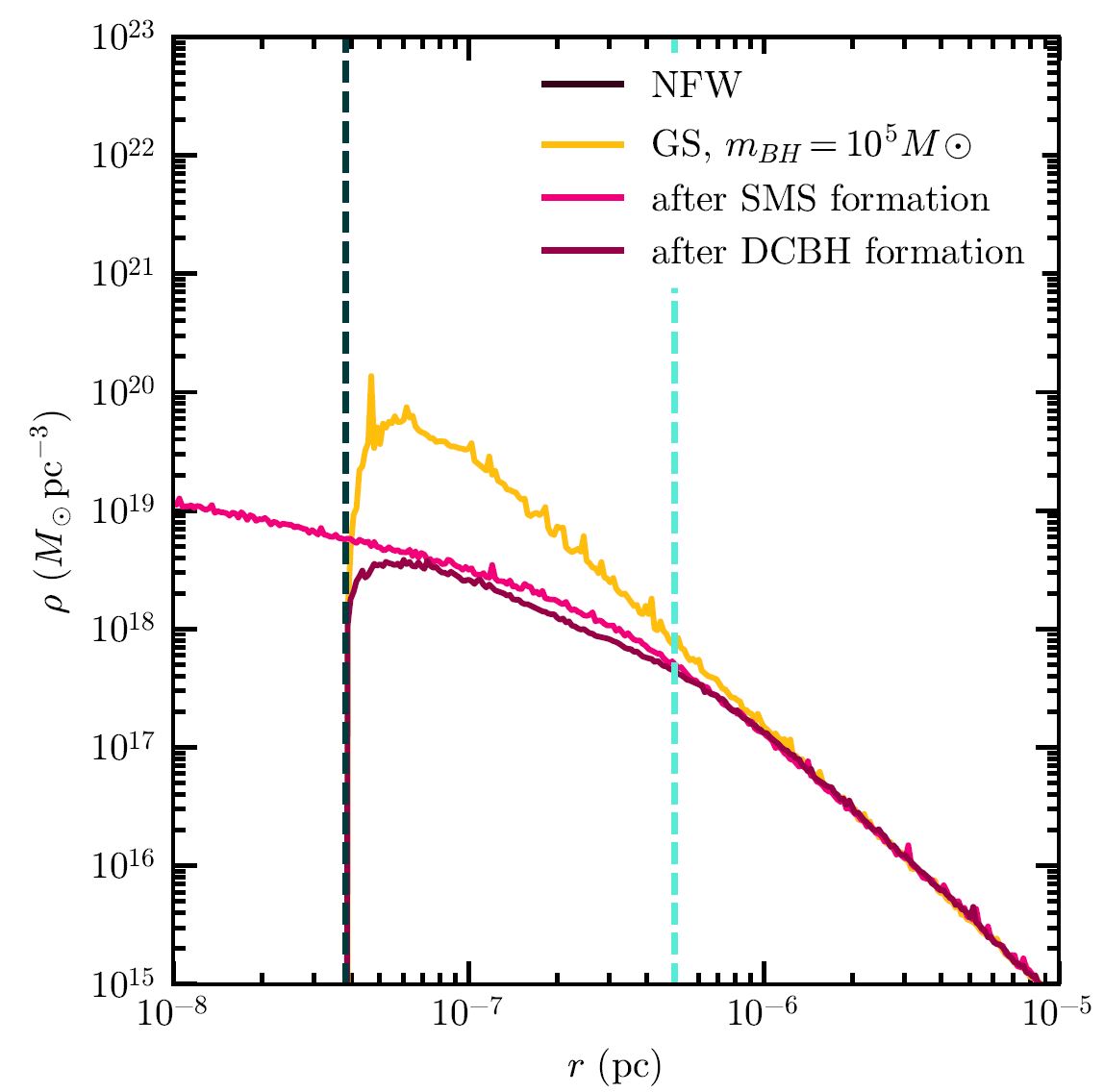
Blunt dark matter spikes have the potential to seriously impact detection prospects of dark matter imprints on EMRIs. The future space-based LISA detector will be able to detect EMRIs, and its planned observing time will be five years. For the reference system used in my thesis, the inspiral takes about 1.65 million cycles to inspiral in five years. If the inspiral is embedded in a spike based on GS predictions, an inspiral that takes five years does so in 690 cycles less than in vacuum. In our blunt spike, the density is lowered by roughly a factor 10 inside the inspiral region compared to the GS spike. Since dephasing is the cumulative effect of dynamical friction, the change in number of cycles is lowered more than the density. We find that the difference in number of cycles between a vacuum inspiral and a blunt spike inspiral is only 12 cycles, over a factor 50 less than for a GS spike.
This impacts both detectability and distinguishability. In principle, a dephasing of only a few radians is already detectable, so a change of 12 cycles should be detected just fine. However, if the inspiral is not detected for the full observing time, then the change in number of cycles could become too small and would go unnoticed. Furthermore, dark matter is not the only black hole environment that can impart a dephasing. Most notably, accretion disks – disks of infalling matter around heavy objects – alter the inspiral as well but with a somewhat different signature, and it remains an open question whether 12 cycles is enough to distinguish whether the dephasing came from a dark matter halo or an accretion disk.
Now, we performed these calculations based on a singular black hole formation setup and a singular EMRI system. Along with investigating detectability, predictions for blunt spikes should be made more robust by considering a wider variety of supermassive stars, different formation channels, as well as the impact of additional black hole growth. These processes should then also be placed within a cosmological context to quantify the probability of dark matter embedded EMRIs actually forming. Hopefully, the toolbox that we have developed will be useful in these future studies. Accurately describing embedded EMRIs is an important endeavour, as a positive detection would be the first time dark matter is probed on such small scales. This could thus provide novel clues about the true nature of dark matter, which is why we have been devoting our time and effort to this topic.
Time is luckily not of the essence at the moment, as LISA’s planned launch is currently in the year 2037. By preparing an as exhaustive as possible set of analyses before it launches, we can maximise the science return once it’s up in space and working away. Though I will be honest, a bit of procrastination has never hurt anyone, and my bed is looking very comfy right about now, so the science will have to wait a little bit. Good night, sleep tight, and sweet dreams.