
’t Hooft wordt op zijn 78-jarige leeftijd nog steeds beschouwd als een van de succesvolste theoretische natuurkundigen ter wereld. Acht jaar geleden is er op deze website al een artikel verschenen over de belangrijkste prestaties van ’t Hooft, maar laten we er nog eens snel op terugblikken. Het bekendst is de Nederlander door zijn werk aan dimensionele regularisatie en renormalisatie, technieken die ervoor zorgen dat uitkomsten van berekeningen in quantumveldentheorie eindig zijn in plaats van oneindig. Dit zorgde ervoor dat de theorie bruikbaar werd en kon worden gebruikt voor nauwkeurige voorspellingen, die vervolgens getest konden worden met bijvoorbeeld de deeltjesversneller van CERN. Dit werk heeft ’t Hooft zowel de Nobelprijs van 1999 (gedeeld met de Nederlander Martinus Veltman, zijn promotor ten tijde van het onderzoek) als de prijs van afgelopen april opgeleverd.
Daarnaast heeft ’t Hooft ook ander werk gedaan aan de quantumchromodynamica, de theorie die quarks en de sterke kernkracht in het standaardmodel beschrijft. In deze theorie is het moeilijk om berekeningen te doen; om dit op te lossen bedacht ’t Hooft dat het makkelijker was om het aantal ‘kleuren’ (normaal zijn dat er drie) heel groot te nemen en resultaten daarvandaan te extrapoleren terug naar drie kleuren. Een bijkomstigheid was dat de uitkomsten van de berekeningen later erg bleken te lijken op uitkomsten in snaartheorie, wat leidde tot de AdS/CFT-correspondentie. Dit laatste wordt vaak in één adem genoemd met een ander idee van ’t Hooft: het holografisch principe, ontwikkeld door hem en de Amerikaan Leonard Susskind. Dit principe zegt dat de maximale hoeveelheid informatie die een bepaald volume in de ruimte kan bevatten evenredig is met de oppervlakte van dit volume, en wordt vaak geïnterpreteerd als het feit dat alle informatie af te lezen zou zijn aan de buitenkant van dit volume.
De invloeden van ’t Hooft op de natuurkunde en de rest van de academische wereld zijn niet alleen te merken in zijn eigen werk, maar ook in het grote aantal bekende mensen die hij heeft opgeleid. Zo zijn bijvoorbeeld Robbert Dijkgraaf (hoogleraar aan de Universiteit van Amsterdam en voormalig minister van Onderwijs, Cultuur en Wetenschap), Herman Verlinde (hoogleraar in de natuurkunde aan het IAS Princeton) en Max Welling (hoogleraar machine learning aan de Universiteit van Amsterdam) gepromoveerd bij ’t Hooft. Op deze manier stam ik zelf ook af van ’t Hooft; mijn begeleider Hessel Posthuma is namelijk gepromoveerd bij Robbert Dijkgraaf!
Voor regelmatige lezers van de Quantum Universe-website moge het duidelijk zijn: de ideeën van ’t Hooft worden vaak genoemd in de artikelen op deze website, want ze hebben een grote invloed gehad op de theoretische natuurkunde en worden op grote schaal gebruikt. Dit komt door de intelligentie van ’t Hooft, maar ook doordat hij tegen de stroom in durft te gaan en op zijn eigen manier denkt. Zo schreef Susskind1; dat een typisch gesprek tussen hem en ’t Hooft als volgt ging (vrij vertaald):
LS: “Gerard, ik ben het volledig met je eens!”
GtH: “Dat kan wel, maar ik ben het volledig oneens met jou.”
Zo denkt ’t Hooft ook anders over de quantummechanica dan de meeste natuurkundigen; hij zegt dat die theorie deterministisch is. Maar wat houdt dat precies in?
Determinisme en quantummechanica
Het doel van de natuurkunde is het beschrijven van processen die plaatsvinden in ons universum, zowel op de allergrootste als de allerkleinste schaal. Met de wetten van Newton bleek hier een leuke bijkomstigheid: de wiskundige beschrijving maakte het mogelijk om de toekomst heel precies te voorspellen. Die wetten van Newton geven namelijk aan hoe de beweging van objecten met massa verandert zodra er een kracht op werkt. Een veelgebruikt voorbeeld: stel je een bal voor op een helling, en stel je voor dat je precies weet wat de hoek van de helling is en hoe groot en zwaar de bal is. Dan kun je, met behulp van de valversnelling en de wetten van Newton, precies uitrekenen hoe de bal gaat rollen en daarmee waar de bal op een later moment in de tijd zal zijn. Oftewel, gegeven de precieze beginvoorwaardes weet je met zekerheid de eindtoestand; dat laatste bedoelen we als we zeggen dat het proces deterministisch is.
Ook de later ontwikkelde elektrodynamica van o.a. Maxwell en de algemene relativiteitstheorie van Einstein zijn deterministisch. Gegeven de precieze begintoestand kan, met behulp van de wiskundige beschrijving van de theorieën (en genoeg rekenkracht), de precieze eindtoestand worden uitgerekend. Ook de statistische fysica is in principe deterministisch, maar in de statistische fysica wordt erkend dat er in bepaalde gevallen niet genoeg rekenkracht is om écht alles vanuit een specifieke begintoestand te beschrijven, dus wordt statistiek gebruikt om achter het collectieve gedrag van een grote hoeveelheid deeltjes te komen.
De hierboven genoemde theorieën bij elkaar vormen echter niet een complete beschrijving van de natuur. Er zijn verschijnselen die niet verklaard kunnen worden aan de hand van bovengenoemde (deterministische) theorieën. Voorbeelden van deze verschijnselen zijn zwarte stralers en het foto-elektrisch effect, die recent al in dit artikel zijn genoemd en in meer detail zullen worden beschreven in toekomstige artikelen in de quantumpioniers-reeks. De succesvolste theorie die wél in staat is veel van deze verschijnselen te beschrijven, is quantummechanica. Maar in de huidige wiskundige beschrijving van de quantummechanica is determinisme niet aanwezig. Alhoewel, je kunt beargumenteren dat dit afhangt van de precieze interpretatie die wordt gebruikt. Dit is een filosofische kwestie waar ik nu niet heel uitgebreid op in zal gaan. Er is al wat over te lezen in dit artikel en wellicht kom ik hier ook op terug in de quantumpioniers-reeks.
Maar wat is er dan precies niet-deterministisch aan de quantummechanica? Kort gezegd volgt er uit de rekenregels dat, gegeven een begintoestand, niet precies kan worden voorspeld wat de eindtoestand is. Er kan slechts een kans worden bepaald dat een systeem in een mogelijke eindtoestand terechtkomt. Ik zal dit illustreren aan de hand van het bekende voorbeeld van Schrödingers kat.
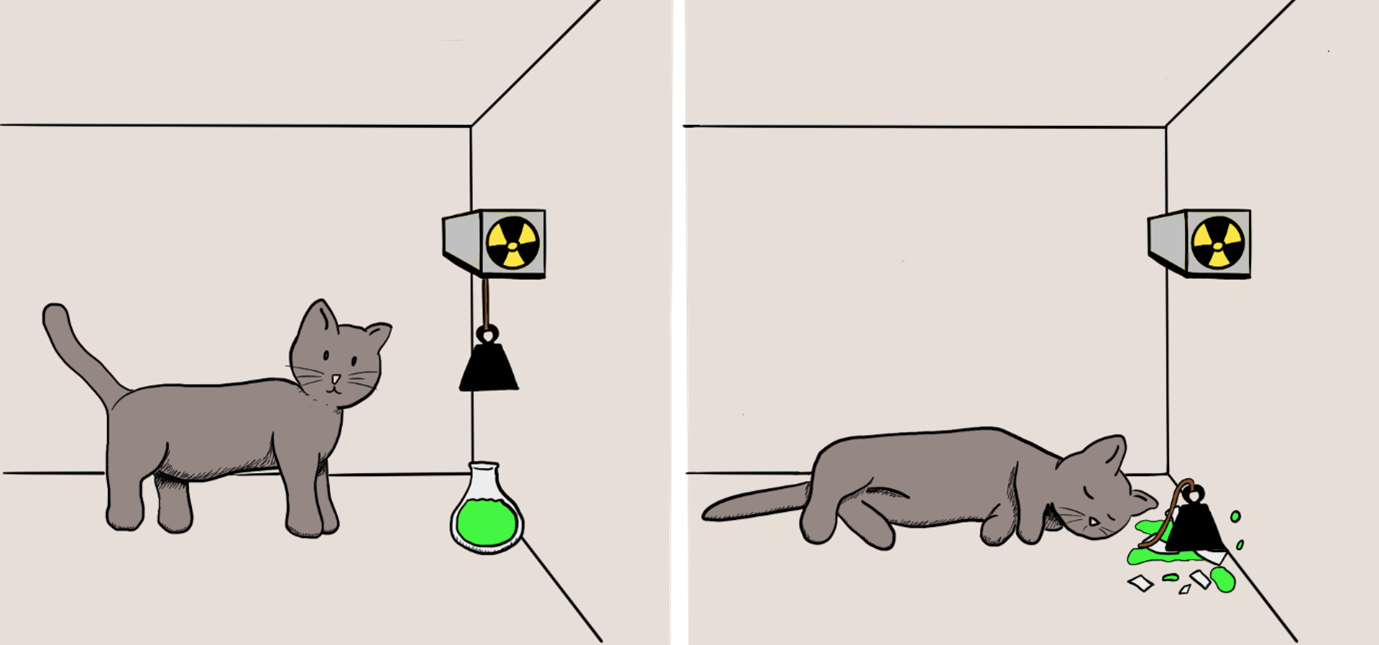
Men neme (hypothetisch) een levende kat en een flesje met gif bevestigd aan een systeem dat ervoor zorgt dat het flesje stuk gaat zodra er een atoom vervalt. Vervolgens legge men zowel de kat als dit flesje gif in een afgesloten doos. Zo wordt het lot van de kat gekoppeld aan het wel of niet vervallen van het atoom. Als het atoom vervalt, breekt het flesje gif en komt de kat te overlijden, maar zolang het atoom niet vervalt blijft het flesje heel en blijft de kat leven. Het punt is nu dat we niet weten wanneer het atoom komt te vervallen, dus zodra er wat tijd is verstreken kunnen we niet met zekerheid zeggen of de kat dood of levend is. Wat de quantummechanica zegt (of om precies te zijn: wat de Kopenhagen-interpretatie van de quantummechanica zegt) is dat de kat tegelijkertijd dood én levend is, en zich bevindt in een zogenaamde superpositie van toestanden, waarin het dier is verstrengeld met het atoom. Pas als we de doos openmaken zien we of de kat dood of levend is. Dat wil zeggen: zodra we de doos openmaken ‘stort de toestand van de kat in’ naar één van de twee mogelijkheden.
Paradoxen
Verstrengelen van toestanden en de instorting bij een meting leiden tot verscheidene problemen. De vraag wat er gebeurt bij het openmaken van de doos, en of de toestand daarbij instort, heet ook wel het meetprobleem. Je kunt daarover meer lezen in dit artikel. Verstrengeling van toestanden leidt tot de EPR-paradox, vernoemd naar de fysici Einstein, Podolski en Rosen, die de paradox formuleerden in een artikel van 90 jaar geleden, uit mei 1935. Kort gezegd luidt de paradox als volgt: stel je voor dat we niet de toestanden van de kat en het atoom verstrengelen, maar in plaats daarvan de toestanden van twee fotonen, oftewel twee lichtdeeltjes. Wat bijvoorbeeld in een verstrengelde toestand gebracht kan worden, is de polarisatie van de twee lichtdeeltjes naar óf allebei verticaal óf allebei horizontaal. Zodra we dan van één foton de polarisatie meten, bepalen we ook de polarisatie van het andere foton, doordat de toestand instort naar die waarin beide fotonen de gemeten polarisatie hebben. Maar stel nu dat we één van de twee fotonen naar een plek ver weg sturen. Dan ligt de polarisatie van het foton dat ver weg is vast zodra we de polarisatie van het andere foton meten. Op die manier lijkt het alsof we onmiddellijk informatie van onze plek waar we meten naar de plek ver weg hebben gestuurd, maar tegelijkertijd kan volgens de relativiteitstheorie niets zich sneller verplaatsen dan de lichtsnelheid. Een paradox!
De paradox zelf is eenvoudig opgelost: bij nader bestuderen ontdek je namelijk dat er op deze manier toch geen signalen met meer dan de lichtsnelheid kunt versturen. Dat komt doordat je vooraf niet kan bepalen wat de polarisatie van het ver verwijderde foton gaat worden. Dat neemt niet weg dat het heel tegenintuïtief voelt dat je zonder tijdsverschil iets op grote afstand kunt beïnvloeden. Er bestaat een wiskundige ongelijkheid die nauw samenhangt met dit tegenintuïtieve verschijnsel. Of aan die ongelijkheid voldaan is, kan bovendien gemeten worden in een lab. De uitkomst van een zeker experiment zou, als de principes van de quantummechanica kloppen, uitkomen boven een bepaalde waarde, terwijl de uitkomst juist onder die waarde uitkomt als de principes niet kloppen. De ongelijkheid waar ik het over heb wordt de ongelijkheid van Bell genoemd, en of er wel of niet aan de ongelijkheid voldaan is, is met zeer hoge precisie gemeten in een experiment in Delft, ten voordele van de quantummechanica. Betekent dat dan dat het kans-aspect van de quantummechanica een fundamentele eigenschap ervan is, en dat ons universum dus niet deterministisch is?
Integendeel, volgens ’t Hooft
Hoewel de experimenten lijken te bevestigen dat de ongelijkheid van Bell de quantummechanica gelijk geeft, is ’t Hooft niet overtuigd. Volgens hem moeten de wetten van het universum lokaal zijn (dus niet afhangen van wat er ver weg gebeurt) en deterministisch, wat nu juist door de ongelijkheid van Bell uitgesloten lijkt te worden. Maar de ongelijkheid van Bell is gebaseerd op een aantal aannames, waarvan de bekendste het al dan niet bestaan van zogenaamde ‘verborgen lokale variabelen’ is. Het zijn de overige aannames die volgens ’t Hooft onjuist zijn2.
De aanname waar het over gaat is, kort gezegd, het bestaan van ‘vrije wil’. Voor de ongelijkheid moeten twee hypothetische waarnemers worden geïntroduceerd, die vaak Alice en Bob genoemd worden. Alice en Bob moeten kiezen wat ze meten, op basis van vrije wil. Maar als de werkelijkheid deterministisch is en alle processen met oneindige precisie kunnen worden voorspeld, bestaat vrije wil niet. Wat Alice en Bob kiezen is dan dus niet vrij, maar ligt al van tevoren vast, zelfs al vanaf het ontstaan van het universum. Hiermee zijn de ideeën van ’t Hooft niet in strijd met de uitkomt van het experiment in Delft.
Toch is het niet zo dat ’t Hooft zegt dat de quantummechanica onjuist is: volgens hem zijn alleen de conclusies die eruit worden getrokken onjuist. Denk terug aan de kat van Schrödinger, die zich op het moment van schrijven nog steeds in de doos bevindt. We concludeerden dat de kat dood én levend tegelijk is, totdat we de doos openmaken. Maar volgens ’t Hooft is dit niet écht wat de realiteit is; we nemen de uitkomst té letterlijk. In werkelijkheid zou de kat zich in één van de twee toestanden bevinden, maar we weten niet met zekerheid welke omdat we niet genoeg informatie over de begintoestand hadden. De superpositie reflecteert slechts de kans waarmee de kat zich in een van de twee posities bevindt. Met andere woorden (die van ’t Hooft)[3]: de onzekerheid in de eindtoestand reflecteert slechts de onzekerheid in de begintoestand.
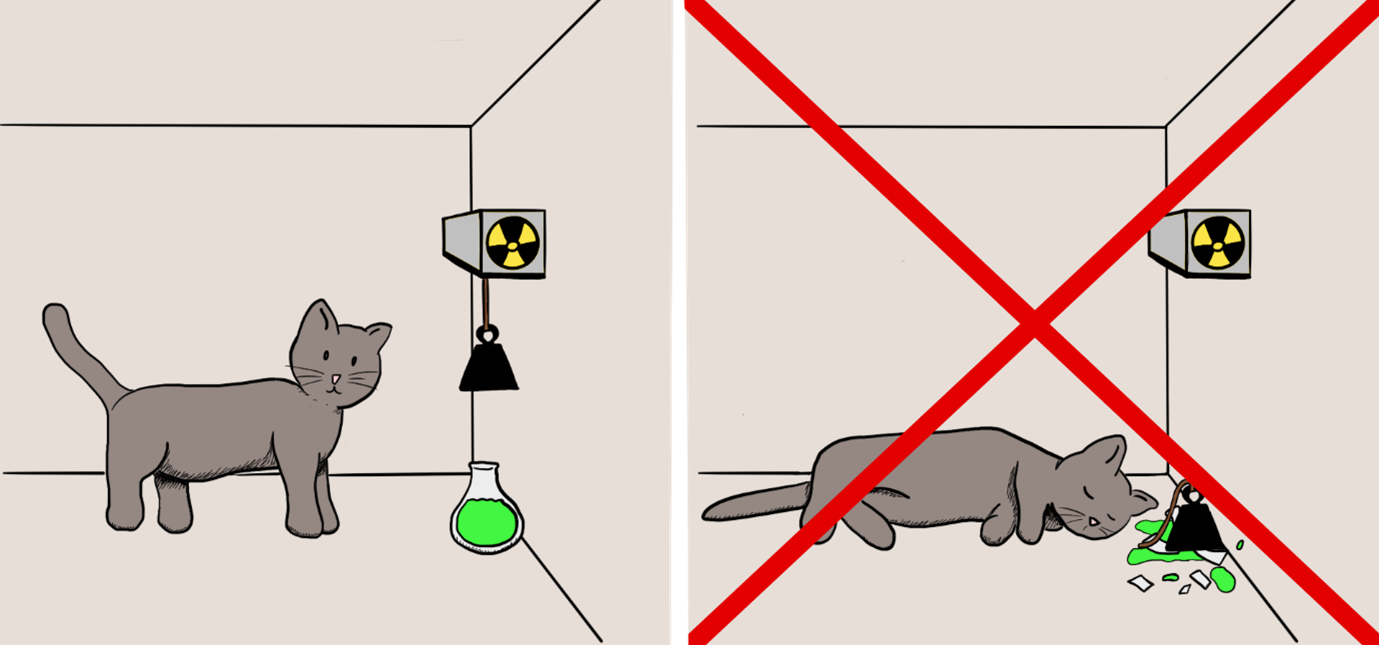
De wiskundige beschrijving van de quantummechanica is dus juist, maar alsnog niet deterministisch. Om de interpretatie van ’t Hooft hard te maken, is er dus een nieuwe onderliggende wiskundige beschrijving nodig, die deterministisch is maar tegelijkertijd de quantummechanica niet tegenspreekt. Dat weet ’t Hooft natuurlijk ook, dus om zijn woorden kracht bij te zetten heeft hij ze van een wiskundige beschrijving voorzien. De details gaan te ver om in dit artikel op in te gaan, maar voor de ingelezen lezer is de beschrijving – en nog veel meer – te vinden in het boek dat ’t Hooft over zijn interpretatie heeft geschreven: ‘The Cellular Automaton Interpretation of Quantum Mechanics’.
Er zijn op dit moment nog niet veel natuurkundigen die de interpretatie van ’t Hooft hebben omarmd, wat wellicht komt door het ongekende succes van quantummechanica in haar huidige vorm, die tot nu toe uitstekend werkt. Voordat een nieuwe theorie überhaupt in overweging genomen kan worden, moet deze uitvoerig bekeken worden. Desondanks denk ik dat een deterministische beschrijving van het universum wel fraai zou zijn, hoewel andere natuurkundigen daar misschien anders over denken. Verder moge het benadrukt worden dat ’t Hooft niet beweert dat de quantummechanica zelf fout is, maar hoe zij geïnterpreteerd wordt wel. Bij elkaar genomen geeft dit voldoende reden om de ideeën toch kritisch in overweging te nemen, zeker aangezien ze van zo’n creatieve natuurkundige als Gerard ’t Hooft komen!
[1] Dit schreef Susskind in zijn boek genaamd ‘The Black Hole War’, waar ik in de toekomst een recensie over hoop te schrijven voor op deze website.
[2] De argumenten van ’t Hooft zijn opgeschreven in zijn boek ‘The Cellular Automaton Interpretation of Quantum Mechanics’, waarop dit artikel ook is gebaseerd.
[3] Bron: epiloog van een wetenschappelijk artikel van ’t Hooft, geplaatst op Arxiv.
QU is sinds kort weer actief op Instagram! Volg ons voor nieuws en aankondigingen van nieuwe artikelen: https://www.instagram.com/quantumuniverse.nl/