Een quantumpomp
Zoals altijd is het de moeite waard om te beginnen met wat geschiedenis en achtergrondinformatie, voordat we naar het hoofdonderwerp van het artikel gaan. Zo is het goed om eerst te weten wat we bedoelen als we het hebben over een pomp. In dit artikel bedoel ik met een pomp een systeem dat, in de loop van de tijd, een bepaalde substantie transporteert. Dat kan transport zijn tussen verschillende locaties, zoals een normale waterput waarin water omhoog gepompt wordt van heel laag naar hoog, of misschien een apparaat dat iets ‘rondpompt’, zoals de cv-ketel water door de verwarmingsbuizen drukt. Een belangrijk detail is dat het uiteindelijk gaat om beweging of transport. Een pomp is dus een mechanisme dat iets laat bewegen. De pomp die in dit artikel van groot belang is, is de schroef van Archimedes, die je kunt zien in de afbeelding hieronder:
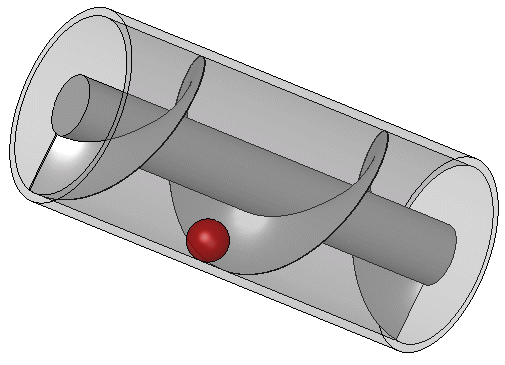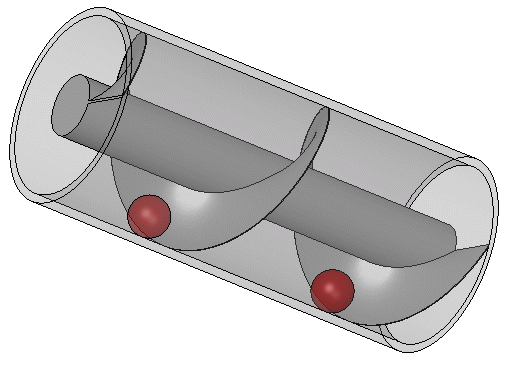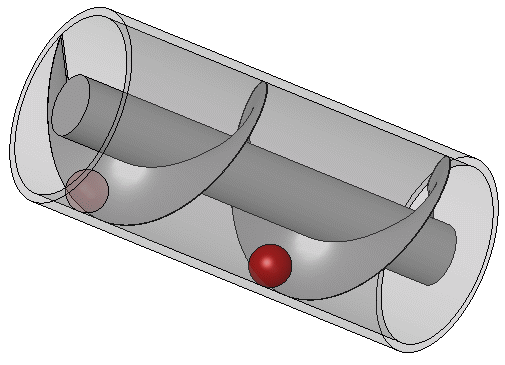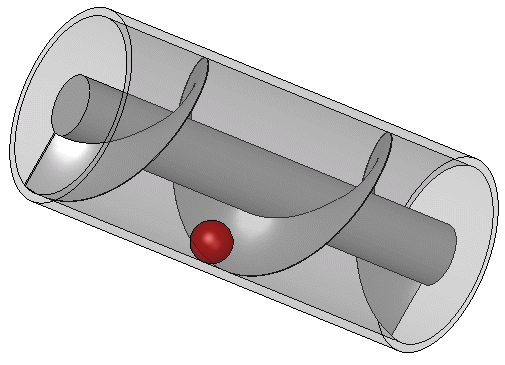
De schroef van Archimedes is een eenvoudig voorbeeld van een pomp. Zoals ik al zei, bestaat er van dit fenomeen ook een quantumvariant, die de Thouless-pomp genoemd wordt.
In zijn oorspronkelijke artikel uit 19831 beschouwde de natuurkundige David Thouless het concept van zogeheten adiabatisch transport (transport waarbij geen warmte met de omgeving wordt uitgewisseld) met een tijdsafhankelijke, periodieke potentiële energie. Met dat laatste bedoelde Thouless dat de potentiële energie van het systeem zich zowel in tijd als ruimte herhaalt – net als bij de schroef van Archimedes. Die schroef is namelijk een pomp die zowel in de loop van de tijd (na elke rotatie) als in de ruimte (elke ‘golflengte’ in de spiraal van de schroef) periodiek is. Wiskundiger beschreven: Thouless vond een oplossing voor de Schrödingervergelijking met een potentiële energie die er als volgt uit ziet2:
\( V(x,y,z,t) = V_0 (x,y,z) + V_1(x-vt,y,z) \).
Door de Schrödingervergelijking formeel op te lossen (en dus niet te kijken naar de specifieke vorm van de potentiële energie, maar puur naar de algebraïsche eigenschappen ervan) kon Thouless een formule afleiden die aangeeft hoeveel transport er plaatsvindt in dit systeem. Hiervoor maakte hij nog een specifieke aanname die ik hierboven al noemde: dat het transport ‘adiabatisch’ moest zijn. Dat wil in het bijzonder zeggen dat de snelheid \( v \) in de formule hierboven heel klein moet zijn ten opzichte van de zogenoemde relaxatietijd van het systeem: de tijdschaal waarop het systeem ‘uit zichzelf’ significant zou veranderen. Als de potentiële energie heel snel zou variëren, dan zou de oplossing van de Schrödingervergelijking (dus: de golffunctie) onnoemelijk veel complexer zijn. Een daadwerkelijk experiment is vrijwel altijd adiabatisch te maken, dus het adiabatisch zijn is ook een zeer redelijke fysische aanname. Een eenvoudig voorbeeld van een ’potentiële-energielandschap’ dat voldoet aan de formule hierboven:
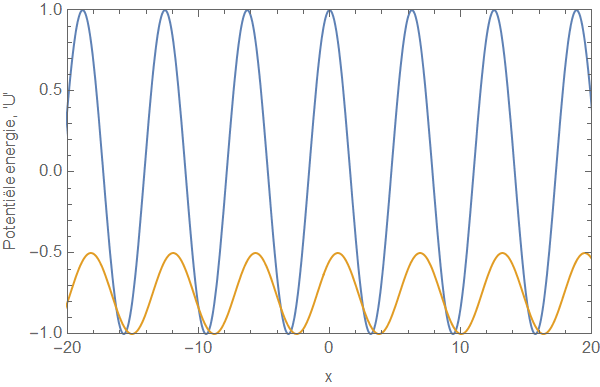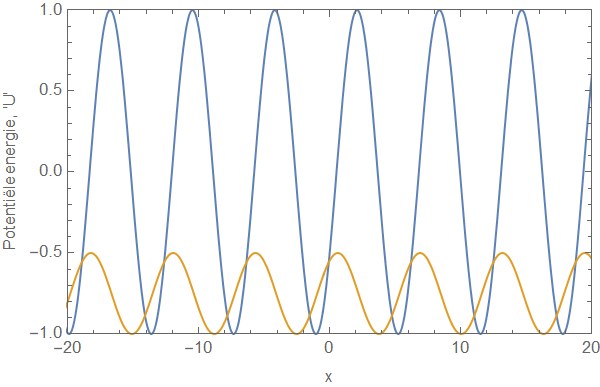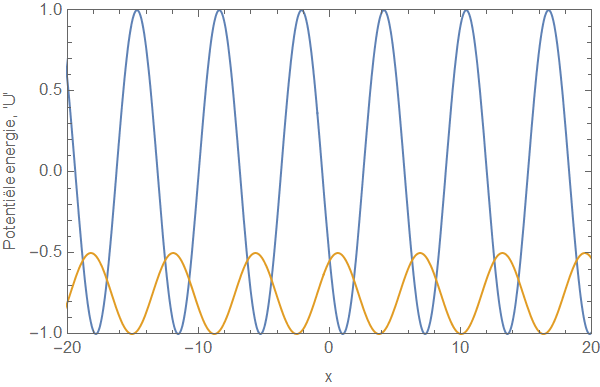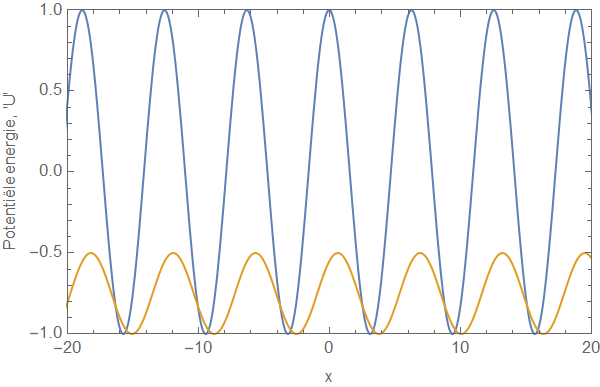
Thouless vond dus een algemene formule voor transport met een tijdsafhankelijke potentiële energie zoals die hierboven. We noemen de ‘waarde’ van dit transport in dit artikel C. Deze ‘C’ is zoiets als de ‘hoeveelheid deeltjes die in een bepaalde tijd worden rondgepompt’. Thouless begon met het bestuderen van een heel simpel geval, waarbij de potentiële energie gegeven is door één enkel ‘dal’ dat van links naar rechts beweegt. De golffunctie kan in dit geval expliciet uitgerekend worden, en er kan een waarde gevonden worden voor de hoeveelheid transport. Wat blijkt: C kan elke (continue) waarde aannemen, afhankelijk van de ‘diepte’ van de put.
Daarna bekeek hij een interessantere situatie. Thouless bekeek een systeem dat meer op een metaalrooster lijkt, waarbij er een zogenaamde bandenstructuur in de mogelijke energiewaarden van het systeem is. In dit geval bleek de waarde van C, gemeten in de juiste eenheden, alleen maar een geheel getal te kunnen zijn! Oftewel: de hoeveelheid rondgepompte substantie is ‘gequantiseerd’! Je kunt dit systeem dus met recht een quantumpomp noemen. Het getal C kon wiskundig worden geïdentificeerd als het zogenaamde Cherngetal: een getal dat in de topologie de meetkundige eigenschappen van een quantumsysteem karakteriseert.
Laat ik de laatste alinea illustreren aan de hand van een voorbeeld en gedachte-experiment.
Een voorbeeld en gedachte-experiment
De rest van dit artikel is deels gebaseerd op tekst die je kunt vinden op de website topocondmat.org van de TU Delft. Op deze website worden veel concepten van topologische quantummaterialen behandeld. Ik vond de argumentatie op de website erg verhelderend, en wil iets vergelijkbaars hier delen.
Als potentiële energie nemen we de situatie die is weergegeven in afbeelding 2. Hieronder, in afbeelding 3, is een momentopname weergegeven. De potentiële energie die we zien lijkt op die van een metaalrooster: een (in de ruimte) periodieke potentiaal. In zulke potentialen blijkt, zoals ik al kort aanstipte, dat de energie van de bijbehorende golffunctie een bandstructuur heeft. De bandstructuur geeft de relatie weer tussen de energie van de golffunctie, en de bijbehorende impuls, een maat voor de hoeveelheid beweging. De bandstructuur voor de potentiaal hieronder ziet eruit zoals in de afbeelding rechts. Elke lijn komt overeen met een bepaalde (aangeslagen) toestand van de golffunctie. Deze golffunctie beschrijft op zijn beurt weer het hele quantumsysteem, bijvoorbeeld een verzameling elektronen. Wat opvalt, is dat de onderste twee lijnen voor elke waarde van de impuls k gescheiden zijn van andere lijnen. Dat komt doordat deze quantumtoestanden gebonden toestanden zijn, waarbij het systeem zich bevindt onderin de ‘dalen’ van de potentiële energie. De deeltjes of andere componenten van het systeem zijn daar dus gebonden: opgesloten. Dit alles betekent dat er geen overlap is van deze toestanden met toestanden in andere dalen, en dát betekent weer dat er geen mogelijkheid is voor zo’n toestand om te ‘springen’ tussen de dalen. De energie kan daarom niet afhangen van beweging, en is daarom vrijwel constant, hetzelfde voor elke impuls.
Met het bovenstaande in gedachten is het niet moeilijk om te beredeneren dat tijdens elke periode van de potentiaal, alle N deeltjes die zich diep in de potentiële-energieput bevinden ook allemaal verplaatst worden. Deze toestanden bewegen immers netjes mee met de dalen van de potentiaal, vergelijkbaar met wat er gebeurt in een schroef van Archimedes. N is een geheel getal – met andere woorden: het transport is gequantiseerd!
Zo zien we dat een idee dat Archimedes al tweeduizend jaar geleden bedacht, door Thouless in een quantumjasje gegoten kon worden. Het is een mooi voorbeeld van hoe bijna alles in de ‘klassieke’ natuurkunde wel een intrigerende quantumtegenhanger heeft.
[1] Het oorspronkelijke artikel van Thouless is niet als open-accesspublicatie verkrijgbaar. Dat is jammer, aangezien het een prachtige berekening betreft voor het vinden van, en analyseren van golffuncties. In dit artikel vat ik samen wat Thouless gedaan heeft, en beschrijf ik de resultaten die daardoor gevonden zijn.
[2] Technisch gezien moeten in deze vorm de potentialen \(V_0\) en \(V_1\) nog eenzelfde golflengte L hebben en moet de verhouding van L en v een geheel getal keer de periode T zijn. De potentiaal in afbeelding 2 voldoet aan deze eisen.