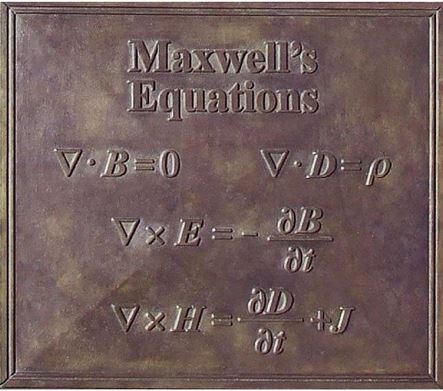
Dat deze fenomenen vandaag de dag zo gewoon zijn, is te danken aan een groot aantal natuurkundigen die hier in de 19e eeuw onderzoek naar deden, en in het bijzonder aan James Clerk Maxwell. De Schotse natuurkundige vatte de theorie van elektromagnetisme samen in elegante vergelijkingen, die nog steeds de basis vormen van ons begrip van elektriciteit en magnetisme.
Lange tijd werd gedacht dat elektriciteit en magnetisme twee onafhankelijke fenomenen zijn. Daar kwam verandering in toen de Deense natuurkundige Hans Christian Ørsted in 1820 ontdekte dat de naald van een kompas beweegt als deze zich in de buurt van een elektrische stroom bevindt. Ørsted toonde hiermee aan dat er wel degelijk een verband is tussen elektriciteit en magnetisme, en inspireerde veel van zijn natuurkundige tijdgenoten tot onderzoek om dit verband beter te begrijpen. Zo ontdekte André-Marie Ampère dat twee parallelle stroomdraden elkaar magnetisch aantrekken als de stromen in dezelfde richting lopen, en elkaar afstoten als de stromen in tegenovergestelde richting lopen. In 1825 maakte hij deze observatie wiskundig precies met een vergelijking – nu bekend als de krachtenwet van Ampère – die de aantrekkende of afstotende magnetische kracht tussen de twee stroomdraden beschrijft. Enkele jaren later, in 1831, publiceerde Michael Faraday zijn ontdekking van elektromagnetische inductie, het verschijnsel waarbij een veranderend magnetisch veld zorgt voor de opwekking van een elektrische stroom. Heinrich Lenz bouwde hierop voort en beredeneerde in 1834 wat de richting van de bijbehorende inductiestroom moest zijn.
Wie op dit punt de draad kwijtraakt, is zeker niet de enige. In de jaren na Ørsteds ontdekking volgden nieuwe theorieën en experimentele resultaten over elektriciteit en magnetisme elkaar in rap tempo op, maar een overzichtelijke beschrijving die al deze resultaten omvatte, bleef uit tot het werk van James Clerk Maxwell. Tussen 1856 en 1873 publiceerde Maxwell een aanzienlijk aantal wetenschappelijke artikelen over elektromagnetisme, de overkoepelende term voor elektriciteit én magnetisme. In het bijzonder vatte Maxwell in zijn artikel “A Dynamical Theory of the Electromagnetic Field” de theorie van het elektromagnetisme samen in een twintigtal wiskundige vergelijkingen. Hiermee legde hij de basis voor het hedendaagse begrip van elektromagnetische verschijnselen.
Dat ik in dit artikel geen twintig, maar slechts vier vergelijkingen hoef te bespreken, is te danken aan Oliver Heaviside. De Engelse wiskundige herschreef het werk van Maxwell naar het viertal vergelijkingen die vandaag de dag bekend staan als de wetten van Maxwell of de Maxwellvergelijkingen.
De taal van de Maxwellvergelijkingen
De Maxwellvergelijkingen geven een korte en bondige manier om een omvangrijke theorie op te schrijven, maar voor wie niet erg thuis is in de wiskunde, kan het viertal vergelijkingen er behoorlijk intimiderend uitzien. De vergelijkingen beschrijven elektriciteit en magnetisme in termen van elektrische en magnetische velden. In abstracte termen is een veld een functie die aan iedere positie in de ruimte op elk moment in de tijd bepaalde waardes toekent. Dit lijkt misschien ingewikkeld, maar kan in de praktijk erg handig zijn. Stel bijvoorbeeld dat je de temperatuur in een kamer op een bepaald moment wil beschrijven. De temperatuur zal niet overal hetzelfde zijn: dicht bij de verwarming is de temperatuur wat hoger, in de buurt van het raam wat lager. Om de temperatuur nauwkeurig te beschrijven, moet je deze voor iedere plek van de kamer apart noteren. Het resultaat is een functie die voor iedere locatie in de kamer de temperatuur op die locatie geeft. Als je dit ook nog eens op verschillende momenten doet, bijvoorbeeld om weer te geven wat er gebeurt als de verwarming hoger wordt gezet, krijg je een functie van ruimte én tijd. Deze functie zou je het ‘temperatuurveld’ kunnen noemen.
Een ander voorbeeld is de stroming van een vloeistof, zoals water. Om de stroming te beschrijven, wil je op iedere plek en op elk moment weten hoe snel en in welke richting het water stroomt. De waardes van het ‘waterstromingsveld’ zijn nu geen getallen, zoals bij de temperatuur, maar pijltjes die zowel een grootte als een richting hebben (in wiskundige termen: vectoren). Hoe groter de pijl op een bepaalde plek, hoe sneller het water daar stroomt.
Elektrische en magnetische velden zijn, net als het waterstromingsveld, voorbeelden van vectorvelden. Een elektrisch veld beschrijft de kracht die een geladen voorwerp uitoefent op andere geladen voorwerpen. Die andere geladen voorwerpen hoeven er niet daadwerkelijk te zijn: het veld vertelt je wat de kracht zou zijn, áls zich op een bepaald moment op een bepaalde plek een tweede geladen voorwerp zou bevinden. Zo is ook dit veld dus een functie van plaats en tijd. De richting van de kracht hangt af van de sterkte van het veld en de lading van het hypothetische tweede voorwerp: een positief geladen voorwerp en een negatief geladen voorwerp trekken elkaar aan, terwijl twee voorwerpen met gelijksoortige lading (beide positief of beide negatief) elkaar juist afstoten. Op vergelijkbare wijze beschrijft een magnetisch veld de kracht die een magneet uitoefent op andere magneten en bewegende elektrische ladingen die in het veld aanwezig zouden kunnen zijn.
Kranen en afvoerputjes
In tegenstelling tot het waterstromingsveld, zien we bij elektrische en magnetische velden niet daadwerkelijk ‘iets’ stromen. Gelukkig kunnen we een redelijke intuïtie krijgen voor de Maxwellvelden door erover na te denken alsof ze wél gewoon de stroming van water beschrijven. Deze analogie is bijzonder nuttig om twee elementen uit de Maxwellvergelijkingen beter te begrijpen, namelijk divergentie en rotatie.
In mijn studentenkamer had ik geen vaatwasser, dus deed ik dagelijks de afwas met de hand. Het water moest altijd eerst even opwarmen, dus zette ik de kraan open, waarbij het water in de gootsteen viel en door het afvoerputje stroomde. Zoals je hierboven zag, kunnen we deze stroming van water in de gootsteen beschrijven met een vectorveld. Dat ziet er ongeveer uit als in de afbeelding hieronder. We zien dat er op bepaalde plekken in de gootsteen (onder de kraan) steeds water wegstroomt, terwijl er naar andere plekken (het afvoerputje) steeds water toe blijft stromen. Het ‘ergens naartoe of vandaan stromen’ van het vectorveld wordt beschreven door de divergentie. Als de divergentie van het veld op een bepaalde plek een positief getal is, dan stroomt er meer water weg van die plek dan ernaartoe. Als de divergentie een negatief getal is, stroomt er juist meer water naar de plek toe dan dat ervandaan. Als ik de kraan openzet, heeft de plek onder de kraan dus een positieve divergentie, en het afvoerputje een negatieve divergentie. Op andere plekken in mijn wasbak stroomt er evenveel water in als uit, en is de divergentie dus gelijk aan nul.
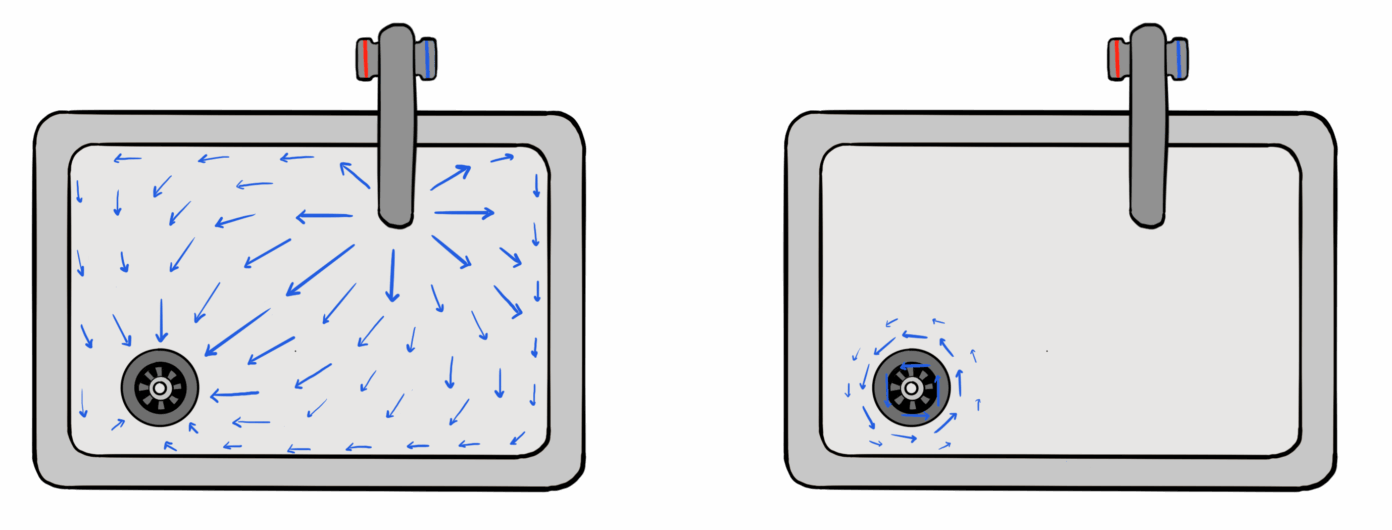
Na de afwas haal ik de stop uit het afvoerputje. Wat er dan gebeurt, heb je misschien zelf ook wel eens gezien: het water stroomt niet in een rechte lijn weg, maar in een soort draaikolkbeweging! De rotatie van een vectorveld beschrijft precies deze draaibeweging. In tegenstelling tot de divergentie, is de rotatie van een vectorveld zelf ook een vector met een grootte en een richting. De richting van de rotatievector beschrijft de as waaromheen het veld roteert, in dit geval een denkbeeldige satéprikker in het midden van mijn afvoerputje. De grootte van de rotatievector beschrijft hoe snel het water om deze as stroomt, en de richting van de vector beschrijft de draairichting: als het water tegen de klok in stroomt, dan wijst de rotatievector omhoog. Als het water met de klok mee stroomt, wijst de rotatievector omlaag.
In wiskundesymbolen wordt zowel de divergentie als de rotatie weergegeven met een driehoek op z’n kop: \( \nabla \), een symbool dat ook wel ‘nabla’ wordt genoemd. De divergentie wordt afgebeeld als nabla met een puntje erachter, de rotatie als nabla met een kruisje erachter1.
Vier combinaties, vier vergelijkingen
Tijd om terug te keren naar Maxwell. Eerder in dit artikel kon je lezen dat er twee soorten vectorvelden centraal staan: elektrische en magnetische velden. Combineer je die met de twee eigenschappen divergentie en rotatie, dan krijg je vier mogelijke combinaties – precies de vier eigenschappen die door Maxwells vergelijkingen worden beschreven. In formulevorm zien de vergelijkingen er ongeveer zo uit:
‘Divergentie/rotatie van elektrisch/magnetisch veld = …’
Wat er op de puntjes komt, verschilt per vergelijking, maar dit patroon vormt de basis van Maxwells theorie.
In wiskundige vergelijkingen wordt het elektrisch veld vaak weergegeven met de letter ‘E’ en het magnetisch veld met de letter ‘B’. De ‘D’ en ‘H’ in de afbeelding bovenaan het artikel zijn gelijk aan het elektrisch en magnetisch veld op vermenigvuldiging met een constante factor na2.
De wet van Gauss
De eerste van de vier Maxwellvergelijkingen beschrijft de relatie tussen elektrische ladingen en elektrisch velden. Zoals eerder in dit artikel al besproken, is het elektrisch veld gerelateerd aan de kracht die een geladen voorwerp uitoefent op andere geladen voorwerpen. De grootte en richting van deze kracht hangen af van de lading van beide voorwerpen, en zijn dus erg situatieafhankelijk. Elektrische velden beschrijven de potentiële invloed van geladen voorwerpen op hun omgeving op een abstractere, maar meer algemene manier, die onafhankelijk is van de eventuele aanwezigheid van andere geladen voorwerpen. Zo’n beschrijving is in het bijzonder erg handig in ingewikkeldere situaties met meer dan twee geladen voorwerpen.
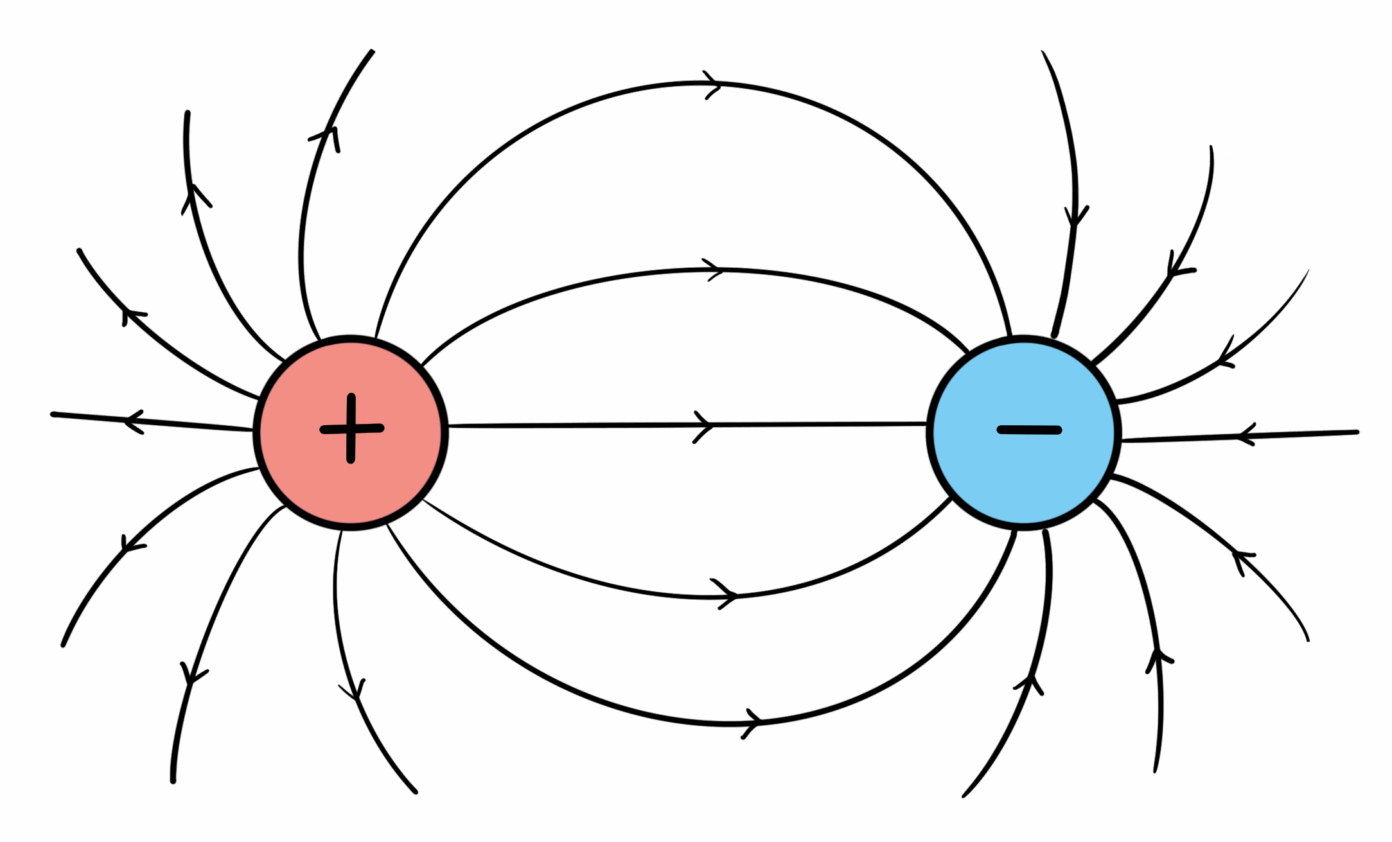
Het elektrisch veld van een geladen voorwerp is zo gedefinieerd dat het overeenkomt met de kracht die een positief geladen ‘testdeeltje’ ervaart als gevolg van die lading. Dat betekent dat het elektrisch veld ‘wegstroomt’ van positief geladen voorwerpen (die stoten het testdeeltje af), en naar negatief geladen voorwerpen ‘toestroomt’ (die trekken het testdeeltje aan). Positieve lading kun je dus vergelijken met een kraan, en negatieve lading met een afvoerputje. Hoe groter de lading, hoe krachtiger de stroming, oftewel: hoe sterker het elektrisch veld. De eerste wet van Maxwell vat dit samen in een wiskundige vergelijking. In woorden luidt deze vergelijking:
‘De divergentie van het elektrisch veld op een bepaalde plek is evenredig met de dichtheid van elektrische lading op die plek.’
Of in wiskundesymbolen:
\( \nabla \cdot D = \rho.\)
De \(\rho\) aan de rechterkant van de vergelijking geeft de dichtheid van de elektrische lading weer. De term ‘evenredig’ betekent dat de divergentie en de ladingsdichtheid gelijk zijn op vermenigvuldiging met een positieve constante factor na. Je kunt in deze wet dus meteen terugzien dat positieve lading zorgt voor positieve divergentie van het elektrisch veld, en negatieve lading voor negatieve divergentie. De vergelijking wordt vaak de wet van Gauss genoemd, naar wiskundige Carl Friedrich Gauss, hoewel de vergelijking eerder al was opgeschreven door Joseph-Louis Lagrange.
Nóg een wet van Gauss
De tweede wet van Maxwell lijkt veel op de eerste, maar dan voor een magnetisch veld. De vergelijking wordt dan ook wel eens weinig origineel de wet van Gauss voor magnetisme genoemd. Vergelijkbaar met het elektrisch veld, beschrijft een magnetisch veld de kracht die een magneet uitoefent op andere magneten en op bewegende geladen deeltjes. De rollen van de positieve en negatieve lading worden nu vervuld door de noord- en zuidpolen van magneten en daartussen ‘stroomt’ het magnetisch veld. Een belangrijk verschil is dat er – voor zover bekend – geen magnetische monopolen bestaan: losse noord- of zuidpolen zijn nog nooit waargenomen.

Iedere magneet heeft dus zowel een noord- als een zuidpool, en het magnetisch veld ‘stroomt’ langs gekromde trajecten tussen die polen: buiten de magneet van de noord- naar de zuidpool, en binnen de magneet precies andersom. Op iedere plek ‘stroomt’ er dus evenveel in als uit. Je kunt nu misschien wel raden dat de tweede wet van Maxwell dit samenvat als:
‘De divergentie van het magnetisch veld is overal gelijk aan nul.’
Oftewel,
\( \nabla \cdot B = 0. \)
Als er ooit wél een magnetische monopool wordt waargenomen, dan moet deze vergelijking worden aangepast. In dat geval zou de tweede Maxwellvergelijking er exact hetzelfde uitzien als de eerste met het elektrisch veld en de elektrische lading vervangen door hun magnetische tegenhangers.
De wet van Faraday
De eerste twee Maxwellvergelijkingen beschrijven eigenschappen van óf het elektrisch veld óf het magnetisch veld, maar je kon eerder al lezen dat elektriciteit en magnetisme geen onafhankelijke fenomenen zijn. De derde en vierde wet van Maxwell beschrijven de verbanden tussen elektrische en magnetische velden. In woorden luidt de derde Maxwellvergelijking of wet van Faraday
‘De rotatie van het elektrisch veld is gelijk aan (min) de verandering van het magnetisch veld in de tijd.’
‘Verandering in de tijd’ wordt in wiskundesymbolen opgeschreven als de afgeleide naar de tijd, en in formulevorm ziet de derde Maxwellvergelijking er dus als volgt uit.
\(\nabla \times E = – \frac{\partial B}{\partial t}.\)
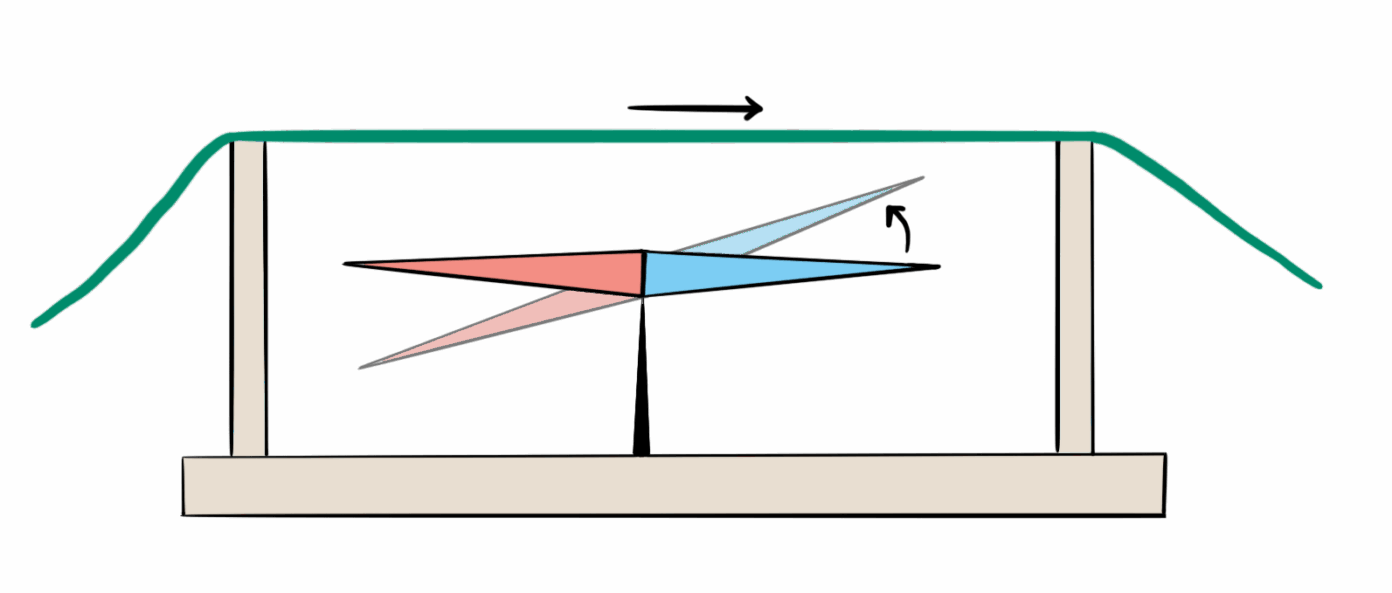
Wat dit concreet betekent, is dat een verandering van het magnetisch veld een roterend elektrisch veld met zich meebrengt. Zo’n verandering wordt bijvoorbeeld veroorzaakt door het verplaatsen of roteren van een magneet.
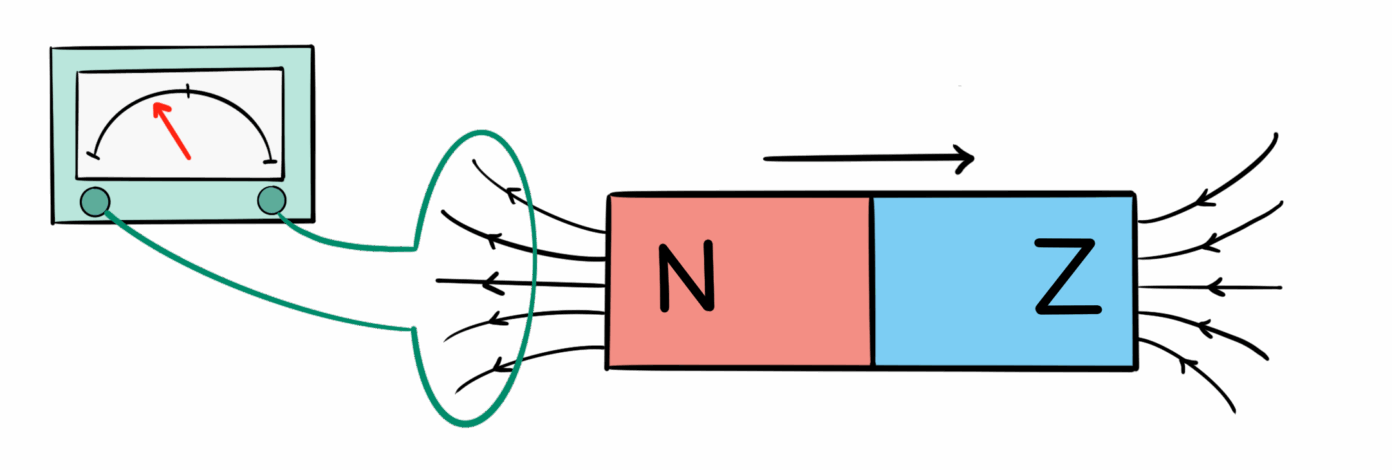
In het bijzonder kan met de derde wet van Maxwell een verklaring worden gegeven voor de door Faraday ontdekte elektromagnetische inductie, het verschijnsel waarbij een veranderend magnetisch veld zorgt voor de opwekking van een elektrische stroom. Dit fenomeen treedt bijvoorbeeld op als je een magneet heen en weer beweegt in de buurt van een elektrisch circuit. De beweging van de magneet veroorzaakt een verandering van van het magnetisch veld: het veld is sterker als de magneet dichterbij is. Volgens de derde wet van Maxwell gaat dit gepaard met een roterend elektrisch veld. Het elektrisch veld – of om precies te zijn: de elektrische kracht die door dit veld wordt beschreven – zorgt ervoor dat elektronen in het elektrisch circuit gaan bewegen, oftewel dat er een stroom loopt!
De wet van Ampère en Maxwell
Waar de bijdrage van Maxwell aan de eerste drie wetten vooral bestaat uit het samenbrengen van de verschillende fenomenen in één beschrijving, had hij een groter aandeel in de laatste wet. Deze wet is gebaseerd op het werk van Ampère, die elektrische stroom relateerde aan magnetische kracht. Hiermee gaf Ampère een verklaring voor de observaties van Ørsted, waarmee de stroom aan ontdekkingen over elektromagnetisme was begonnen.
Maxwell breidde de wet van Ampère uit om ook met veranderende elektrische stromen rekening te kunnen houden. Het resultaat lijkt erg op de wet van Faraday met de rollen van het elektrisch en magnetisch veld omgedraaid, maar bevat een extra term die de elektrische stroom beschrijft:
‘De rotatie van het magnetisch veld is evenredig met de som van de dichtheid van elektrische stroom en de verandering van het elektrisch veld in de tijd.’
De dichtheid van elektrische stroom wordt weergegeven met de letter ‘J’, en de wiskundige vergelijking ziet er dus als volgt uit.
\( \nabla \times H = \frac{\partial D}{\partial t} + J.\)
Met Maxwells toevoeging aan de wet van Ampère was het plaatje compleet, en was er voor het eerst één krachtig raamwerk dat elektriciteit en magnetisme verenigde.
De invloed van Maxwell
Maxwells vergelijkingen bleken niet alleen een samenvatting van bestaande kennis, maar openden ook de deuren naar nieuwe ontdekkingen. Zo leidde Maxwell zelf in 1865 de golfvergelijking van elektromagnetische golven af. Deze vergelijking beschrijft de voortplanting van elektrische en magnetische velden door de ruimte. In het bijzonder kunnen elektromagnetische golven zichzelf in stand houden door de wisselwerking tussen elektrische en magnetische velden: als ze eenmaal bestaan, is er geen lading meer nodig om de golven in stand te houden. De snelheid van de golven bleek overeen te komen met de lichtsnelheid, waaruit Maxwell de verrassende conclusie trok dat licht een elektromagnetische golf is.
Met zijn werk legde Maxwell de basis voor grote natuurkundige doorbraken in de 20e eeuw, en in het bijzonder voor Einsteins speciale relativiteitstheorie. Tijdens een bezoek van Einstein aan de universiteit van Cambridge, zei iemand tegen Einstein dat hij grote ontdekkingen had gedaan, omdat hij op de schouders van Newton stond. Einstein antwoordde hierop: ‘Nee, ik stond op de schouders van Maxwell.’ Ook vandaag, ruim anderhalve eeuw na het werk van Maxwell, behoren de vergelijkingen nog tot de fundamenten van de natuurkunde, en zijn ze minstens net zo relevant als op de dag dat Maxwell ze opschreef.
[1] Voor wiskundekenners: de nabla kan zelf ook worden gezien als een vector. Met het puntje wordt het inproduct tussen nabla en het vectorveld bedoeld, met het kruisje het kruisproduct.
[2] Deze eenvoudige relaties tussen de vectorvelden zijn alleen waar in een perfect vacuüm, dat wil zeggen: zonder materie. In realistischere situaties zijn de Maxwellvergelijkingen zoals in de afbeelding bovenaan het artikel nog steeds geldig, maar zijn de relaties tussen ‘E’ en ‘D’ en tussen ‘B’ en ‘H’ ingewikkelder.