
In the context of quantum gravity, theoretical physicists, including for example Stephen Hawking, have been trying to exploit the emergence of these simple mathematical statements to ponder about the, yet unknown, microscopic theory of quantum gravity. You can think of this as analogous to inspecting the phenomenon of temperature to study the existence of particles.
In this third part of our series about approaches to quantum gravity, we are going to dive into Euclidean quantum gravity. This approach tries to effectively describe the features of quantum gravity on a scale much larger than its fundamental building blocks. By definition such an approach is not a complete description of quantum gravity, but it may reveal the paths towards the right ideas and concepts needed to fully capture the features of quantum gravity. Let us continue this tour by going through the good, the bad and the ugly of Euclidean quantum gravity!
The good: Thermodynamics, singularities and information recovery
Usually we think of time as stretching out indefinitely, but in Euclidean quantum gravity we effectively treat time as a compact dimension, which loops around a circle. Surprisingly, this leads to many resolutions to problems concerning black holes. One can achieve such a compact time dimension after multiplying time with the imaginary number \( i \) as follows
\( t_E=it \),
where \( t_E \) is called the Euclidean time and \( t \) is the usual time.
By applying this formula to the case of black holes, physicists immediately find two astonishing features: black holes radiate at the Hawking temperature and the singularity of the black hole is not present! This is incredible, since physicists know that the singularity found in the center of the black hole in other theories is an unphysical point, a remnant of the fact that general relativity cannot describe quantum effects, whereas here one finds that it magically vanishes. Equally impressive is the fact that this framework predicts Hawking radiation by requiring the geometry around the black hole horizon to be smooth1.
One might wonder: if Euclidean quantum gravity can explain the origin of Hawking radiation and how the singularity disappears, might it also tell us something about the black hole information paradox? The short answer: yes! The long answer is a bit more nuanced. Physicists have found that when one studies gravity on a 2-dimensional plane (instead of our 4-dimensional world), one can restore the information in terms of the most sci-fi objects to date: wormholes! These wormholes arise through complex mathematical tools, including the use of Euclidean quantum gravity. For a longer discussion of this particular finding I refer to the article: `Has the black hole information paradox evaporated?´ on the Symmetry Magazine website.
With all these benefits and resolutions to paradoxes (at least in idealized situations), what could possibly go wrong?
The bad: Causality
One of the most important concepts present in the theory of relativity is the notion of causality. In our everyday life we identify causality as “something happening because of something else”, meaning we recognize that two events can or cannot influence each other. The German mathematician Hermann Minkowski taught us that the way to describe causality is in terms of the spacetime interval. The spacetime interval is nicely captured by the light cone.
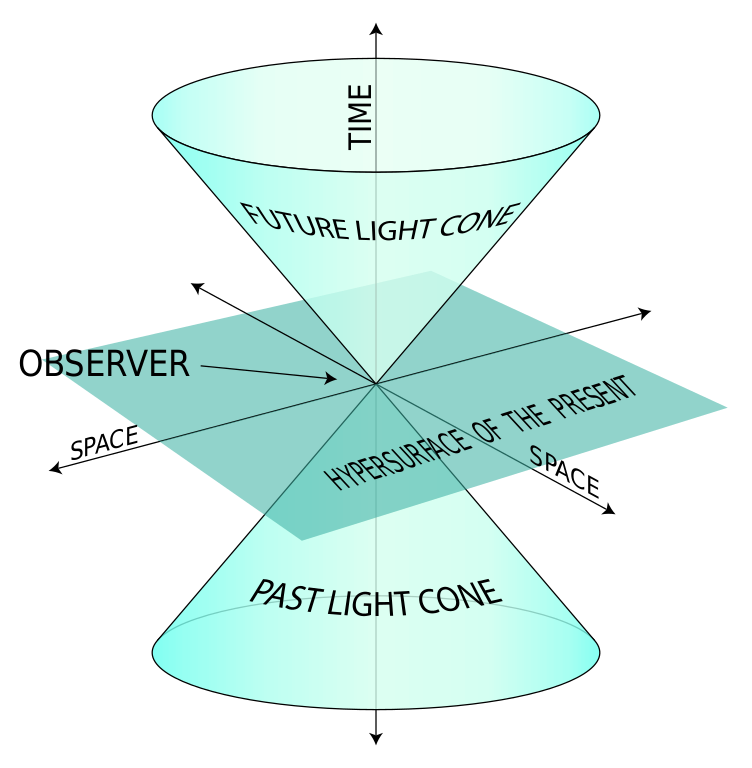
Anything that happens inside the light cone is in causal contact with whatever happens at its apex. At least, that is the case in ‘normal’ relativity. When we look at the Euclidean spacetime we find that this notion of the light cone gets lost and we are no longer able to describe how events influence each other. In other words: we have lost the notion of causality in Euclidean quantum gravity.
The ugly: Unboundedness from below
Another property of the Euclidean method is that instead of thinking about quantum mechanical tunneling we can think of simple motion along hills. Let me explain. We can imagine a position-dependent potential energy of the following shape:
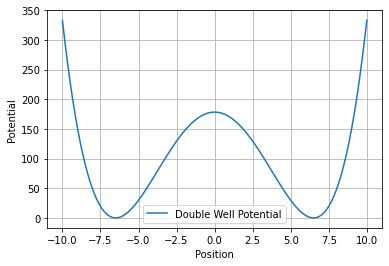
Inside this ‘potential energy landscape’ we may find a particle being trapped at the bottom of one of the two wells, which are embedded inside the bigger walls. These two points are the points of the particle’s lowest energy. To roll it up the hill we need to push the particle with some energy. Quantum mechanically speaking, there is also a probability that the particle can tunnel through the smaller middle hill to the other well, even if it ‘classically’ does not have enough energy to do so. We can also describe this behavior by investigating the potential in Euclidean time. Interestingly enough, the potential then turns out to gain an overall minus sign and as such now looks as follows:
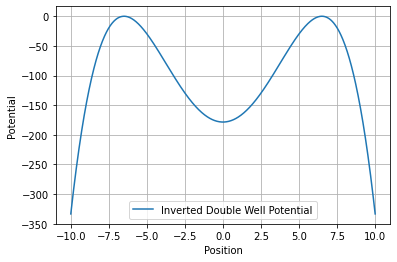
Now the hill became a well and the wells became hills, meaning that the quantum tunneling process is now just rolling down and up a hill! This is great: quantum effects are encapsulated by simple motion in Euclidean time.
But how is all of this bad or even ugly? Well, it has to do with energy, more precisely, the lowest energy state. In the first case we found the wells to be the lowest energy states, but in Euclidean time we find that if the particle does not roll towards the middle, but towards the slopes at the edges, it will reach an energy of \( E=-\infty \). This is horrible as it would mean that the lowest energy state is one of negative infinite energy! Due to the fact that it goes indefinitely towards the bottom we call this behavior unboundedness from below.
Good, bad or ugly?
There is no doubt that Euclidean quantum gravity provides some correct descriptions of the quantum features we expect gravity to have. However, it is still unclear what the complete picture of quantum gravity will entail. At the BBC Reith Lectures, Stephen Hawking once said:
…black holes […] are not the eternal prisons they were once envisaged. […] So, if you feel you are in a black hole, don’t give up – there’s a way out.
In the spirit of Stephen Hawking, physicists will not give up, continue to iron out the problems that arise, and try to push further the features we gather from Euclidean quantum gravity to unlock the nature of quantum gravity. So let us continue on our path towards the mysteries behind space and time!
[1] Note that this smoothness is different from the one found at the singularity before the ‘euclideanization’. This is a very technical point and not relevant for the discussion.