De zwaartekracht in de hogerdimensionale theorie leidde namelijk niet alleen tot onze zwaartekracht, maar veroorzaakte ook een elektromagnetische kracht. Dit maakt het toevoegen van extra dimensies tot een ingenieuze methode om de fundamentele krachten te verenigen, een nuttig hulpmiddel in de zoektocht naar een ‘theorie van alles’.
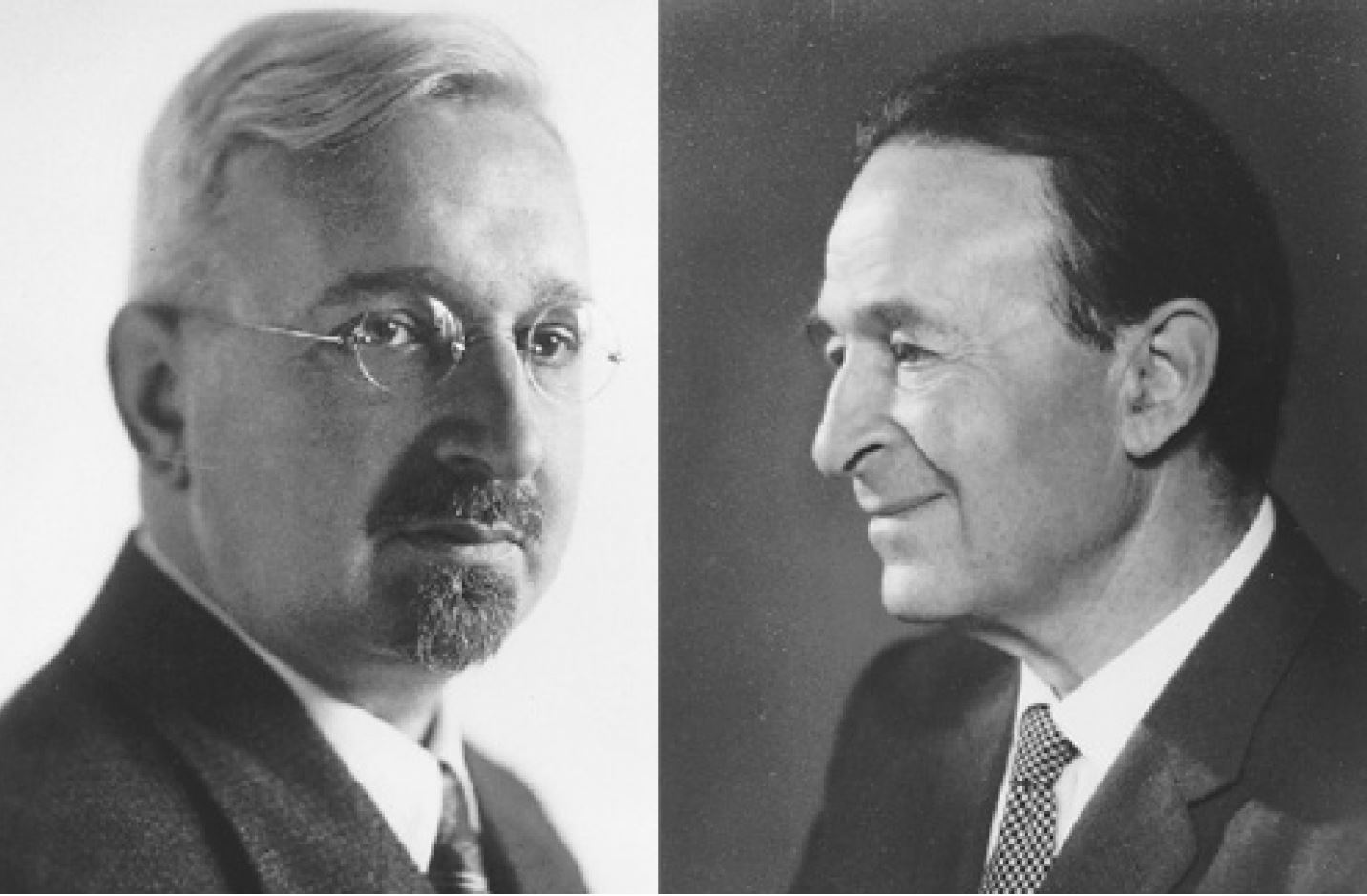
Een idee wordt geboren
In 1919, vier jaar nadat Einstein zijn algemene relativiteitstheorie had gepresenteerd, bestudeerde de Duitse natuurkundige Theodor Kaluza hoe Einsteins theorie zou werken als onze ruimte een dimensie meer zou hebben. Wijzelf leven in een vierdimensionale wereld: drie voor ruimte en één voor tijd. Kaluza formuleerde relativiteitstheorie in een vijfdimensionale ruimtetijd – eerst puur uit wiskundige interesse. Op zichzelf verschilt het toepassen van relativiteitstheorie in andere aantallen dimensies niet echt van hoe dat werkt in onze vierdimensionale ruimtetijd. Het was dus zeer verrassend toen Kaluza de wetten van relativiteitstheorie in vijf dimensies projecteerde naar onze vierdimensionale ruimtetijd, en daarbij niet alleen de zwaartekracht maar ook de elektromagnetische kracht vond. Aangemoedigd door Einstein werkte Kaluza dit idee uit in een artikel. Ook Einstein zelf zou later nog aan dit onderwerp gaan werken.
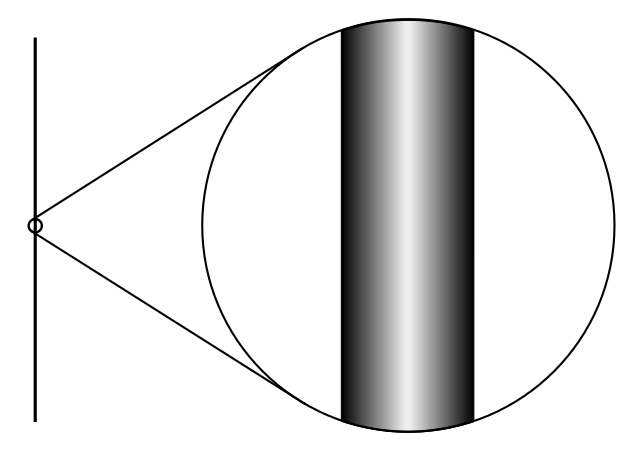
Op een wiskundig niveau klopte deze afleiding, maar een interpretatie van de extra dimensie ontbrak nog. Kaluza kon niet zo goed verklaren waarom we deze extra dimensie niet zien, maar Oskar Klein gaf hier in 1926 wel een antwoord op. Hij stelde voor dat de extra dimensie niet oneindig uitgestrekt is, zoals onze vierdimensionale ruimtetijd dat wel is, maar opgerold tot een hele kleine cirkel, zo klein dat we hem niet kunnen zien. Om ons dit beter voor te kunnen stellen, kunnen we kijken naar een eenvoudiger voorbeeld. Laten we de vijfdimensionale ruimtetijd vervangen door een gespannen koord. Voor een koorddanser die naar de overkant probeert te lopen is het koord eendimensionaal, want hij kan alleen voor- of achteruit lopen. Maar voor mieren of andere kleine insecten is het koord tweedimensionaal, want zij kunnen ook rondom het koord lopen. Oftewel: afhankelijk van ons perspectief is het koord effectief één- of tweedimensionaal. Precies dit is het idee van Klein, alleen dan in het hogerdimensionale geval van vier- en vijfdimensionale ruimtetijden. De opgerolde dimensie is alleen zichtbaar op de allerkleinste schaal.
Algemene relativiteitstheorie en metrieken
Om te begrijpen hoe we vierdimensionaal elektromagnetisme terug kunnen vinden in vijfdimensionale zwaartekracht, moeten we de werking van relativiteitstheorie eerst iets beter begrijpen. Een centrale vraag in de algemene relativiteitstheorie is hoe we de afstand tussen twee punten in de ruimtetijd meten. Hiervoor gebruiken natuurkundigen (en wiskundigen) een zogenaamde metriek, en het is precies deze metriek waarin we het elektromagnetisme zullen terugzien. Voordat we afstanden via deze metrieken gaan definiëren, is het echter leerzaam om eerst na te gaan hoe we dat in het simpele geval van een plat tweedimensionaal vlak zouden doen. Stel dat we iets over een afstand a in de x-richting en een afstand b in de y-richting verplaatsen. Dan vertelt de stelling van Pythagoras ons dat het kwadraat van de afstand gegeven is door
\( c^2 = a^2+b^2\).
Als de x– en y-richtingen niet loodrecht op elkaar staan maar onder een hoek \(\theta\) (zie afbeelding 3 hieronder), dan kan de afstand (met behulp van SOS-, CAS- en TOA-regels) worden geschreven als
\( c^2 = a^2+b^2 -2 ab \cos(\theta)\).
Maar hoe werkt de berekening van deze afstand nu precies via metrieken? We kunnen de metriek zien als een hulpmiddel dat ons vertelt welke lengteschalen we met alle richtingen associëren. In het meest algemene geval zou dit er voor het tweedimensionale vlak uitzien als
\( c^2 = g_{xx} a^2 + g_{yy} b^2 + g_{xy} ab + g_{yx} ba\),
waarbij we de coefficiënten g samen de metriek noemen. De metriek heeft dus verschillende componenten, gelabeld door de richtingen x en y, waarbij de onderindex x of y in g precies overeenkomt met vermenigvuldiging met de verplaatsing a of b in die richting. Daarbij moet de metriek ook symmetrisch zijn, in de zin dat \(g_{xy}=g_{yx} \). In meer wiskundige termen kun je ook wel zeggen dat de metriek dus een symmetrische matrix is, die geschreven kan worden als
\(g = \begin{pmatrix} g_{xx} & g_{xy} \\ g_{yx} & g_{yy} \end{pmatrix}\).
Nu kunnen we de afstandsberekeningen hierboven reproduceren simpelweg door voor de componenten van g waardes invullen. Voor het platte vlak waarbij de x– en y-richting loodrecht op elkaar staan kiezen we\(g_{xx}=g_{yy}=1\) en \( g_{xy}=g_{yx}=0 \). Maar we hadden ook onze verplaatsing in de x- en y-richting met andere lengteschalen kunnen meten, en daardoor andere waardes voor \(g_{xx}\) en \(g_{yy}\) kunnen invullen. Bijvoorbeeld \(g_{xx}=1\) en \(g_{yy}=10.000\) als we de verplaatsing in de x-richting in meters meten, en in de y-richting in centimeters. (Een meter bevat 100 centimeter, maar de metriek bepaalt het kwadraat van de afstand, vandaar de factor 10.000.) Ook de hoek tussen de x– en y-richting die we hierboven kozen heeft een natuurlijke interpretatie in termen van de metriek: die geeft kruistermen door \( g_{xy}=g_{yx}=-\cos(\theta)\). Dit alles maakt de metriek tot een elegant hulpmiddel om afstanden op een algemene manier te beschrijven, zonder noodzaak om van tevoren handige loodrechte assen met een vaste afstandsmaat te kiezen.
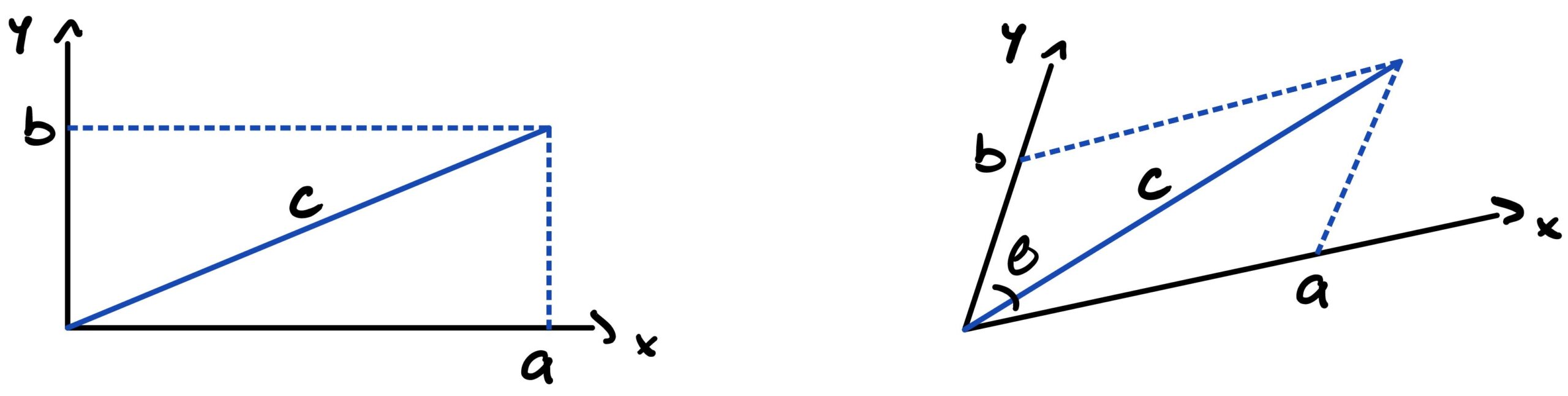
Voor eenvoudige voorbeelden zoals het platte vlak klinkt het introduceren van een metriek misschien wat omslachtig, maar voor de ruimtetijden die in algemene relativiteitstheorie worden bestudeerd komen ze goed van pas. Ben je bijvoorbeeld vlak bij een zwart gat, dan zul je afstanden op een andere manier waarnemen dan gewoon hier op Aarde. Voor iedere plek in ruimtetijd zouden we zo een nieuw assenstelsel moeten bouwen als we via de stelling van Pythagoras afstanden zouden willen berekenen. Gebruiken we daarentegen een metriek, dan hoeven we alleen maar iets andere waardes voor de componenten van g in te vullen. Daarbij kunnen ook de Einstein-vergelijkingen – de wetten van algemene relativiteitstheorie – opgeschreven worden in termen van g. Door deze vergelijkingen vervolgens op te lossen voor de individuele componenten van g kunnen we beschrijven hoe onze ruimtetijd eruit ziet, zowel hier op Aarde als in de buurt van de horizon van zwarte gaten.
Metrieken en extra dimensies
Als we nu een metriek voor een vijfdimensionale ruimtetijd willen opschrijven in plaats van voor het tweedimensionale vlak, betekent dat dat de labels van g vijf verschillende waardes kunnen aannemen in plaats van twee. Er zijn nu immers vijf richtingen waarin we kunnen verplaatsen (als je ‘verplaatsen in de tijd’ ook meetelt), waar er dat hiervoor maar twee waren. Dit betekent dat de metriek nu \( 5 \times 5 =25 \) componenten heeft in plaats van \( 2 \times 2 =4 \). Deze componenten kunnen compact samengebundeld worden tot
\(g = \begin{pmatrix} g_{11} & g_{12} & g_{13} & g_{14} & g_{15} \\ g_{21} & g_{22} & g_{23} & g_{24} & g_{25} \\ g_{31} & g_{32} & g_{33} & g_{34} & g_{35} \\ g_{41} & g_{42} & g_{43} & g_{44} & g_{45} \\ g_{51} & g_{52} & g_{53} & g_{54} & g_{55} \end{pmatrix}\).
De componenten gelabeld met 1 t/m 4 beschrijven nu de vierdimensionale ruimtetijd waarin wij leven, terwijl de componenten \(g_{15}, g_{25}, g_{35}, g_{45}, g_{55}\) (en hun symmetrische partners) nieuwe parameters in onze theorie zijn. Die theorie is vijfdimensionaal, maar als we nu aannemen dat één dimensie heel klein opgerold is blijven er vier dimensies over. Welke rol spelen de extra parameters in die vierdimensionale theorie? Als je de Einstein-vergelijkingen voor vier van de vijf parameters, namelijk \(g_{15}, g_{25}, g_{35}, g_{45}\), zou uitschrijven, dan vinden we vergelijkingen die verdacht veel lijken op de wetten van elektromagnetisme. Dit was precies wat Kaluza toentertijd opviel, en hoe hij beredeneerde dat zwaartekracht in vijf dimensies resulteerde in zwaartekracht en elektromagnetisme in vier dimensies. De parameters \(g_{15}, g_{25}, g_{35}\) en \(g_{45}\) worden hierbij gebruikt om het gedrag van fotonen, de fundamentele deeltjes van de elektromagnetische interactie, te beschrijven.
Daarbovenop is er ook nog de component \(g_{55}\) die nóg een extra parameter toevoegt aan de vierdimensionale theorie. In vijf dimensies kan deze parameter geïnterpreteerd als een maat voor de grootte van de cirkel, aangezien een verplaatsing in de vijfde richting vermenigvuldigd wordt met \(g_{55}\) als we de afstand bepalen. In vier dimensies blijkt dat deze parameter vervolgens een natuurlijke fysische interpretatie zou moeten hebben – \(g_{55}\) komt namelijk overeen met een nieuw hypothetisch deeltje, genaamd het dilaton. Elektromagnetisme kennen we al, maar een dilaton is tot dusver nog nooit waargenomen. Detectie van dit deeltje in een deeltjesversneller zou dus een goede hint zijn dat we daadwerkelijk in een universum met extra opgerolde dimensies leven.
Kortom, de theorie van Kaluza en Klein geeft een interessante manier om over ons universum na te denken. Misschien leven wij wel helemaal niet in vier dimensies, maar zijn er extra dimensies die zo klein zijn opgerold dat we ze niet kunnen zien. Op zichzelf klinkt dit natuurlijk vooral als een wilde speculatie, maar het geeft ook een ingenieuze methode om in vier dimensies de zwaartekracht met de elektromagnetische kracht te verenigen tot een vijfdimensionale zwaartekracht. Door elegante technieken zoals metrieken te gebruiken blijkt maar weer eens dat wiskunde ons overkoepelende raamwerken geeft om natuurkunde mee te beschrijven. Of ons eigen universum daadwerkelijk opgerolde dimensies heeft blijft voorlopig een vraag, maar misschien dat deeltjesdetectoren daar in de toekomst een antwoord op kunnen geven.