Het casimireffect

Zet twee metalen platen zonder elektrische lading dicht bij elkaar in een vacuüm. In eerste instantie zou je dan misschien verwachten dat de platen stil blijven staan: er is bijvoorbeeld geen magnetische aantrekkingskracht die tussen deze platen werkt. Wat echter blijkt is dat een quantummechanisch effect – het zogenaamde casimireffect – ervoor zorgt dat de platen toch naar elkaar toe bewegen! De oorsprong van dit effect ligt in het feit dat het vacuüm vanuit een quantummechanisch perspectief helemaal niet zo leeg is als het lijkt. Hoe dit precies werkt zal ik in dit artikel ophelderen.

Het casimireffect werd in 1947 al voorspeld als een kracht tussen geleidende platen door de Nederlandse natuurkundigen Hendrik Casimir en Dirk Polder. Een jaar later werkte Casimir zelf de theorie achter de ontdekking uit, na een gesprek over de energie van het vacuüm met Niels Bohr, een van de pioniers in de quantummechanica. In de praktijk bleek het echter lastig om de aantrekkingskracht tussen geleidende platen waar te nemen, en pas in 1997 lukte het Steve Lamoureaux om het casimireffect overtuigend experimenteel te bevestigen.

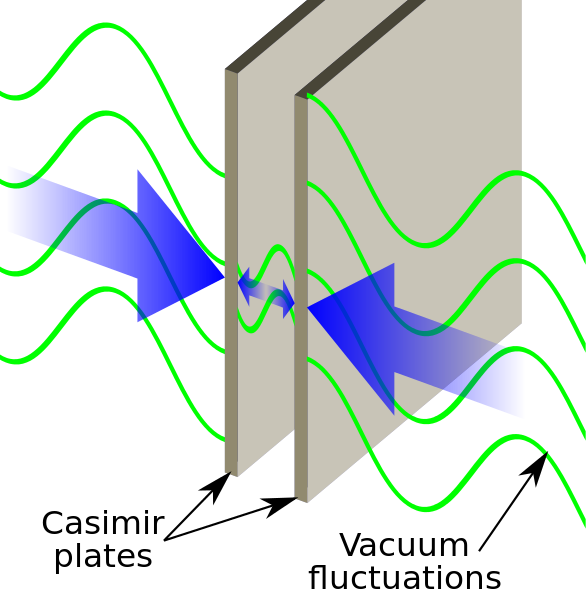
Hoe werkt het casimireffect nu precies? Om dit uit te kunnen leggen moeten we eerst de eigenschappen van het vacuüm in quantummechanica beter begrijpen. De energie van het vacuüm, de zogenaamde nulpuntsenergie, speelt namelijk een belangrijke rol in het casimireffect. Het idee is dat het vacuüm in quantummechanica helemaal niet zo leeg is als je zou denken, maar dat er ook in de helemaal lege ruimte nog steeds golven fluctueren. Deze golven worden quantumfluctuaties genoemd. Ze zorgen ervoor dat de energie van het vacuüm niet precies nul is, maar een bijdrage krijgt van deze quantumfluctuaties.

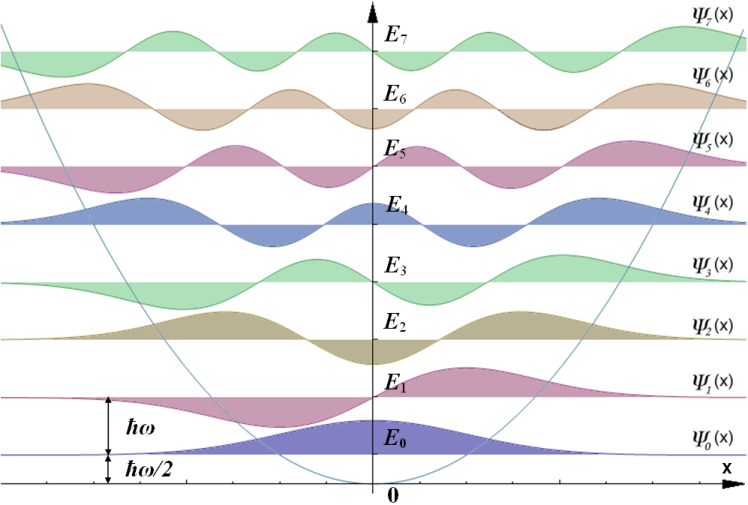
Een voorbeeld waarin we deze eigenschappen van het vacuüm al kunnen terugzien is de harmonische oscillator. Binnen de klassieke mechanica komen we harmonische oscillatoren vaak tegen, bijvoorbeeld wanneer we naar de trillingen van snaren kijken, maar ook in de quantummechanica komen dit soort systemen voor. Een harmonische oscillator is een regelmatig trillend systeem dat wordt gekenmerkt door een bepaalde frequentie \(\omega\). Voor een klassieke harmonische oscillator zoals een trillende snaar komen de verschillende mogelijke toestanden van het systeem vervolgens overeen met de grond- en boventonen van deze snaar. Binnen de quantummechanica heeft een harmonische oscillator ook verschillende toestanden, met wederom vaste energieën die we kunnen uitdrukken als

\(E_n = \hbar \omega (n + \frac{1}{2} ),\)

waarbij \( \hbar\) de constante van Planck is, en \(n\) een geheel getal dat de toestanden ‘telt’. Hieruit volgt dat de nulpuntsenergie \(E_0 = \hbar \omega / 2\) de energie van het vacuüm is – en dat die dus inderdaad niet gelijk is aan 0. Vaak kunnen we de energie \(E_0\) voor de vacuümtoestand van fysische systemen negeren, omdat we meestal alleen het verschil in energie tussen bepaalde toestanden willen weten – bijvoorbeeld omdat we willen weten hoeveel energie er vrijkomt als een systeem van de ene naar de andere toestand gaat, of hoeveel energie zoiets juist kost. Voor het casimireffect kunnen we daarentegen het begrip van nulpuntsenergie wél gebruiken, om de aantrekkende kracht tussen twee ongeladen metalen platen te verklaren.

We kunnen namelijk het casimireffect begrijpen door de quantumfluctuaties rondom de platen te beschrijven als harmonische oscillatoren. Als opstelling kijken we naar twee platen die van elkaar af staan op een bepaalde afstand, die we \(d\) zullen noemen. De fluctuaties kunnen zich nu op twee plaatsen bevinden, namelijk tussen de platen in of erbuiten. Laten we voor het gemak zeggen dat dit gehele systeem zich in een doos van lengte \(L\) bevindt, waarbij de platen zich helemaal aan de linkerkant van de doos bevinden, zoals weergegeven in afbeelding 3. Dit betekent dat de quantumfluctuaties of tussen de linker- en de rechterplaat liggen, of tussen de rechterplaat en de rand van de doos. Daarbij kunnen deze fluctuaties niet iedere willekeurige golflengte hebben, maar moeten ze gequantiseerd zijn. De golflengte \(\lambda\) van een fluctuatie tussen de platen moet namelijk precies een geheel aantal keer in dat interval passen, oftewel \(\lambda = d, d/2, d/3, \ldots\), en net zo voor fluctuaties tussen de rechterplaat en de rand van de doos. Deze quantisatie zorgt ervoor dat de quantumfluctuaties nul zijn bij de platen zelf. (De kleine lettertjes: aan die eis is ook voldaan als er een aantal halve golven tussen de platen past – voor het gemak laten we die golven hier verder buiten beschouwing, maar ze dragen op precies dezelfde manier bij aan het casimireffect.) Dit soort eisen op het gedrag van golven op specifieke plekken worden randvoorwaarden genoemd. Ze komen vaker terug binnen de natuurkunde, bijvoorbeeld bij de trillingen van een snaar waarvan de uiteinden vast zitten.

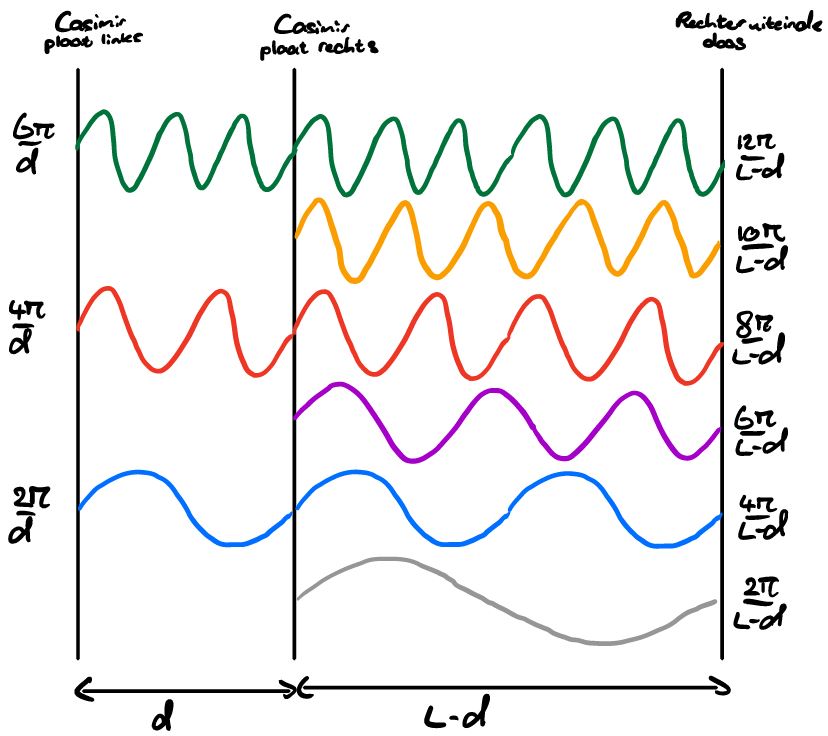
Het idee is nu dat iedere quantumfluctuatie overeenkomt met één harmonische oscillator. We kunnen de frequentie \(\omega\) van deze harmonische oscillatoren uitdrukken in termen van de golflengte \(\lambda\) van de fluctuaties via

\(\omega = 2\pi/\lambda .\)

Voor fluctuaties tussen de platen moesten de golflengtes precies een geheel aantal maal in \(d\) passen, dus de frequenties zijn \(\omega =2\pi/d, 4\pi/d, 6\pi/d, …\). Op eenzelfde manier vinden we dan \(\omega =2\pi/(L-d), 4\pi/(L-d), 6\pi/(L-d), …\) als frequenties voor fluctuaties tussen de rechterplaat en de rand van de doos.

We kunnen vervolgens de energie van ons vacuum bepalen door de nulpuntsenergieën van al deze harmonische oscillatoren op te tellen. Dit levert een enigszins eigenaardige uitdrukking op voor de totale nulpuntsenergie, doordat we een oneindig aantal oscillatoren hebben. Nu zijn er binnen de theoretische natuurkunde technieken ontwikkeld om met dit soort oneindigheden om te gaan – een verzameling technieken die renormalisatie wordt genoemd. Om het casimireffect op een conceptueel niveau te begrijpen hebben we deze technieken echter niet nodig. Als we namelijk naar afbeelding 3 kijken, dan zien we dat een verandering in de afstand \(d\) tussen te platen de nulpuntsenergieën van alle harmonische oscillatoren aanpast. Als we de afstand \(d\) kleiner maken worden de nulpuntsenergieën van fluctuaties tussen de platen groter, terwijl de nulpuntsenergieën van fluctuaties tussen de rechterplaat en de rand van de doos kleiner worden. Dit maakt het al aannemelijk dat de totale nulpuntsenergie ook afhankelijk is van de afstand \(d\), dus schrijven we hiervoor \(E(d)\). En aangezien fysische systemen altijd energie willen minimaliseren, betekent dit dat er dus effectief een kracht tussen de platen werkt wanneer een verandering van de afstand \(d\) een lagere energie oplevert. Om precies te zijn: de kracht \(F\) die op de platen werkt volgt uit de afgeleide van de energie naar deze afstand als

$$F = E’(d).$$

Hieruit kunnen we ook de richting waarin de kracht werkt, oftewel of de kracht aantrekkend of afstotend is, beredeneren. Kijk bijvoorbeeld naar twee geleidende platen die dicht op elkaar staan. Dit betekent dat de afstand \(d\) tussen de platen veel kleiner is dan de grootte \(L\) van de doos, oftewel \(d \ll L\). Als we dan naar de spreiding in de energieniveaus in afbeelding 3 kijken, zien we dat de fluctuaties tussen de platen veel verder uit elkaar liggen dan de fluctuaties buiten de platen. In andere woorden, de energiedichtheid van het vacuüm is tussen de platen lager dan buiten de platen. En aangezien de kracht volgt uit deze energiedichtheden, vinden we dat de kracht waarmee de ertussen liggende fluctuaties de platen naar buiten duwen lager is dan de kracht die van buitenaf werkt, zoals ook schematisch in afbeelding 1 is weergegeven. Oftewel, het casimireffect leidt inderdaad netto tot een aantrekkende kracht tussen de platen. Het argument hierboven is natuurlijk slechts een ruwe schets van hoe het casimireffect in werking treedt, maar deze kracht kan ook precies worden beschreven door middel van de eerder genoemde renormalisatie-technieken.

Kortom, het casimireffect geeft ons een interessant blik op de bijzondere manieren waarop quantummechanica kan werken in vergelijking met klassieke mechanica. De klassieke mechanica vertelt ons namelijk dat ongeladen metalen platen geen krachten op elkaar zouden uitoefenen. (Dat wil overigens niet zeggen dat het casimireffect niet buiten de quantumwereld voorkomt! Ook schepen in het water vlakbij de kade of vlakbij elkaar ervaren een soortgelijk effect, waarbij de watergolven de rol van de quantumfluctuaties spelen.) Quantummechanica zegt dat het vacuüm rondom deze platen helemaal niet leeg is, en dat juist quantummechanische fluctuaties eromheen ervoor zorgen dat de ongeladen metalen platen toch door elkaar kunnen worden aangetrokken. Om de details van dit soort fenomenen te ontrafelen hebben theoretische natuurkundigen ingewikkelde rekenschema’s bedacht, maar de concepten zelf kunnen vaak al begrepen worden door problemen op te delen in simpelere componenten die we al wel snappen, zoals we hier harmonische oscillatoren hebben gebruikt.