Geschiedenis van de wiskunde: een spotlight op de oude niet-Westerse wiskunde
Door Vera Moerbeek
Wat de ontwikkeling van de wiskunde betreft hebben we veel te danken aan de Grieken. De stelling van Thales, de stelling van Pythagoras en de Elementen van Euclides worden nog steeds veel gebruikt in de wiskunde. Er wordt vaak gezegd dat de Griekse wiskunde gedurende de middeleeuwen door wetenschappers in het Midden-Oosten werd bewaard en doorgegeven aan de rest van Europa aan het begin van de renaissance. Wordt hiermee echter niet op Eurocentrische manier nogal wat onder het tapijt geschoven? Veel wetenschappers in het Midden-Oosten hebben zelf ook een significante bijdrage geleverd aan de wiskunde, en we moeten ook zeker de invloed van India en China niet vergeten. In dit artikel delf ik wat dieper in de niet-Westerse geschiedenis van de wiskunde.
Natuurlijk is er een groot debat omtrent ‘wie bedacht wat als eerste’ en ‘wie heeft wie beïnvloed?’ De Grieken hadden contact met Perzië, en zeker tijdens de periode van Alexander de Grote vond er een rijke uitwisseling aan ideeën plaats tussen Perzië en Griekenland, en tussen Perzië en de Hindoestaanse wereld aan de andere kant. Dat laatste bracht ook Griekse invloeden naar India en andersom. Daarnaast is de geschiedenis van de wiskunde, zoals alle geschiedenissen, gecompliceerd en genuanceerd. Ik zal in dit artikel niet te diep op deze details ingaan, maar een aantal wiskundige fenomenen benoemen waarvan vrij zeker is dat ze een groot deel van hun oorsprong buiten Europa hebben.
Leegte en dualiteit
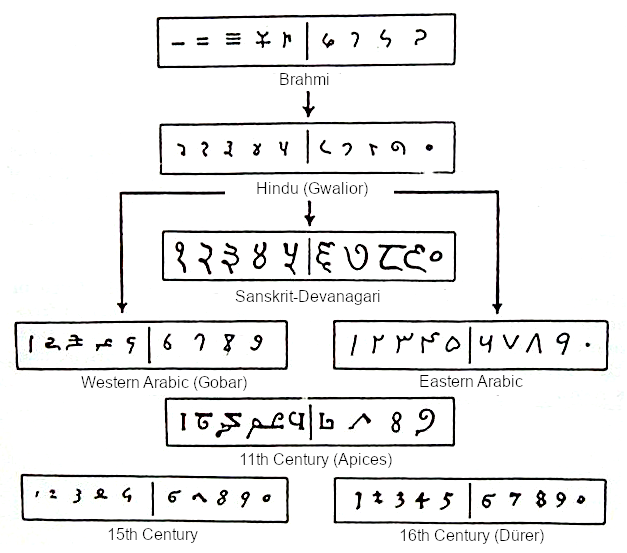
Laat ik beginnen met iets waar we praktisch constant gebruik van maken, elke keer dat we ook maar iets wiskunde- of rekengerelateerds doen: ons huidige, decimale getalsysteem. Dat vindt zijn oorsprong in India, en is naar Europa gekomen via het Midden-Oosten.
Een belangrijke toevoeging om notatie van getallen minder verwarrend te maken is het getal 0. Het Griekse en Romeinse getalsysteem kende geen 0. In veel geschriften werd wel een op plaatsing gebaseerd getalsysteem gebruikt, maar bijvoorbeeld in het Babylonische systeem (dat gebaseerd was op een hexadecimaal getallenstelsel) was het getal 30 slechts door middel van context te onderscheiden van ½. (In een decimaal systeem zou dit betekenen dat er geen verschil zou zijn in notatie tussen 5 en 0,5). Er werden wel symbolen gebruikt om binnen een getal aan te geven dat die plek ‘leeg’ was (zoals nodig is voor het getal 305) maar dit kan niet gezien worden als een werkelijke 0 omdat dit symbool niet opzichzelfstaand gebruikt werd. De Indiase dichter en wiskundige Pingala gebruikte voor het eerst het woord sunya, dat ‘leeg’ betekent, om te refereren naar het getal 0. Bekend is de tempel Chaturbhuj, gewijd aan de hindoegod Vishnu, waarin de oudste inscripties van het getal 0 zouden staan.
Nog obscuurder dan het getal 0 zijn de negatieve getallen. In Europa heeft het behoorlijk lang geduurd tot het concept van een negatief getal werd geaccepteerd. Hoewel men al langer algebraïsche vergelijkingen bestudeerde, waar men zeker negatieve oplossingen tegenkwam, werden zulke oplossingen standaard aangemerkt als ‘absurd’. Zelfs tot in de 18e eeuw werden negatieve oplossingen meestal simpelweg genegeerd. De Engelse wiskundige Francis Maseres zei in 1759 over de negatieve getallen: “[They] darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple.” Negatieve getallen worden echter al beschreven in het Chinese werk “The Nine Chapters on the Mathematical Art,” dat aan de fundamenten staat van de Chinese wiskunde en qua invloed wel wordt vergeleken met de Elementen van Euclides. De geschiedkundige Jean-Claude Martzloff heeft gesuggereerd dat de Chinezen het concept van negatieve getallen makkelijker zouden accepteren dan Europeanen omdat dualiteit een centrale rol heeft in de oud-Chinese filosofie. Doorgaand op die gedachte, kan gespeculeerd worden dat de hindoes het concept van een 0 makkelijker konden aanvaarden omdat sunyata, ‘leegte’ (hetzelfde woord dat gebruikt wordt om te refereren naar de 0), een centrale rol heeft in de boeddhistische filosofie.
Algebra
Een volgend soort rare getallen zijn de irrationale getallen. Beroemd is de legende van de Griek Hippasus die voor het eerst bewees dat √2 irrationaal is en daarvoor werd vermoord omdat dit niet strookte met het wereldbeeld van de Pythagoreeërs. Lang bleven de Grieken irrationale getallen beschouwen met argwaan, bijvoorbeeld door te stellen dat er een verschil was tussen ‘kwantiteiten’ die men gebruikt om lengtes mee te meten, en ‘getallen’ – √2 is een kwantiteit, geen getal. In het algemeen waren de Grieken erg gericht op geometrie: ze bewezen vooral geometrische stellingen met geometrische bewijzen. Met algebra, de tak van sport om een vergelijking op zichzelf staand op te schrijven en te manipuleren, waren ze niet echt bezig.
Het woord algebra komt van het Arabische al-Jabr en specifiek van de naam van het boek van een van de grootste namen in de geschiedenis van de algebra: de Pers Muḥammad ibn Mūsā al-Khwārizmī. Hij schreef het boek ‘The Compendious Book on Calculation by Completion and Balancing’ (al-Kitāb al-Mukhtaṣar fī Ḥisāb al-Jabr wal-Muqābalah), waarin voor het eerst systematische methodes voor het oplossen van lineaire en kwadratische vergelijkingen werden besproken, zoals kwadraatafsplitsen (‘completing the square’) en een term ‘naar de andere kant halen’, waarnaar ‘balancing’ refereert. Zijn nisba al-Khwārizmī, wat aanduidt dat hij afkomstig was uit Khwarazm, werd Algoritmi in het Latijn. Hier komt ons woord ‘algoritme’ vandaan. Dezelfde man schreef de werken On the Calculation with Hindu Numerals rond 825 and On the Use of the Hindu Numerals rond 830, die het hindoestaanse getalsysteem hebben gepopulariseerd in Perzië en daarna in Europa. Voor de islamitische wiskundigen werd het conceptuele verschil tussen ‘kwantiteiten’ en ‘getallen’ steeds minder belangrijk. Zij spraken van ‘uitspreekbare’ en ‘onuitspreekbare’ getallen – √2 was onuitspreekbaar (omdat er niet één woord voor was, maar het alleen met een zin beschreven kon worden zoals ‘de wortel van twee’) – maar beide typen getallen waren in elk geval getallen. Ook het decimale getalsysteem (kommagetallen) komt oorspronkelijk uit Arabië, en is daar ontwikkeld als extensie van de hindoestaanse manier om getallen te noteren.
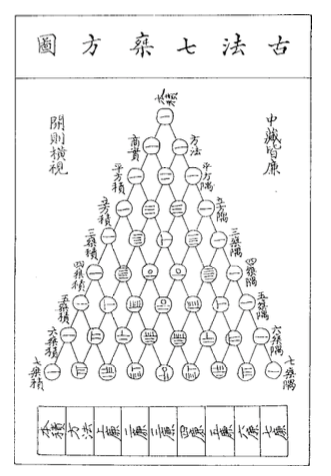
Chinese eliminatie
Het meest opzienbarende feit dat ik ben tegengekomen gekomen in mijn zoektocht naar de wortels van wiskunde heeft te maken met Gaussische eliminatie – de methode waarmee eerstejaars wiskundestudenten eindeloos matrices in ‘echelonvorm’ moeten brengen. Deze techniek dankt zijn naam aan de beroemde wiskundige Carl Friedrich Gauss, die leefde van 1777 tot 1855. In onze eerdergenoemde Nine Chapters is echter het volgende fragment te vinden.
“Now given 3 bundles of top grade paddy, 2 bundles of medium-grade paddy, [and] 1 bundle of low grade paddy. Yield: 39 dou of grain. 2 bundles of top grade paddy, 3 bundles of medium-grade paddy, [and] 1 bundle of low grade paddy, yield 34 dou. 1 bundle of top grade paddy, 2 bundles of medium-grade paddy, [and] 3 bundles of low grade paddy, yield 26 dou. Tell: how much paddy does one bundle of each grade yield?
Answer: Top grade paddy yields 9 14 dou [per bundle]; medium grade paddy 4 14 dou; [and] low grade paddy 2 34 dou.
The Array [Fangcheng] Rule
[Let Problem 1 serve as an example,] lay down in the right column 3 bundles of top grade paddy, 2 bundles of medium grade paddy, [and] 1 bundle of low grade paddy. Yield: 39 dou of grain. Similarly for the middle and left column.
Use [the number of bundles of] top grade paddy in the right column to multiply the middle column then merge. Again multiply the next [and] follow by pivoting. Then use the remainder of the medium grade paddy in the middle column to multiply the left column and pivot. The remainder of the low grade paddy in the left column is the divisor, the entry below is the dividend. The quotient is the yield of the low grade paddy . . .”
Wat hier beschreven wordt, is min of meer een matrix, die gebruikt wordt om een stel van drie lineaire vergelijkingen met drie onbekenden (top grade paddy, medium-grade paddy en low-grade paddy) op te lossen met een techniek die equivalent is aan Gaussische eliminatie.
Rijstvelden?
Het valt natuurlijk op dat dit probleem volledig in praktische termen (de kosten van verschillende kwaliteit rijst) geformuleerd is. Dit heeft geschiedkundigen er wel toe gebracht om te zeggen dat Chinese wiskunde (en ook islamitische of Babylonische, waarvoor hetzelfde geldt) ‘slechts’ praktisch georiënteerd was, en daarom niet echte zuivere wiskunde genoemd kan worden. We moeten echter oppassen om niet te snel zulke conclusies te trekken.
Een reden dat wordt gezegd dat niet-Griekse wiskunde ‘praktisch’ is, is dat veel andere volken niet zoals de Grieken gefocust waren op algemene stellingen en bewijzen. We zien ook in het Chinese werk dat er veel specifieke voorbeelden worden gegeven en dat bij de methodes om ze op te lossen wel uitgelegd wordt waarom die werken, maar niet inductief bewezen wordt dat het werkt. Dat laatste deden de Grieken wel, dat moeten we ze nageven. We kunnen ons echter afvragen of het feit dat in een wiskundig werk de vragen in zo’n praktische taal geformuleerd zijn, werkelijk betekent dat de schrijvers slechts geïnteresseerd waren in praktische problemen.
Liu, de belangrijkste commentator van dit Chinese werk, merkt op: “It is difficult to comprehend in mere words, so we simply use paddy to clarify.” Dit lijkt te suggereren dat het opschrijven van een vraagstuk in ‘mere words,’ dat wil zeggen in abstracte termen, zoals wij de neiging hebben om te verbinden aan ‘pure wiskunde’, hem niet zo zeer interesseerde –het verandert immers het probleem niet en het maakt het moeilijker om te noteren. Ook in Babylonische werken worden problemen in praktische taal geformuleerd, terwijl het problemen zijn waarvan moeilijk voorstelbaar is in welke praktische situatie ze zouden kunnen voorkomen. Bijvoorbeeld:
I have added up seven times the side of my square and eleven times the area.
In welke praktische situatie tel je de zijkant en de oppervlakte van een vierkant bij elkaar op? Is dit niet gewoon een kwadratische vergelijking?
We kunnen ons dus afvragen of het een kwestie van gebrek aan abstract begrip is, of meer een kwestie van notatie, dat in deze werken wordt gerefereerd naar muren en rijstvelden in plaats van x’jes en y’tjes.

Ter afsluiting
Als laatste heb ik nog twee grappige feitjes die ik ben tegengekomen terwijl ik onderzoek deed voor dit artikel, die ik graag nog wil delen. Als eerste een notatiekwestie. De Arabische wiskundige Al-Samaw’al al-Ba ̄hir fi-l-jabr (‘The Shining Treatise on Algebra’) schreef over negendegraads polynomen, waarbij hij tegen ongemakkelijke notatieproblemen aanliep. In de taal die tot zijn beschikking stond, werd x^9 beschreven als ‘cube cube cube’, 1/x als ‘part of thing’ en 1/x^9 als ‘part of cube cube cube’. Dit maakt de berekeningen er allemaal niet makkelijker op.
Het laatste voorbeeld van niet-Westerse wiskunde dat ik wil aanhalen komt uit een boek van de Chinees Qin Jiushao, die leefde in de 11e eeuw na Christus, getiteld Shushu Jiuzhang. In dit boek wordt een benaderingsmethode beschreven om de decimalen van een antwoord één voor één te vinden. Deze methode staat nu bekend als de Ruffini-Horner procedure. Ik denk dat er een passendere naam voor bestaat.
Geschiedenis van de natuurkunde: Alhazen, vader van de optica
Door Daan Hoogcarspel
De optica is een tak van de natuurkunde die zich bezighoudt met het gedrag van licht en historisch gezien ook met de werking van het zicht. De ontwikkeling van de optica is een proces dat zich heeft afgespeeld in alle uithoeken van de wereld en dat begon met de geometrische optica.

Het verhaal van de geometrische optica begint, zoals bijna alle geometrische praktijken, in het oude Griekenland bij Euclides. Net als zijn boek over meetkunde startte Euclides’ behandeling van de optica met een verzameling axioma’s, bijvoorbeeld dat zicht in rechte lijnen gaat en dat dingen kleiner lijken als ze verder weg staan. Euclides’ theorie was voornamelijk een wiskundige theorie van perspectief en ging niet in op hoe zicht fysisch werkte. Daarnaast ging Euclides uit van de emissietheorie van visie.
De emissietheorie is de theorie dat zicht werkt door stralen die het oog verlaten en daarna objecten raken die vervolgens zichtbaar zijn. Dit idee heeft wat weg van hoe ray tracing werkt binnen computergraphics. Deze (incorrecte) theorie over hoe zicht werkt, bleef lang in stand in de Griekse Oudheid en de Romeinse tijd daarna.
Ook Ptolemaeus, een invloedrijk Grieks wetenschapper, was een aanhanger van de emissietheorie. Wel droeg hij veel nieuws bij aan de optica. Zo zou hij tot het inzicht zijn gekomen dat bij spiegelen de hoek van inval even groot is als de hoek van terugkaatsing, en bedacht hij diverse andere theorieën die te maken hebben met breking van licht.
Hoewel al dit werk, en nog veel meer werk van andere geleerden uit de oudheid, erg belangrijk was voor de optica, vormt het nog niet echt de basis voor de moderne optica zoals we deze kennen. Hiervoor moeten we kijken buiten Europa, naar de Arabische wereld en het islamitische gouden tijdperk.
Het islamitische gouden tijdperk was een tijd tussen de achtste en veertiende eeuw (in onze jaartelling) waarin er grote culturele en economische bloei was in de Arabische wereld. In die periode zijn er veel ontwikkelingen geweest op het gebied van de wiskunde en de natuurwetenschappen. Op het gebied van de wiskunde werd bijvoorbeeld de algebra uitgevonden en de trigonometrie ontwikkeld.
Een van de belangrijkste figuren binnen de wetenschap in deze periode was Abu Ali al-Hasan ibn al-Haytham, die in het westen bekend staat als Alhazen. Hij leefde van 965 tot 1040 en wordt ook wel de vader van de moderne optica genoemd. Wat Alhazen kenmerkt in zijn manier van wetenschap doen is zijn nadruk op het bewijzen van al zijn uitspraken, iets wat we nu als vanzelfsprekend beschouwen wanneer we wetenschap bedrijven.

Een voorbeeld van deze wetenschappelijke methode is hoe Alhazen de emissietheorie van het zicht verwerpt en correct beredeneert dat licht wordt gevangen door de ogen. Als bewijs van deze hypothese komt Alhazen bijvoorbeeld met het feit dat het pijn doet om in de zon te kijken en dat licht daarom werkt op het oog in plaats van dat het oog zelf iets uitzendt. Ook voert hij het feit aan dat een fel licht een beeld kan achterlaten op het netvlies dat niet direct verdwijnt wanneer je wegkijkt. We zien dat Alhazen zijn stellingen bewijst door het verzamelen van data en hiermee foutieve theorieën verwerpt die eeuwenlang werden aangehangen.
Naast het verwerpen van de emissietheorie van het zicht heeft Alhazen ook onderzoek gedaan naar meer geometrische aspecten van de optica. Hij keek naar beelden geproduceerd door spiegels van verschillende vormen, bijvoorbeeld bollen en cilinders. Een probleem dat hij geometrisch oploste, is een wiskundig probleem over reflecties in bollen. Het probleem werd opgesteld door Ptolemaeus en wordt nu Alhazens probleem genoemd. Alhazens probleem vraagt welk punt op een bol een lichtstraal reflecteert van een gegeven lichtbron naar een waarnemer. Wiskundig komt dit neer op het oplossen van een vierdegraads vergelijking. Het probleem werd pas algebraïsch geformuleerd en opgelost in 1965 door Jack Elkin.
Alhazens theorie van de optica werd vertaald naar het Latijn en is van grote invloed geweest op de westerse theorieën van optica die volgden. Daarnaast heeft hij nog veel meer bijgedragen aan allerlei gebieden van de wetenschap. Alhazen was een ware wetenschapper die zijn hypotheses ondersteunde met empirisch bewijs en was daarmee zijn westerse collega’s decennia voor.