How black holes swap space and time

Afbeelding 1. Een zwart gat.Wat je ziet is alle materie die in het zwarte gat valt; het zwarte gat zelf is een klein bolletje in het midden van de afbeelding dat nauwelijks zichtbaar is. Maar wat gebeurt er als je écht het zwarte gat bereikt en over de rand valt? Afbeelding: ESO / L. Calçada.

Gravity is geometry

For the physics enthusiast today, the idea of space and time being one unit seems natural, but more than 100 years ago it was one of Albert Einstein’s greatest insights and gifts he left us. Another was that he realized that gravity, the force keeping us in bed every morning, was equivalent to the curvature of spacetime. In order to be able to describe what happens in curved spacetime, we need to understand a very important tool from mathematics: the metric g. The metric is a tool that encapsulates the geometry of space and time. More concretely, it unifies information about the lengths and angles between two basis vectors describing the spacetime. What does that mean?

If you wanted to meet somebody in our 4d world, you would agree on a location (in space) with coordinates x, y, z, and on a time t, which when combined give us the vector (t, x, y, z). For simplicity we now pretend our spatial world is one-dimensional and ignore y, z. Hence our vector is just (t, x) = (t, 0) + (0, x), where we call (t, 0) and (0, x) the basis vectors¹. Now, generally the metric is just a table of numbers like

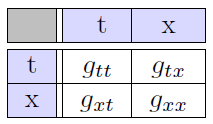
The numbers on the diagonal from top left to bottom right, which are labeled by g_tt and g_xx, describe the lengths of the basis vectors in the time direction (t, 0) and in the space direction (0, x) respectively. (Note that we can label any point in space (x,0) if we wish – for example, (x,0) measured in millimeters is quite different from (x,0) measured in metres! – so to actually describe the distance of (x,0) from the point (0,0) we need some further mathematical input. That input is precisely what the metric gives!) Likewise, the off-diagonal elements g_tx and g_xt describe the angles between the time and space basis vectors. If the basis vectors are perpendicular to one another then g_xt = 0, g_tx = 0 and hence we only consider the diagonal numbers.

One example, which describes our world without gravity is the Minkowski metric

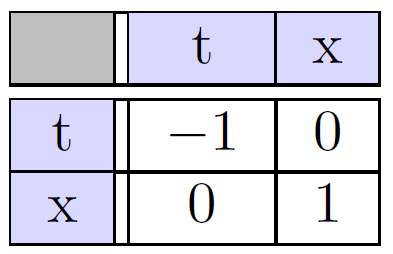
The fact that the component g_tt = −1 is crucial to understand why time and space, although being a unified concept, are still somewhat different conceptually. For instance, moving back and forth in a car just requires a shift in gears. But moving backwards and forwards in time is, at least to my knowledge, only possible if you are Tony Stark and want to defeat Thanos. Hence the defining property of time is that it forces us to move into one direction: the future and nothing else. The fact that time is so different from space can be encapsulated mathematically by a simple sign of -1 in the metric – quite surprising!

The black hole horizon

The Minkowski metric may still look simple, but that will change now, as we now have to turn to the case where we have gravity. The gold standard for describing gravity in the real world is the Schwarzschild metric. It describes how a spherical object, like the sun, with mass M, affects the curvature of spacetime in its surroundings. As we are dealing with spheres we may write r  for the outward coordinate instead of x. The table for the Schwarzschild metric looks as follows:

One might also wonder what the symbol r_s means. We call this the Schwarzschild radius and it takes the form

\( r_s = \frac{2GM}{c^2} \),

where we find Newton’s constant G, the speed of light c and the mass M, for the sun as an example. We see that as the mass M increases, the Schwarzschild radius also grows.

For the sun, the value of r_s is roughly three kilometers. That is, the sun itself is actually bigger than its Schwarzschild radius, and we cannot reach that particular distance. However, very compact objects also exist that are smaller than their own r_s. From analogies to Newton’s theory we can identify the Schwarzschild radius with the radius at which photons are no longer able to escape the gravitational force of an object with mass M. If no photons escape, meaning that no light escapes, an object will just look black from the outside. We just found a black hole! The Schwarzschild radius hence defines a horizon from which we cannot see any photons coming out. We call this the black hole horizon.

Swapping of time and space

What is now so special about the black hole horizon? Well at this point space and time change roles! You can see that this is true by looking at the Schwarzschild metric more closely. For that we first make it clear for ourselves that if we are outside the horizon (r > r_s) we find that

\( \left( 1 – \frac{r_s}{r} \right) > 0 \).

This means that as in the Minkowski metric the time component is negative (g_tt < 0) and the space component is positive (g_rr > 0), as expected.

Let’s imagine we jump into the black hole. As we pass through the horizon our radial distance r will become smaller than the Schwarzschild radius r_s. Now, like the photons above, no matter what we do or how fast we could go we cannot escape the gravitational pull of the black hole.

After this moment we will be at a point where r < r_s and hence

\( \left( 1 – \frac{r_s}{r} \right) < 0 \).

Now comes the crucial step. If we use this equation and put it into the Schwarzschild metric we will now find that the g_tt component is positive (g_tt > 0) and the g_rr component is negative (g_rr < 0), meaning that space and time, beyond the horizon, switched to time and space respectively!

Physical Intuition

So what happened here? How can it be that space and time change roles?

Let’s go back to the case of you falling into the black hole. After passing the horizon, due to the gravitational pull, you will continue to drift towards the singularity, i.e. the center of the black hole. For somebody outside the horizon, the singularity is some point in space. For you, however, the singularity is not a point in space, but a moment in time. You, and everything else inside the black hole, will eventually hit the singularity, no matter what you do and where you move. Remember that this is because not even light can escape a black hole.

To reiterate, the notion of hitting the singularity has two points of view:

• From the outside of the horizon it is a point in space and hence easy to bypass as we can just turn around.
• From the inside the singularity is a moment in time and hence impossible to avoid.

Gravity inside the horizon forces us to move towards our final destination: the singularity, which is now an event in time rather than a point in space. That is why around black holes, space and time change roles!

Recap

To summarize what have we learned:

• The metric g is a very important mathematical tool to understand the geometry of space and time and, as Einstein told us, it therefore also tells us something about gravity.
• We define time, as opposed to space, as the dimension where we can only go in one direction. The fact that time is special in that regard is related to the fact that the component² g_tt < 0.
• The Schwarzschild radius is the radius at which not even light can escape the gravitational pull. As a result, it defines the black hole horizon.
• After jumping into a black hole and passing the horizon, time and space change roles as now the singularity, i.e. center of the black hole, is no longer a point in space, but a moment in time.

To put it in a nutshell, black holes are cosmological entities with the ability to change space and time, making them truly the masters of the universe.

^[1] To be precise, these are not quite the basis vectors. The actual basis vectors are (1, 0) and (0, 1). Both basis vectors are scaled by the time t and location x respectively. But this detail will not affect the discussion that follows.

^[2] There is a small caveat to this statement. One could have also done the exact opposite and defined that time has a positive metric component and space a negative component. The important fact for the swapping of time and space is that the signs differ, and after passing the horizon the signs of these components change. For the curious, in the literature this mathematical freedom of overall sign choice is called the metric signature.