Kansloos in kansberekening

Het Monty Hall-probleem en onafhankelijke kansen

Van het laatste fenomeen dat ik in de inleiding noemde is een van de leukste voorbeelden het Monty Hall-probleem. Monty Hall was de gastheer van de Amerikaanse spelshow Let’s Make a Deal uit de jaren 60. In de show mag een deelnemer kiezen uit drie deuren. Achter een van die deuren zit een prijs, zoals een stapel geld, terwijl achter de andere twee deuren een geit staat, of iets anders waar de deelnemer waarschijnlijk niet op zit te wachten.

Het bijzondere element aan de show is dat, nadat je een deur hebt gekozen, deze nog niet open wordt gemaakt. Eerst gaat de gastheer, Monty Hall, een van de deuren die je niet hebt gekozen openmaken. Hij kiest hierbij  – in deze fictieve versie, in elk geval – altijd een deur waar de prijs niet achter zit, oftewel: hij kiest een deur waar een geit achter staat. Vervolgens geeft hij de deelnemer de optie: wil je de deur openen die je in eerste instantie hebt gekozen, of wil je graag wisselen naar de andere overgebleven deur? Deze hele situatie wordt geschetst in afbeelding 2.

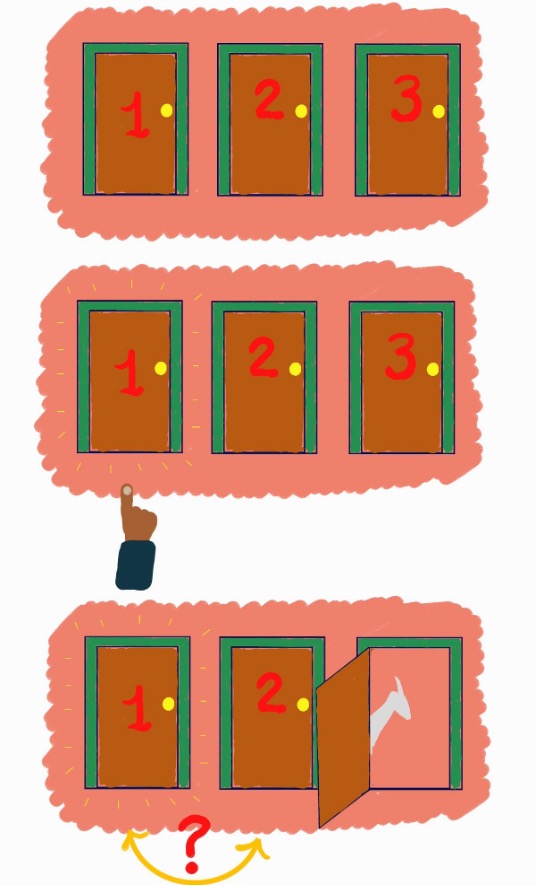
De vraag is nu: wat kunnen de deelnemers nu beter doen om hun winkans te vergroten? Denk er zelf maar eens over na. Houd je je eerste keus aan, of ga je wisselen? Het antwoord dat de meeste mensen in eerste instantie geven, is dat het niets uitmaakt. Achter een van de deuren zit immers de geit, en achter de andere de prijs. De kans is dus hoe dan ook 50 procent dat je de prijs wint. Toch?

Het juiste antwoord is echter dat je beter altijd kan wisselen! De kans dat je daarmee wint is twee op drie, dus ongeveer 67 procent. De reden hiervoor is dat Monty Hall altijd een deur kiest waar een geit achter staat. Hij gebruikt hiermee dus zijn kennis om de kansen te veranderen dat achter de overgebleven deuren een prijs zit, terwijl de kans op winst voor de deur die je in eerste instantie kiest niet is veranderd. Aangezien dit waarschijnlijk nog niet geheel overtuigend is, is het handig om dit stap voor stap uit te denken.

Aan het begin van het spel geven alle drie de deuren een kans van een derde om een prijs te winnen. Het spel kan vervolgens maar op twee verschillende manieren verlopen. Optie 1: Je hebt meteen de juiste deur gekozen, en achter jouw deur wacht een prijs. De kans dat dit gebeurt is een op de drie. In dit geval moet je om de prijs te winnen dus, nadat Monty achter een van de andere deuren een geit tevoorschijn heeft gehaald, bij jouw deur blijven en niet wisselen. Optie 2: Je hebt oorspronkelijk niet de juiste deur gekozen. Dit gebeurt in twee derde van de gevallen. Van de twee overgebleven deuren opent Monty de deur waar de geit achter staat, en de andere deur, de deur die jij niet hebt gekozen, leidt dus tot de prijs. In dit geval moet je dus wisselen van deur om de prijs te winnen. Zie ook afbeelding 3.

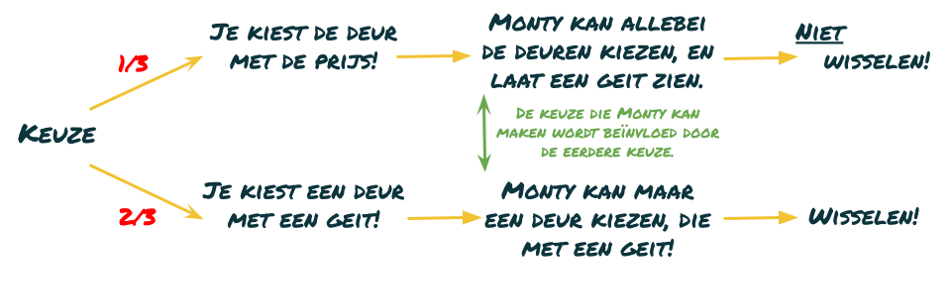
Samenvattend: in twee derde van de gevallen kan je dus beter wisselen, terwijl je maar in een derde van de gevallen beter bij je eerste keuze kan blijven. Als je dus niet weet wat je gekozen hebt, zoals tijdens het spel het geval is, kan je het beste altijd wisselen; dan win je twee op de drie keer een prijs.

Het leuke van dit probleem, is dat je ongetwijfeld bepaalde familieleden of vrienden hebt aan wie je het bovenstaande twintig keer kan uitleggen, inclusief tekeningen, tabellen en diagrammen, maar dat ze je nog steeds niet zullen geloven. Als je me niet gelooft dat er aan de bovenstaande rotsvaste redenering getwijfeld kan worden, probeer het dan voor de grap maar eens uit. Je zal zien dat deze uitkomst flink indruist tegen de intuïtie die veel van ons hebben.

Een vergelijkbare situatie waarin de intuïtie van deze mensen wél klopt, is die waarin Monty een van de deuren opent zonder te weten waar de prijs is. In dat geval zijn er drie verschillende situaties te onderscheiden met elk dezelfde kans: 1. Je kiest de goede deur, en Monty zal dus een deur met daarachter een geit openen. Dit gebeurt weer met een kans van een derde. 2. Je kiest een verkeerde deur, en Monty opent een deur met een geit. De kans dat dit gebeurt is weer een derde: twee derde kans dat jij een verkeerde deur kiest, en vervolgens vijftig procent kans dat Monty de geit-deur kiest. 3. Je kiest de verkeerde deur en Monty opent de deur met de prijs erachter. Ook hier is de kans weer één op drie. In dit geval verlies je dus, of je nou wisselt naar de overgebleven deur, of blijft bij je eerste keuze. Het maakt in deze situatie dus niet uit of je wisselt of niet; de kans dat je wint is sowieso een derde.

Vergelijkbaar gaat het wanneer Monty aan het begin van het spel een van de deuren opent, en je daarna een van de overgebleven deuren laat kiezen.

De laatste twee scenario’s hebben met elkaar gemeen dat de twee keuzes – die van jou en die van Monty – onafhankelijk van elkaar gebeuren, terwijl dat in het eerste scenario, het “echte” Monty Hall-probleem niet zo is. Als de deelnemer in dat scenario met zijn eerste keuze niet de deur met daarachter de prijs kiest, dan zit achter een van de overgebleven deuren namelijk de prijs, terwijl achter de andere de geit zit. Monty wordt dan dus gedwongen om die laatste deur te kiezen. Als jij echter wel de juiste deur hebt gekozen, kan Monty nog kiezen tussen de overgebleven deuren. De keuze die Monty kan maken wordt dus beïnvloed door de keuze van de deelnemer, en de twee keuzes zijn zodoende dus niet meer onafhankelijk. Ik heb dat ook aangegeven in groen in afbeelding 3.

Deze set-up voor de show is natuurlijk bewust gekozen, zodat deelnemers onterecht denken dat er geen statistisch voordeel is om ofwel bij je eerste keuze te blijven, of te wisselen. Als mensen dat geloven, blijkt dat ze meer geneigd zijn om bij hun eerste keuze te blijven. Dat komt door een andere eigenaardige psychologische trek die veel mensen hebben. We vinden het namelijk erger om iets te verliezen, dan we het leuk vinden om iets te krijgen. Mensen zien dan het scenario waarin ze voor de juiste deur hebben gekozen, maar toch wisselen, als een situatie waarin ze iets verloren hebben wat ze al hadden gewonnen. Deze angst iets te verliezen zorgt ervoor dat veel mensen het liefst bij hun eerste keuze blijven. Dit is een type van cognitieve vooringenomenheid die verliesaversie wordt genoemd. Meer voorbeelden hiervan, en van andere bekende cognitieve vooringenomenheden, kan je terugvinden in het boek ‘Ons feilbare denken’ van Nobelprijswinnaar Daniel Kahneman, wat ik niet genoeg kan aanbevelen.

Een ander interessant voorbeeld is de zogenaamde overleversvooringenomenheid. Die term refereert naar de logische denkfout die vaak optreedt wanneer men alleen naar een populatie kijkt die overblijft na een bepaalde selectie. Een bekende situatie waarin dit van belang was, is die van gevechtsvliegtuigen in de Tweede Wereldoorlog. Nadat deze vliegtuigen vol gaten van het slagveld terugkeerden, analyseerde de Amerikaanse statisticus Abraham Wald waar de meeste gaten in de teruggekeerde vliegtuigen zaten. Zie afbeelding 4 voor het resultaat. In plaats van te besluiten op die plaatsen de vliegtuigen te verstevigen, besloot hij dat de vliegtuigen juist overal waar géén gaten zaten verstevigd moesten worden. De reden is dat hij wist dat de vliegtuigen die terugkeerden en waarvan hij de kogelgaten zag zitten, de vliegtuigen waren die teruggekeerd waren. Die vliegtuigen konden dus blijkbaar doorvliegen, ondanks het feit dat ze daar beschoten waren. Juist daar waar geen gaten zaten waren vliegtuigen geraakt die niet meer terugkeerden, en daar moest dus versteviging aangebracht worden.

Grote getallen en toevalligheid

Om weer terug te keren naar kansrekenen: een andere situatie waarin we daar bijzonder slecht in zijn, is wanneer de kans op een bepaalde gebeurtenis misschien heel klein is, maar de mogelijkheid op die gebeurtenis heel vaak voorkomt. De kans dat die gebeurtenis dan ooit ergens plaatsvindt, kan dan toch aanzienlijk worden – soms wordt de gebeurtenis zelfs bijna onontkoombaar. Dit is het type gebeurtenis waar je iemand misschien hoort zeggen: ‘Dit kan geen toeval zijn!’, om vervolgens een achterliggende verklaring te zoeken, die wellicht complotachtige trekjes heeft.

Een leuk voorbeeld is dat iemand het nieuws van de volgende dag droomt.^[1] Laten we zeggen dat de kans dat dit gebeurt één op een miljoen is. Iemand die dit overkomt zal misschien wel denken dat hij of zij helderziend is, of een bovennatuurlijke ingeving heeft gekregen. In werkelijkheid is de kans dat dit op een gegeven dag voor iemand gebeurt, bijvoorbeeld alleen al in de stad Rotterdam ongeveer 50 procent.

Dat kan je als volgt zien. Als de kans op een gebeurtenis één op \( n\) is, maar een mogelijkheid op die gebeurtenis komt \( k \) keer voor, dan is de kans dat die gebeurtenis uiteindelijk plaatsvindt gegeven door de wiskundige uitdrukking

\( \text{kans} = 1- \left(1 – \frac{1}{n}\right)^k~.\)

De kans dat iets gebeurt is namelijk 1 min de kans dat het niet gebeurt, en als iets \( k \) maal niet moet gebeuren is de kans daarop de kans dat het één keer niet gebeurt tot de macht \( k \).

Een handige vuistregel die je hieruit kan halen, is dat de kans dat iets gebeurt meer dan 50% wordt als het aantal mogelijkheden dat die gebeurtenis plaatsvindt, \( k \), groter wordt dan \( 0{,}7n \). Vul maar eens \( k=0{,}7n \) in en plot de functie die ik hierboven beschreef als functie van \( n \), en je zal zien dat deze functie vrijwel onmiddellijk naar 0,5 gaat voor \( n \geq 4 \). In Rotterdam (ik heb de stad natuurlijk uitgezocht op het inwoneraantal) wonen ongeveer 700.000 mensen, dus als de kans één op een miljoen is dat een gegeven persoon het nieuws voorspelt met zijn droom, dan is de kans dat op een gegeven dag in Rotterdam iemand op deze wijze het nieuws voorspelt en zichzelf daarmee misschien een helderziende waant ongeveer 50 procent.

Meer algemeen kan je stellen dat de kans dat je in je leven iets overkomt, waarvan de kans één op een miljoen is dat dat gebeurt, ook ongeveer 50 procent is. Voor het gemak nemen we aan dat je gemiddeld gezien elk uur iets dergelijks kan overkomen, en aangezien de gemiddelde persoon een levensduur van ongeveer 700.000 uur heeft, komt dat dus met de bovenstaande vergelijking precies op 50 procent uit.

Een ander veel voorkomend voorbeeld is geraakt worden door bliksem. Het wereldrecord hiervoor is gezet door Roy Sullivan, een Amerikaanse boswachter. Hij is in zijn leven zeven keer door de bliksem geraakt! Wordt Sullivan gehaat door een of andere god, zoals Thor? Dat hoef je in ieder geval niet aan te nemen, want bliksem slaat op aarde zo’n 40 tot 50 keer per seconde in, en er lopen 8 miljard mensen rond die geraakt kunnen worden. Het is dus best te verwachten dat er na een aantal tientallen jaren tot een eeuw waarin cijfers worden bijgehouden, iemand blijkt te zijn geweest die zeven keer door bliksem is geraakt en dat heeft overleefd. Dit is zeker het geval als je kijkt naar personen die wonen en werken in een gebied met veel bergen en waar het warm en nat is, want daar komt bliksem veel vaker voor. Als de persoon ook nog eens buiten werkt, is de kans om door bliksem geraakt te worden natuurlijk nog veel groter.

Een laatste voorbeeld wat ik zelf leuk vind, is het voorspellen van de Amerikaanse verkiezingen. Elke vier jaar, wanneer het weer verkiezingstijd is in Amerika, komt er wel weer een nieuwsbericht langs over iemand die nu al tien keer op rij de uitslag van de verkiezingen correct voorspeld heeft op basis van zijn of haar zelf ontworpen model, en dat deze keer de voorspelling voor de een of de andere kandidaat is dat die zal winnen. Het leuke, of trieste, van de Amerikaanse verkiezingen, is dat er in grote lijnen maar twee uitkomsten zijn: de democraten winnen of de republikeinen winnen. Ook als je “model” simpelweg het opgooien van een muntje is, is de kans dat je in een gegeven verkiezingsjaar de correcte voorspelling levert dus 50 procent.

Wil je dat tien keer op rij, oftewel 40 jaar lang, goed doen, dan moet je muntje 10 keer juist vallen. De kans dat dat gebeurt is 1 op de \( 2^{10} = 1024 \). Er hoeven binnen de Verenigde Staten, met een bevolking van pakweg 350 miljoen mensen, dus slechts ongeveer 700 mensen al een tijd lang met een dergelijk model bezig te zijn voordat de kans groter dan 50 procent wordt dat je er een kan vinden die de afgelopen 40 jaar altijd goed zat. Het lijkt me niet onwaarschijnlijk dat dat aantal in realiteit veel hoger ligt, en dus spreekt het verschijnen van iemand die de verkiezingen met een model gedurende lange tijd correct voorspelt niet zozeer tot de kwaliteiten van dat model, maar meer tot het feit dat de Amerikaanse verkiezingsuitkomst maar twee echt mogelijke uitkomsten heeft, en het feit dat er veel mensen zijn die het interessant vinden om de verkiezingsuitslag te voorspellen.

Willekeur

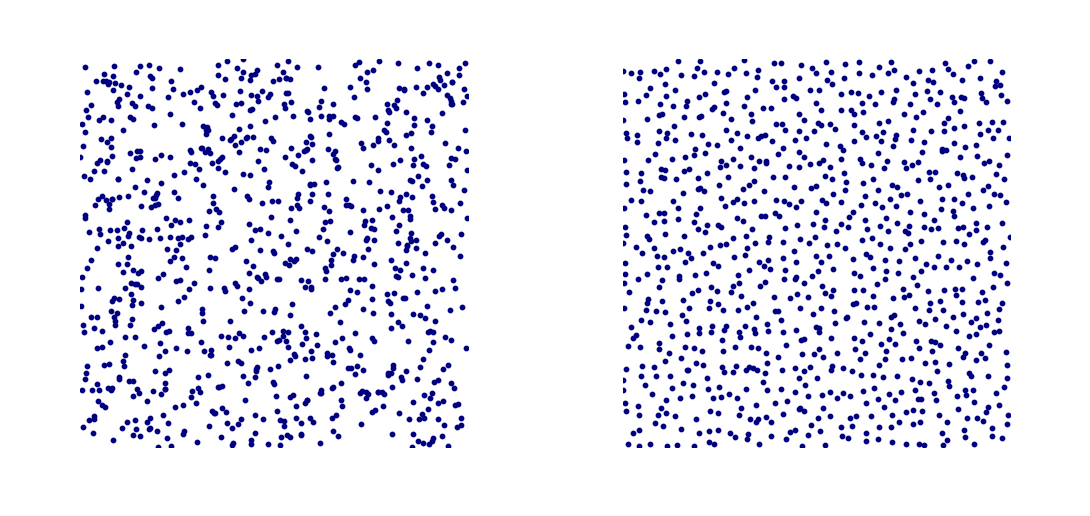
Ten slotte blijkt dat mensen vaak een volkomen onjuist beeld hebben van willekeur. Zo denken we vaak patronen te zien in dingen die in werkelijkheid willekeurig zijn, en andersom denken we vaak dat geordende dingen juist willekeurig zijn. Kijk bijvoorbeeld eens naar afbeelding 5. Is de linker of de rechter afbeelding een voorbeeld van een willekeurig verdeelde set puntjes? Het juiste antwoord is: de linker afbeelding. Toch kiezen de meeste mensen voor de rechter afbeelding. In de linker afbeelding zie je immers dat op veel plekken een aantal puntjes heel dicht bij elkaar liggen. Dit voelt voor veel mensen niet echt als willekeurig – het is alsof die puntjes graag dicht bij elkaar liggen.

Een vergelijkbare verwarring deed zich voor toen het programma iTunes werd uitgebracht^[2]. Het muziekprogramma beschikte in het bijzonder over een shuffle-functie. Toen die net uitkwam kreeg Apple veel klachten daarover. De shuffle zou namelijk niet willekeurig genoeg zijn. Klanten kregen vaak nummers na elkaar te horen die van hetzelfde type muziek waren, of van hetzelfde album, ook al hadden ze allerlei muziek door elkaar op een playlist gezet. Zoals ik hieronder zal uitleggen is dit juist een eigenschap die we kunnen verwachten van willekeurige distributies, hoewel we dat intuïtief dus niet zo ervaren. Uiteindelijk besloot Apple de shuffle-functie aan te passen, zodat vermeden werd om hetzelfde type nummer achter elkaar af te spelen. De nieuwe shuffle-functie, waarbij dus juist een mate van orde was aangebracht, ervoer de gebruiker wel als willekeurig.

Het fenomeen dat hier plaatsvindt noemen we clusteren, en het is zoals gezegd een eigenschap die je juist verwacht in willekeurige distributies. Neem bijvoorbeeld weer het voorbeeld van blikseminslagen.^[3] Stel dat er in een bepaald gebied gemiddeld eens per 33 dagen een blikseminslag is. We nemen hierbij aan dat de blikseminslagen volkomen onafhankelijk van elkaar en willekeurig gebeuren. Stel nu dat er op een dag, zeg maandag, een blikseminslag plaatsvindt. (Het zouden er zelfs meerdere kunnen zijn, natuurlijk – maar hoe dan ook: op maandag is de bliksem dus ingeslagen, en die dag is nu voorbij.) Op welke dag is de kans het grootst dat de volgende blikseminslag plaatsvindt? Het antwoord dat de meeste mensen geven, en wat ook precies de foute gedachtegang die meer algemeen plaatsvindt illustreert, is dat elke dag dezelfde kans op een inslag heeft, namelijk \(\frac{1}{33}\), of ongeveer 0,03. Het werkelijke antwoord is echter dat de kans op de volgende dag, namelijk dinsdag, het grootst is! De kans daarop is wel 0,03, zoals je zou verwachten, maar de kans dat de volgende blikseminslag op woensdag plaatsvindt is kleiner. Daarvoor moet namelijk eerst de bliksem niet inslaan op dinsdag, anders zou dinsdag de volgende dag zijn waarop bliksem inslaat. De kans op het niet inslaan op dinsdag en wél op woensdag is dus \( 0{,}97 \cdot 0{,}03 \). Voor donderdag geldt iets soortgelijks: als de bliksem dan voor het eerst weer inslaat  moet de bliksem eerst niet op dinsdag en woensdag zijn ingeslagen, en de kans dat dit allemaal gebeurt is dus \((0{,}97)^2 \cdot 0{,}03\). In het algemeen wordt de kans dat na \( n \) dagen de eerstvolgende blikseminslag plaatsvindt dus \( (0{,}97)^n \cdot 0{,}03 \). Die uitdrukking beschrijft een exponentiële demping van de kans dat de eerstvolgende inslag later en later zal vallen.

Een gerelateerde kansverdeling die hieruit voortkomt beschrijft de kans dat een bepaalde gebeurtenis een bepaald aantal keer \( k \) in een bepaald tijdsinterval plaatsvindt. De verdeling hangt af van het gemiddelde aantal keer dat die gebeurtenis plaatsvindt in dat tijdsinterval \( \lambda \), en heet een Poissonverdeling. De formule ervoor is

\( P(x=k) = \frac{\lambda^k e^{-\lambda}}{k!}~. \)

Zie ook afbeelding 6, waar deze kansverdeling voor een aantal verschillende waarden van \( \lambda \) is afgebeeld.^[4]

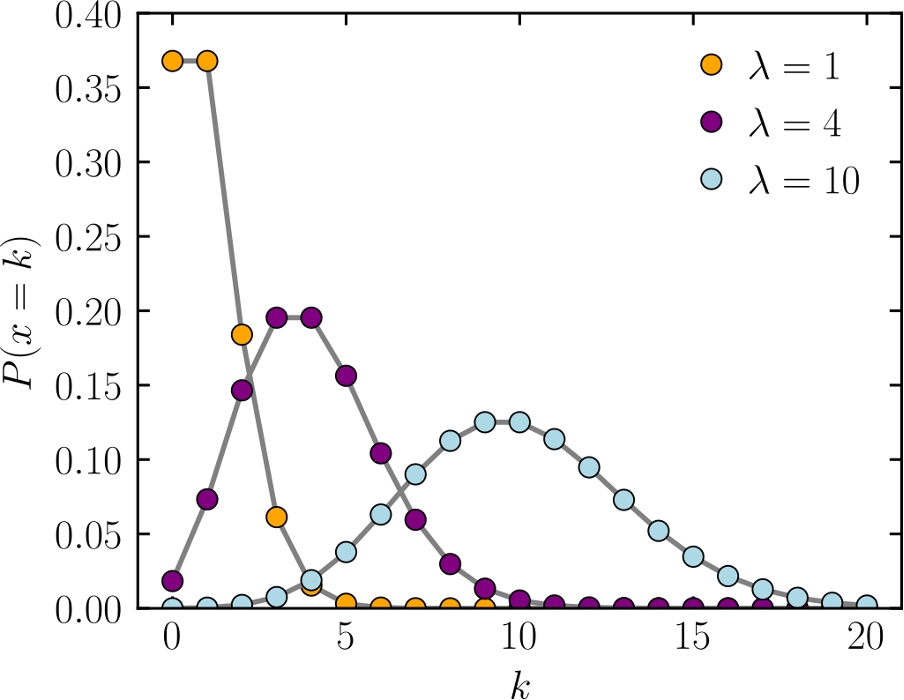
De Poissonverdeling beschrijft dus de kans dat een gebeurtenis een bepaald aantal keer voorkomt in een tijdsinterval, gegeven dat die gebeurtenis een constante gemiddelde kans heeft om te gebeuren, en dat de gebeurtenissen onafhankelijk van elkaar zijn. Zo beschrijft de verdeling dus ook de kans dat je tijdens het opgooien van een serie muntjes een gegeven aantal keer achter elkaar kop of munt gooit. De kans dat een lange aaneenschakeling van dezelfde uitkomst zich voordoet in een serie van worpen, wordt steeds groter naarmate die serie worpen langer en langer wordt, zodat je voor een grote dataset dus verwacht dat er hier en daar clusters optreden. Deze clusters zien mensen dan vaak als een reden om aan te nemen dat er iets in het spel is wat niet werkelijk willekeurig is. Van willekeurigheid verwacht je dus echter juist de aanwezigheid van die clusters. Als je de aanwezigheid van clusters in het geheel wil voorkomen, zeg in een set van muntworpen, dan krijg je een serie uitkomsten die eruitzien zoals KMKMKMKMKM, waar K kop aanduidt, en M munt. Dit volgt juist duidelijk een ordelijk patroon en is niet willekeurig. Hoe onnatuurlijk clustering ook lijkt; als je goed om je heen kijkt, zal je zien dat het in heel veel situaties voorkomt, bij allerlei zaken die (bij benadering) worden beschreven door Poissonverdelingen.

Zo zie je maar weer wat voor tegenintuïtieve verschijnselen je op dagelijkse basis kan tegenkomen, en hoe je daar met een klein beetje eenvoudige wiskunde orde in kan scheppen, en zo zin van onzin kan scheiden.

[1] Zie ook het artikel van New Scientist, waar ik dit voorbeeld van heb overgenomen, net als de later genoemde vuistregel van k = 0,7n.

[2] Over dit voorbeeld kwam ik te weten door dit YouTubefilmpje van het kanaal Vsauce.

[3] Dit illustratieve voorbeeld ken ik uit het boek The Better Angels of Our Nature van Steven Pinker.

[4] Je vraagt je misschien af of dit artikel nog wat met natuurkunde te maken heeft, maar ik zag exact deze afbeelding gisteren nog op een slide staan van een praatje bij een conferentie over quantumzwaartekracht!