
Wat is thermodynamica?
De natuur kent de fundamentele krachten die elk hun eigen domein hebben. De thermodynamica is echter veel meer overkoepelend. Ik zie thermodynamica graag als een theorie die je vertelt wat mogelijk is, ongeacht het precieze microscopische model dat je kiest. Ik denk bovendien dat je, als je een theorie ontwikkelt die in strijd is met de tweede hoofdwet van thermodynamica, met waanzinnig sterke argumenten moet komen om natuurkundigen te overtuigen. Thermodynamica is een hoeksteen van de moderne natuurkunde, dus het loont om die theorie zo goed mogelijk te begrijpen.
Tot op de dag van vandaag is de thermodynamica een actief onderzoeksgebied. De theorie die ooit begon als beschrijving van stoommachines en andere voorwerpen uit ons dagelijks leven, houdt fysici vandaag de dag vooral op niet-alledaagse schalen bezig – die van de astronomie of juist de quantumschaal. Op astronomische schalen lijkt thermodynamica iets te zeggen over quantumzwaartekracht – zie de artikelen zwaartekracht en entropie of zwarte gaten en thermodynamica.
In dit artikel neem ik je mee door een publicatie van Elliott Lieb en Jakob Yngvason, die de tweede hoofdwet van de klassieke thermodynamica graag preciezer wilden formuleren door deze te baseren op een stel axioma’s. Axioma’s, vooral bekend uit de wiskunde, zijn de uitgangspunten van een theorie: stellingen die je voor waar aanneemt en verder gebruikt om je theorie mee op te bouwen. Wat ik mooi vind aan de axioma’s van Lieb en Yngvason, is dat ze precies duidelijk maken wanneer de tweede wet geldig is en heel intuïtief maken hoe die werkt. Daarnaast is hun werk ook gemotiveerd door een groot openstaand probleem, dat ik in de laatste alinea kort toelicht.
De axioma’s
Ik val gelijk met de deur in huis, dan hebben we het moeilijkste gehad. In de rest van dit artikel leg ik uit wat deze hiërogliefen betekenen, dus je hoeft het uiteraard niet meteen te begrijpen. De twee auteurs voeren zes axioma’s in:
- Reflexiviteit: \(X\sim X\)
- Transitiviteit: \(X\prec Y\) en \(Y\prec Z\) impliceert dat \( X\prec Z\)
- Consistentie: \(X\prec X’\) en \(Y\prec Y’\) impliceert dat \((X,Y)\prec (X’,Y’)\)
- Schaalvrij: Als \(X\prec Y\) dan \(tX\prec tY\) voor elk positief getal \(t\)
- Splitsen en Combineren: \(X\sim(tX,(1-t)X)\) met \(t\) tussen \(0\) en \(1\)
- Stabiliteit: Als \((X,\epsilon Z_0)\prec (Y,\epsilon Z_1)\) met \(\epsilon\) kleiner dan een grenswaarde, dan \(X\prec Y\)
Bonus: Vergelijkingshypothese \(X\prec Y\) of \( Y\prec X\)
Op dit moment is het bovenstaande hoogstwaarschijnlijk nog abracadabra voor je, dus laten we gaan kijken wat de axioma’s nu precies zeggen!
Dit gaan we doen aan de hand van afbeeldingen 1 en 2. Voordat we dat doen, leg ik in de volgende alinea de notatie uit.

Wat betekent die notatie? (Ordeningsrelatie)
Wanneer ik noteer \(X\prec Y\) (lees dit als: “\(X\) gaat voor \(Y\)”), dan bedoel ik dat er een proces bestaat dat een toestand \(X\) verandert in een toestand \(Y\). Bijvoorbeeld: \(X=\text{roomijs}\) en \(Y=\text{suikerige melk}\). Kan je een proces verzinnen dat \(X\) in \(Y\) verandert? Ik weet er wel eentje: vergeten dat je ijs aan het ontdooien bent voor na het avondeten. Andersom bestaat er ook een proces, namelijk: zet je suikerige melk de volgende ochtend weer in je vriezer, of beter nog: gebruik je een ijsmachine, dan geldt hopelijk dat \(Y\prec X\). In dit geval bestaan er dus manieren om van \(X\) naar \(Y\) te gaan en terug; dit noteren we als \(\sim\):
\( X\prec Y\text{ en } Y\prec X\qquad\text{betekent ook wel}\qquad X\sim Y. \)
Verder kan ik ook nadenken over meerdere systemen tegelijkertijd: dan noteer ik de \(n\) toestanden als \((X_1,X_2,…,X_n)\) (denk bijvoorbeeld aan twee bakjes \((X_1,X_2)\) van een liter roomijs). Als laatste noteren we een veelvoud van een toestand \(X\) als \(tX\): \(3X\) staat in ons voorbeeld bijvoorbeeld voor drie liter roomijs en \(0{,}5X\) voor een halve liter.
Het verband met de tweede wet. Uit de axioma’s leiden Lieb en Yngvason (onder meer) af dat de mogelijkheid om van toestand \(X\) naar \(Y\) te gaan equivalent is aan het feit dat de entropie \( S(X)\) niet kan afnemen:
\( X\prec Y\qquad\iff\qquad S(X)\leq S(Y) \)
(Frederic Schuller legt het equivalentieteken \(\iff\) in zijn eerste college op youtube in meer detail uit). Hier staat eigenlijk precies de tweede wet van thermodynamica: tijdens een proces \(X\text{ naar }Y\) kan de entropie \(S\) nooit afnemen. Als je de bovenstaande zes axioma’s en de vergelijkingshypothese dus begrijpt, dan snap je wanneer de tweede wet van toepassing is. Aan de andere kant: mochten één of meer van de axioma’s niet gelden, dan is het onduidelijk of de tweede wet nog geldt.
Een middagje kleien
Laten we in het thema van de feestdagen wat cadeautjes maken. We beginnen met een groen balletje klei en de eerste drie axioma’s (zie afbeelding1). Door niets met het balletje te doen, heb ik nog steeds een bolletje klei: reflexiviteit. Hoe zal ik de cadeaudoos maken? Als ik een staaf plat druk op tafel, krijg ik een platte schijf. Daar past wel een op schaal gemaakt cadeautje in, toch? Dan moet ik wel eerst mijn bolletje staafvormig rollen. Omdat ik van het bolletje een staaf kan maken en van de staaf een platte schijf, kan ik dus van mijn bolletje een platte schijf maken: transitiviteit. Nu nog een strik er op; die maak ik uit rode klei. Het is heel logisch dat, als ik individueel uit groene respectievelijk rode klei een schijf respectievelijk een strik kan maken, ik ook van de twee samen een schijf én een strik kan maken: consistentie. Zonder consistentie, zou bijvoorbeeld de aanwezigheid van de rode klei kunnen impliceren dat ik niet meer de platte schijf kan maken. Dat is heel gek toch?
Goed, dan hebben we al de eerste drie axioma’s gehad – dat ging eigenlijk best snel!
Op naar de laatste drie axioma’s in afbeelding 2. Laten we nog een cadeautje maken, maar nu wat kleiner. Door met wat minder materiaal dezelfde stappen te ondernemen, kan ik natuurlijk een kleiner cadeautje maken: het proces is schaalvrij. Dit is mogelijk gemaakt door aan het begin wat klei apart te leggen van de rest. Andersom: wanneer ik klaar ben, kan ik ook weer de klei samenvoegen: splitsen. Bij het maken van een derde (en laatste) cadeautje in een blauwe kleur, is er per ongeluk een piepklein rood kleirestje meegekomen. Met dat piepkleine rode stukje erbij kan ik niet opeens meer maken dan ik al kon met mijn blauwe klei: stabiliteit.
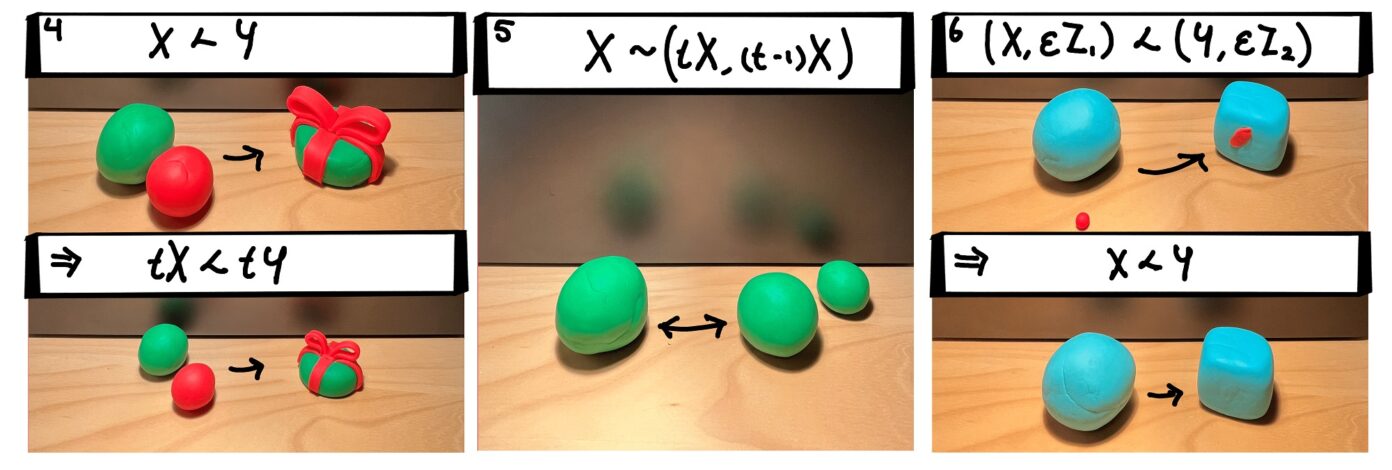
Dat waren de axioma’s alweer. Tot slot is er de vergelijkingshypothese, die vereist dat er een proces bestaat dat de ene toestand naar de andere brengt, eventueel in beide richtingen. Voor vormpjes van een vaste hoeveelheid klei is deze eigenschap vanzelfsprekend aanwezig in beide richtingen. Voor alle toestanden \(X\), \(Y\) van die klei, is het (volgens de afgesproken notatie) dus zo dat \(X\sim Y\).
Systemen waarbij voor alle toestanden \(X\) en, \(Y\) geldt dat \(X\sim Y\) zijn speciaal omdat de entropie voor zulke systemen voor alle toestanden dezelfde waarde heeft; de redenatie hiervoor volgt uit een simpele tekening zoals in afbeelding 3. In de “bonus”-alinea kom ik nog terug op een ander voorbeeld van zo’n systeem.
Voor andere processen, zoals bijvoorbeeld het maken van een tomatensoep, is het minder duidelijk of \(X\sim Y\) geldt. In hoeverre kun je nog terugkeren naar een tomaat (\( X \)) nadat deze tot soep (\(Y\)) is gemaakt?
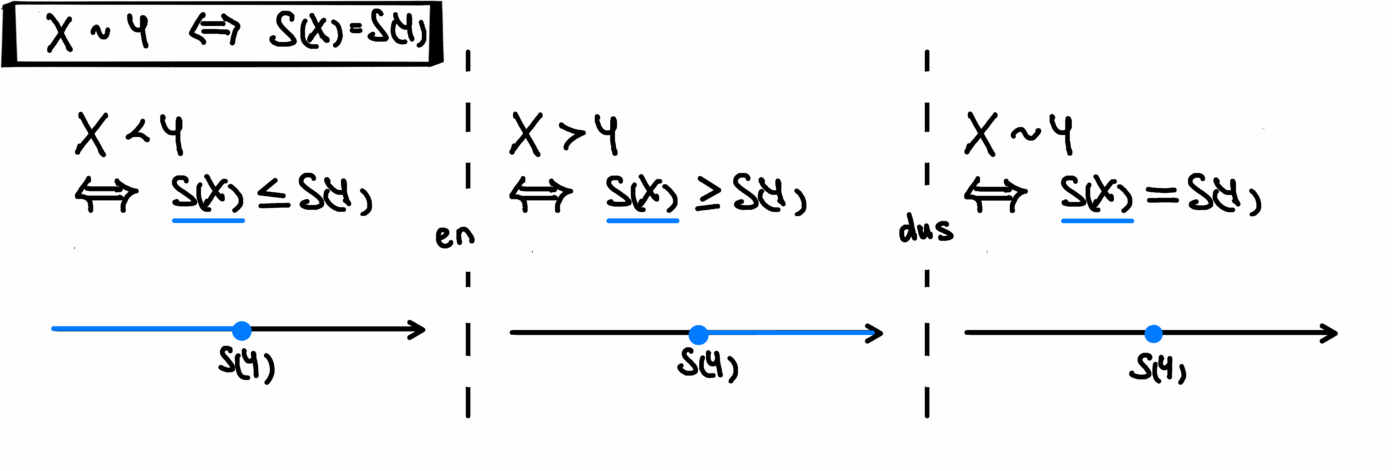
Een kleine kanttekening: niet te groot, niet te klein, adiabatisch én equilibrium
Mocht je nu denken dat je een proces hebt gevonden dat niet wordt gedekt door de zes axioma’s, dan zijn er toch nog wat haken en ogen: de betrokken fysische systemen mogen niet te groot of te klein zijn. Hoe klein? Hoe groot? Dat kan ik je helaas op dit moment niet precies vertellen, maar ik zal het hieronder wat verder toelichten. Ook moet het proces aan twee strikte eisen voldoen; die noemen we adiabatisch en equilibrium. Hieronder licht ik ook dit kort toe.
Niet te groot: Op grote schaal (denk bijvoorbeeld aan sterrenstelsels) werkt thermodynamica net iets anders. Om dit toe te lichten kan ik het beste refereren aan zogeheten intensieve en extensieve grootheden. Extensieve grootheden (bijvoorbeeld energie, massa) zijn afhankelijk van hoe groot je systeem is; intensieve grootheden (dichtheid, druk) zijn dat niet. Neem nu bijvoorbeeld temperatuur. In alledaagse begrippen is temperatuur een intrinsieke grootheid (de helft van een kop koffie heeft dezelfde temperatuur als de hele kop). In tegenstelling daarmee schaalt de interne temperatuur \(T\) van bijvoorbeeld een ster zoals de onze (een ster uit de zogeheten hoofdreeks) met de massa: \(T\propto M\). Voor zulke objecten is de temperatuur dus niet meer intensief, en het is niet onmiddellijk duidelijk dat voor heel grote sterren (of sterfusie) de wetten van de thermodynamica nog kloppen. Toch konden Lieb en Yngvason een entropiefunctie (van iets andere aard) definiëren. We hebben al eens eerder geschreven over thermodynamica op deze grotere schaal: zie klopt de tweede wet wel?
Niet te klein: Lieb en Yngvason houden zich nu bezig met de klassieke thermodynamica. Dan spreek je over de hierboven genoemde grootheden, onder andere temperatuur en druk. Zijn die concepten goed gedefinieerd voor één of een paar deeltjes? Nee! Vaak wordt temperatuur voorgesteld als het botsen en (intern) trillen van moleculen (zie ook afbeelding 3 in dit artikel). Pas wanneer je veel deeltjes bij elkaar hebt, ontstaat het collectieve gedrag waarbij we van temperatuur kunnen spreken. Voor druk geldt eenzelfde soort inconsistentie. In andere woorden: temperatuur en druk zijn emergente fenomenen. Laat het overigens ook duidelijk zijn dat ons vijfde axioma splitsen en recombineren niet mogelijk is met een enkel atoom. Hetzelfde geldt voor onder andere een energiepakketje: de gequantiseerde aard beperkt hierin.
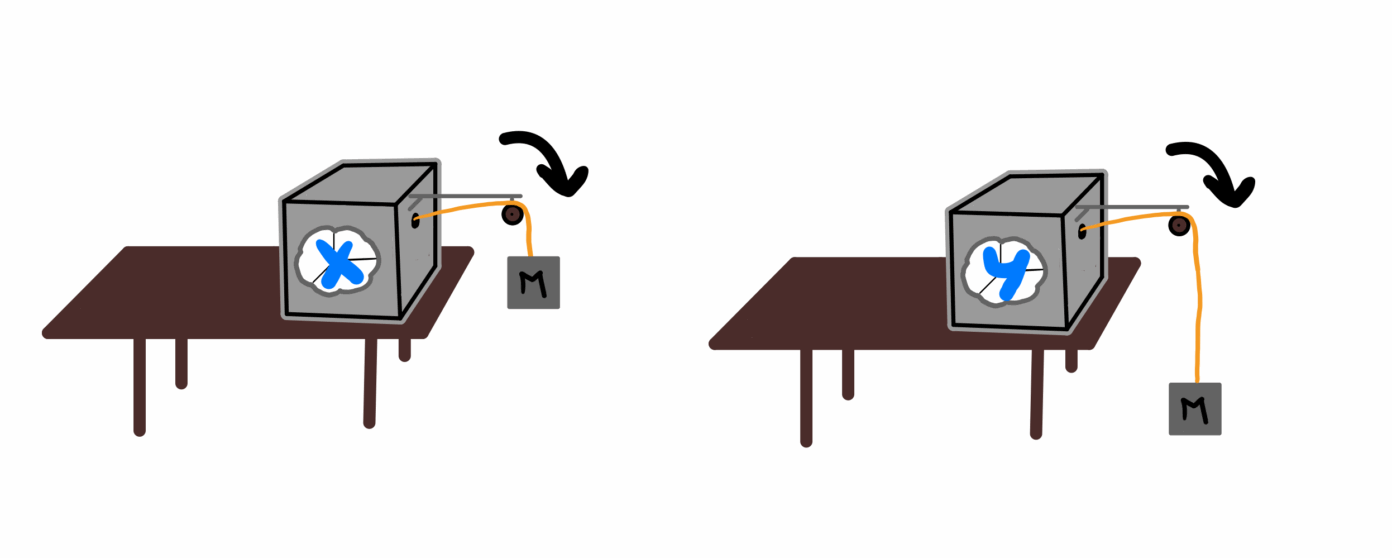
Adiabatisch en equilibrium: Het definiëren van de eigenschap adiabatisch moest voorzichtig gebeuren om het doel van Lieb en Yngvason te bewerkstelligen: ze stellen de volgende definitie voor (geïnspireerd door eerder werk van Max Planck): een proces is adiabatisch wanneer het mogelijk is om het te bewerkstelligen door een massa aan een touwtje, waarbij de massa na afloop van het proces arbeid heeft verricht door zich van positie te verplaatsen. Een apparaat (bestaande uit mechanische of elektrische onderdelen) mag hierbij helpen, zolang dat apparaat zich aan het einde van het proces weer in dezelfde toestand bevindt als ervoor (zie afbeelding 4).
De toestand voor en na het adiabatische proces mag ook niet zonder invloed van buitenaf uit zichzelf veranderen: dat noemen we equilibrium, oftewel: evenwicht.
Toch iets gevonden? Denk je toch een proces te kunnen vinden dat niet aan de axioma’s voldoet? Dan heb je meteen een leuk gespreksonderwerp voor het volgende avondje met vrienden 😉 De kans dat je gelijk hebt is natuurlijk niet zo groot, maar het is soms wel een leuke puzzel om te zien waaróm niet.
Was ons begrip van de tweede wet niet genoeg?
Door de jaren heen zijn er telkens opnieuw pogingen gedaan om de klassieke thermodynamica preciezer te formuleren. De bekendere klassieke formuleringen zijn afkomstig van Rudolf Clausius, vervolgens van Lord Kelvin en Max Planck, en later van Constantin Carathéodory. Elk van die formuleringen heeft een incrementeel stukje extra kennis over de natuur bijgebracht – en zo ook het werk van Lieb en Yngvason. Het is terecht dat men veel zorg besteedt aan een precieze formulering van een wet die zoveel gravitas draagt als de tweede hoofdwet. Op welk begrip hebben ze de nadruk gelegd?
Lieb en Yngvason merken op dat de thermodynamica, zoals die nu onderwezen (en bij strekking begrepen) wordt, zich onder andere baseert op empirische ondervindingen en intuïtie. Wanneer we het dan bijvoorbeeld in tekstboeken hebben over ‘hitte’, ‘warm’ en ‘koud’ vragen ze zich af wat de precieze vertaalslag is naar de wiskunde; ze willen van thermodynamica een ‘ideale fysische theorie’ maken: een theorie waarbij de vertaalslag naar pen en papier duidelijk is en er na de vertaling niet per se meer vertrouwd hoeft te worden op intuïtie. Daarnaast hadden ze een aantal specifieke en genuanceerde vragen; die kun je terugvinden in de inleiding (secties 1A en 1B) van het artikel. Eén sprong daar voor mij bovenuit: bijna alle tekstboeken baseren de klassieke thermodynamica op de differentieerbaarheid van functies. Toch zijn er fysisch relevante functies die niet differentieerbaar zijn. Dit komt al voor bij een alledaags verschijnsel zoals water koken (faseovergangen).
Hoewel de tweede wet al lang experimenteel geverifieerd is, ook in zulke gevallen, kan je je natuurlijk afvragen wat dan wel de onderliggende wiskundige structuur moet zijn die de tweede wet motiveert. Indien je die structuur hebt gevonden, kan je de vertaalslag maken en de ‘wiskundige molen’ aanzetten: wellicht vind je dan wel een experimenteel voorstel waar men eerst helemaal niet aan kon denken omdat we nog in termen van ‘differentieerbaar’ dachten. Dat vind ik het meest spannend aan overwegingen zoals deze, alhoewel ik de kans nog steeds klein acht dat we een nieuw experiment vinden om klassieke thermodynamica beter te begrijpen.
Over spannend gesproken: ik denk dat de precieze formulering nog het best is gemotiveerd door het open probleem dat ik had beloofd te noemen. Dit brengt me bij mijn laatste alinea.
Bonus: quantummechanica is net als klei
Quantumtoestanden zijn even vervormbaar als de klei. In haar fundament kun je de quantummechanica namelijk als een zogeheten unitaire theorie beschouwen. Dat betekent dat voor elke transformatie van een quantumtoestand \(X\) naar \(Y\) ook de terugtransformatie \(Y\text{ naar } X\) mogelijk is (dus \(X\sim Y\) voor alle quantumtoestanden). Net zoals het geval was bij de klei, dus! Met andere woorden: elke quantummechanische toestand heeft vanuit dit axiomatische perspectief dezelfde entropie (zie ook weer afbeelding 3).
Dit is wellicht problematisch voor onze alledaagse ervaring: als je aanneemt dat de unitariteit van quantummechanica ook aanwezig is op menselijke of zelfs astronomische schaal, dan is de tweede wet weliswaar waar, maar niet heel veelzeggend: alle toestanden hebben dezelfde entropie, dus entropie neemt inderdaad nooit af.
De oplettende lezer zou mij nu, terecht, kunnen wijzen op een fout: ‘had je niet eerder gezegd dat de axioma’s niet van toepassing zijn op een klein systeem?’ Inderdaad, eigenlijk had ik de statistische fysica moeten aanhalen. Toch blijft het waar dat quantummechanica unitair is en de entropie niet verandert (zie bijvoorbeeld de stelling van Liouville)1. Begrijpen hoe de tweede hoofdwet (en specifiek, onomkeerbaarheid) volgt vanuit de fundamentele principes van quantummechanica, is dan ook een grote open vraag. Lieb en Yngvason formuleren het als volgt:
If the law of entropy increase is ever going to be derived from statistical mechanics—a goal that has so far eluded the deepest thinkers—then it is important to be absolutely clear about what it is that one wants to derive.
Afsluitend
Zelf kan ik mijn enthousiasme nauwelijks bedwingen als ik lees over grote openstaande problemen, en ik neem aan dat hetzelfde geldt voor jou als lezer als je mijn artikel hebt uitgelezen. Indien je nieuwsgierig bent geworden naar de afleiding van Lieb en Yngvason, heb ik hun werk hieronder gelinkt. Als je de introductie leest, vertellen Lieb en Yngvason hoe je de vergelijkingshypothese nog kunt vervangen door drie axioma’s en dat er nog verdere overwegingen gemaakt worden om de thermodynamica in totaal op vijftien axioma’s te baseren. Daarover vertel ik een andere keer graag nog wat meer – tot dan!
Publicatie
Elliott Lieb & Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics Elsevier 1999.
[1] Anderzijds heeft de zogeheten Boltzmannentropie uit de statistische fysica de extra aanname nodig dat aan het begin van een proces systemen in een lage-entropietoestand verkeren.