Afbeelding 1. Newton en Leibniz.Isaac Newton (1643-1727) en Gottfried Wilhelm Leibniz (1646-1716) vlogen elkaar regelmatig in de haren.
Ronde 1: Differentiaalrekening – f’ vs. df/dx
Misschien komt het volgende je wel bekend voor. Als je in de wiskundeles leert differentiëren, worden er twee verschillende notaties door elkaar heen gebruikt. Het ene moment schrijft de leraar de afgeleide van de functie f naar de variabele x op als f’, en het volgende moment gebruikt de leraar de notatie df/dx. Deze twee verschillende manieren van schrijven hebben we te danken aan het feit dat de infinitesimaalrekening, waar differentiëren onderdeel van is, onafhankelijk ontwikkeld is door Isaac Newton en Gottfried Leibniz.
Al in de oudheid probeerden wiskundigen een methode te vinden om oppervlaktes en volumes te berekenen. Zo ontwikkelden de oude Grieken de uitputtingsmethode. Die methode benadert de onbekende oppervlakte van een figuur door deze figuur steeds nauwkeuriger in te vullen met een figuur waarvan de oppervlakte wel bekend is. Zo kun je bijvoorbeeld een cirkel benaderen met een veelhoek, waarbij geldt: hoe meer hoekpunten je veelhoek heeft, hoe nauwkeuriger je benadering wordt.
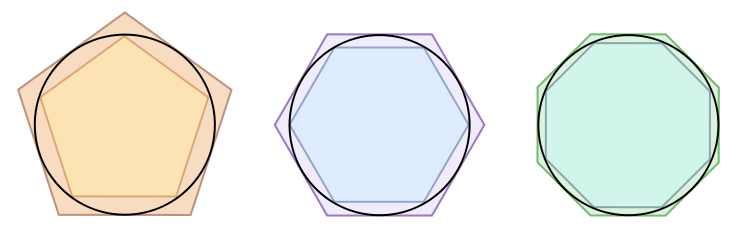
Afbeelding 2. De uitputtingsmethode.De benadering van een cirkel met behulp van veelhoeken. Afbeelding: Leszek Krupinski.
Differentiaalrekening kwam pas in de 17de eeuw echt tot wasdom. In de eerste helft van die eeuw werden nieuwe methodes ontwikkeld voor het berekenen van minima, maxima en raaklijnen, door wiskundigen zoals René Descartes en Pierre de Fermat, maar een allesomvattende methode voor differentiëren en integreren ontbrak nog.
De eerste die claimde zo’n methode te hebben gevonden was Isaac Newton (1643-1727) rond 1666. Hij gebruikte fluxions om de instantane verandering van een tijdsafhankelijke functie af te leiden. Hierbij gebruikte Newton oneindig kleine hoeveelheden tijd (geschreven als o) die toch niet nul zijn. Zo is de fluxion van de functie x = t2 op het punt t = 2 gegeven door de volgende formule:
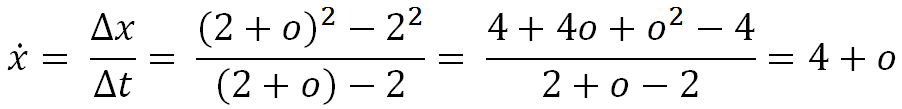
Wie kan differentiëren herkent hierin direct de gebruikelijke afgeleide. Newton gebruikte de resultaten van zijn methode voor het onderbouwen van zijn meesterwerk over de klassieke mechanica, de Philosophiae Naturalis Principia Mathematica. Zijn fluxionmethode leek dus een groot succes. Er was alleen een klein probleem. De Principia Mathematica verscheen pas in 1687 en Newton publiceerde pas in 1693 voor het eerst over zijn fluxions. In de tussentijd had iemand anders al een rivaliserende methode gepubliceerd.
De Duitser Gottfried Wilhelm Leibniz (1646-1716) was een academische alleskunner die zich onder andere heeft beziggehouden met filosofie, wetgeving, politiek, economie, logica en de wiskunde. Hij werd in 1672 aangespoord door de Nederlandse natuurkundige Christiaan Huygens om zich op de wiskunde te storten. Lang had hij niet nodig om tot nieuwe resultaten te komen. Uit zijn aantekeningen blijkt dat Leibniz al in 1675 aan het differentiëren was geslagen. Hij gebruikte de letter d voor differentiaal om oneindig kleine getallen aan te geven, zoals dx, en introduceerde het symbool ∫ (een uitgerekte letter s voor summa) om de oneindig lange sommaties in integralen aan te geven. Waar Newton verandering zag als een variabele grootheid over de tijd zag Leibniz verandering als het verschil over een reeks van waardes die oneindig dicht bij elkaar liggen.
I cannot proceed with the explanations of the fluxions now, I have preferred to conceal it thus: 6accdæ13eff7i319n4o4qrr4s8t12vz
Newton in een brief aan Leibniz
Nadat Newton en Leibniz enkele jaren elkaars werk hadden genegeerd, begon de controverse over wie de eer voor de ontwikkeling van de differentiaalrekening zou moeten krijgen pas na 1700. In 1704 werd er een anonieme recensie gepubliceerd over een werk van Newton waarin werd gesteld dat Newton zijn differentiaalrekening had gestolen van Leibniz. Veel wiskundigen waren het hier niet mee eens en de claim leidde er juist toe dat velen zich gingen afvragen of het omgekeerde niet waar was: dat Leibniz de ideeën van Newton had gestolen. Saillant detail: uiteindelijk bleek dat de recensie was geschreven door Leibniz zelf.
De discussie werd gedomineerd door Newton en zijn aanhangers, die Leibniz zagen als een oplichter. Zij vonden dat Leibniz alleen een nieuwe notatie had ontwikkeld voor ideeën die uiteindelijk van Newton waren. Opmerkelijk hierbij is dat Newtons claim dat hij zijn differentiaalrekening als eerste had ontwikkeld niet in twijfel werd getrokken, ondanks dat het enige bewijs hiervoor een weinig zeggende voetnoot was.
Over de jaren heen, en zelfs na de dood van de hoofdrolspelers, zijn er veel aantijgingen gedaan over en weer, maar hoe het precies zit is nooit helemaal duidelijk geworden. Er werd vooral Leibniz veel in de schoenen geschoven, maar een groot deel van de gemeenschap (zoals de Engelse Royal Society) was vanaf het begin bevooroordeeld in het voordeel van Newton. Wat dan weer in het voordeel van Leibniz spreekt, is dat de manier hoe hij tot zijn methode kwam sterk verschilde van die van Newton.
Hoe het ook zij, Leibniz won wel op één front. Zijn notatie bleek effectiever en wordt, tot op de dag van vandaag, veel meer gebruikt dan de notatie van Newton.
Ronde 2: Behoud van impuls vs. behoud van energie

Afbeelding 3. Impuls.Wat is het beste hulpmidde om de mechanica van biljartballen te beschrijven – impuls of energie?
De controverse tussen Newton en Leibniz over de ontwikkeling van de differentiaalrekening is zeker de beroemdste, maar ook op andere belangrijke punten waren de wetenschappers het niet met elkaar eens. Newton had zijn klassieke mechanica gebaseerd op het behoud van impuls. Alle drie de bewegingswetten van Newton gaan over kracht, wat niets anders is dan de verandering in impuls. Een uitleg over het behoud van impuls en de symmetrieën die ten grondslag liggen aan behoudswetten kun je hier lezen.
René Descartes was het met Newton eens en betoogde vóór het behoud van impuls. Het was Descartes waar Leibniz als eerste de aanval op opende. Leibniz beredeneerde aan de hand van simpele berekeningen met vallende stenen dat de keuze om impuls te definiëren als p = mv de verkeerde was. Neem het volgende voorbeeld: je laat een steen van 4 kg vallen vanaf een hoogte van 1 meter met een versnelling van 1 m/s. De steen heeft bij het raken van de grond een impuls van p = mv = 4 kg × 1 m/s = 4 kg m/s. Als je daarentegen een steen met een massa van 1 kg laat vallen vanaf een hoogte van 4 meter is deze steen volgens de wet van Galileo twee seconden onderweg en de steen raakt dan de grond met een snelheid van 2 m/s. Maar dit geeft een impuls van p = mv = 1 kg × 2 m/s = 2 kg m/s. Leibniz vond dat impuls juist die grootheid moest zijn die in deze gevallen hetzelfde antwoord zou geven. Hij liet met een even zo eenvoudige berekening, met dezelfde stenen, zien dat de grootheid die in deze situaties hetzelfde is niet p = mv is, maar p = mv2.
Maar wacht eens even… Leibniz had het niet over wat we vandaag de dag kennen als het behoud van impuls: hij had het over het behoud van energie!
In zijn dynamica maakte Leibniz onderscheid tussen twee ‘krachten’. De ‘levende kracht’, tegenwoordig bekend als kinetische energie, en de ‘dode kracht’, wat natuurlijk de potentiele energie is. Met behulp van dit onderscheid en aan de hand van het behoud van energie werkte Leibniz zijn eigen klassieke mechanica uit.
Maar wie had er nu gelijk, Newton (en Descartes) of Leibniz? Zoals wel vaker blijkt uit de geschiedenis van de natuurkunde zijn twee op het eerste gezicht elkaar uitsluitende opties helemaal niet zo exclusief. Zowel impuls als energie zijn behouden grootheden!
We hebben al twee rondes gehad, en nog steeds geen winnaar kunnen vaststellen. Hoewel toch ook hier, in ieder geval achteraf, Leibniz weer een plusje verdient. Waar Newtons behoud van impuls schitterde door wiskundige eenvoud en makkelijke toepasbaarheid bleek Leibniz’s behoud van energie een dieper gaande beschrijving te geven van de natuur. In de eeuw na Newton en Leibniz werd de klassieke mechanica verder uitgewerkt en dit project werd uiteindelijk bekroond met de wiskundige formalismen van Louis Lagrange en William Hamilton. Deze formalismen bouwen juist voort op het behoud van energie en zijn in de moderne natuurkundige theorieën, zoals de quantummechanica en de snaartheorie, niet meer weg te denken.
Ronde 3: De aard van ruimte – substantieel vs. relationeel
Afbeelding 4. Ruimtetijd.De relativiteitstheorie vertelt ons wat ruimte en tijd precies zijn. Hoe zage Newton en Leibniz dit?
Laatste ronde! Een ander punt waar Newton en Leibniz het niet over eens waren, was de aard van de ruimte. Dit vraagstuk kan in twee delen worden opgesplitst:
- Is lege ruimte nog steeds “iets”?
- Is niet-lege ruimte afhankelijk van wat erin zit?
Newton was een groot voorstander van het concept van absolute ruimte (zie deze link voor zijn argument). Hij beantwoordde de eerste vraag dan ook met een ‘ja’ en de tweede met een ‘nee’. Voor hem was de ruimte als het podium in een theater, ook aanwezig wanneer er niets wordt opgevoerd en, hoewel noodzakelijk, op geen enkele manier deelnemer aan het toneelstuk.
Leibniz beantwoordde de twee vragen, natuurlijk, precies omgekeerd. Zijn argumenten tegen de absolute ruimte van Newton zijn filosofisch van aard en maken ook gebruik van een god. Zo stelt Leibniz dat we het principe van “voldoende reden” moeten aannemen, dat zegt dat er een reden is dat God de wereld op deze manier heeft gemaakt en niet op een andere manier. Volgens Leibniz is er voor God in een wereld met absolute tijd geen reden om het universum te maken op het ene moment en niet een andere moment en is er in absolute ruimte geen reden om de wereld te scheppen met de ene oriëntatie of de andere oriëntatie. Maar dit schendt juist het principe van voldoende reden.
Volgens Leibniz is de ruimte niets meer dan een relatie tussen objecten. In een brief die hij schreef aan Samuel Clarke vergeleek Leibniz de ruimte met eem familiestamboom. Een stamboom bestaat niet zonder familieleden; het is juist het abstracte systeem van relaties tussen familieleden.
Wat het moderne antwoord op de twee vragen is, ligt er maar aan wie je het vraagt en vanuit welke theorie je het bekijkt. Laten we ons voor het gemak beperken tot het antwoord van Albert Einsteins algemene relativiteitstheorie. Einstein zou beide vragen met ‘ja’ beantwoorden. Volgens hem is lege ruimte zeker nog steeds “iets”, maar is de ruimte wel degelijk afhankelijk van wat erin zit. Die wisselwerking tussen ruimte en materie is juist Einsteins opvolger voor Newtons zwaartekracht. Hier kunnen we dan toch een kleine overwinning voor Newton noteren. Newton had het bij het rechte eind toen hij zei dat ruimte een “ding op zichzelf” is maar verkeek zich op de relatie tussen ruimte en materie. De relationele ruimte van Leibniz lijkt daarentegen geheel niet op de dynamische ruimte van Einstein.
Een winnaar?
Newton wordt algemeen beschouwd als een van de grootste wetenschappers aller tijden. In dit stuk is werk van Newton wat onderbelicht, maar de reden daarvoor is niet dat ik minder denk dan het allerbeste over het werk van Newton. (De persoon Newton schijnt overigens een stuk chagrijn te zijn geweest.) Newtons invloed op de natuurkunde is monumentaal en zijn meesterwerk, de Principia Mathematica, wordt gezien als de voltooiing van de wetenschappelijke revolutie. Als ik iets heb willen betogen is het dat er een ander is die juist niet de eer krijgt die hij mijns inziens ook verdient. Gottfried Wilhelm Leibniz: natuurkundige, wiskundige, filosoof en nog zoveel meer.
