Quantumcomputers (2): Encryptie, bits en qubits

Afbeelding 1. Bits, qubits en encryptie.Afbeelding: MaxPixel.

Encryptie

Stel dat jij, de lezer, mij een geheim bericht wil sturen over het internet, en dat ik me aan de andere kant van de Atlantische Oceaan bevind. Ondertussen probeert de rest van de wereld ons af te luisteren. Om er zeker van te zijn dat ik de enige ben die het bericht kan lezen, zou je het kunnen versleutelen: je slaat het bericht op in een bestand dat je alleen met een wachtwoord kunt openen.

Maar hoe vertel je mij het wachtwoord? Als je het mij simpelweg vertelt aan de telefoon of over het internet, kunnen potentiële luistervinken net zo goed het wachtwoord als het bericht zelf onderscheppen. Dat heeft dus helemaal geen zin.

Verassend genoeg is er een manier om berichten te versleutelen zonder van tevoren een wachtwoord af te spreken. Deze manier maakt gebruik van de ontbinding in priemfactoren en het verschil tussen ‘makkelijk’ en ‘moeilijk’. Wat ‘makkelijk’ en ‘moeilijk’ hier precies betekenen, bespraken we in deel 1 van deze serie.

Een priemgetal is een getal groter dan 1 dat alleen door zichzelf en 1 deelbaar is. De eerste vier priemgetallen zijn 2, 3, 5 en 7, maar er zijn er oneindig veel. In de wiskunde is er een stelling die zegt dat elk getal op een unieke manier geschreven kan worden als een product van priemgetallen. Dit product heet dan de ontbinding in priemfactoren of factorisatie van het getal. Bijvoorbeeld: 35 = 5 x 7. Priemgetallen zijn, per definitie, zelf niet meer te schrijven als product van twee andere priemgetallen. Zo zou je ze kunnen zien als de ondeelbare bouwstenen of atomen waaruit alle getallen zijn opgebouwd.

Het ontbinden in priemfactoren is een moeilijk probleem, in tegenstelling tot vermenigvuldigen. Vermenigvuldigen is namelijk makkelijk. De berekening 35 = 5 x 7 is dus moeilijk, terwijl de berekening 5 x 7 = 35 makkelijk is! Anders gezegd: we kunnen heen en weer tussen een getal en zijn ontbinding in priemfactoren, maar de ene kant op is dat moeilijk, en de andere kant op makkelijk.

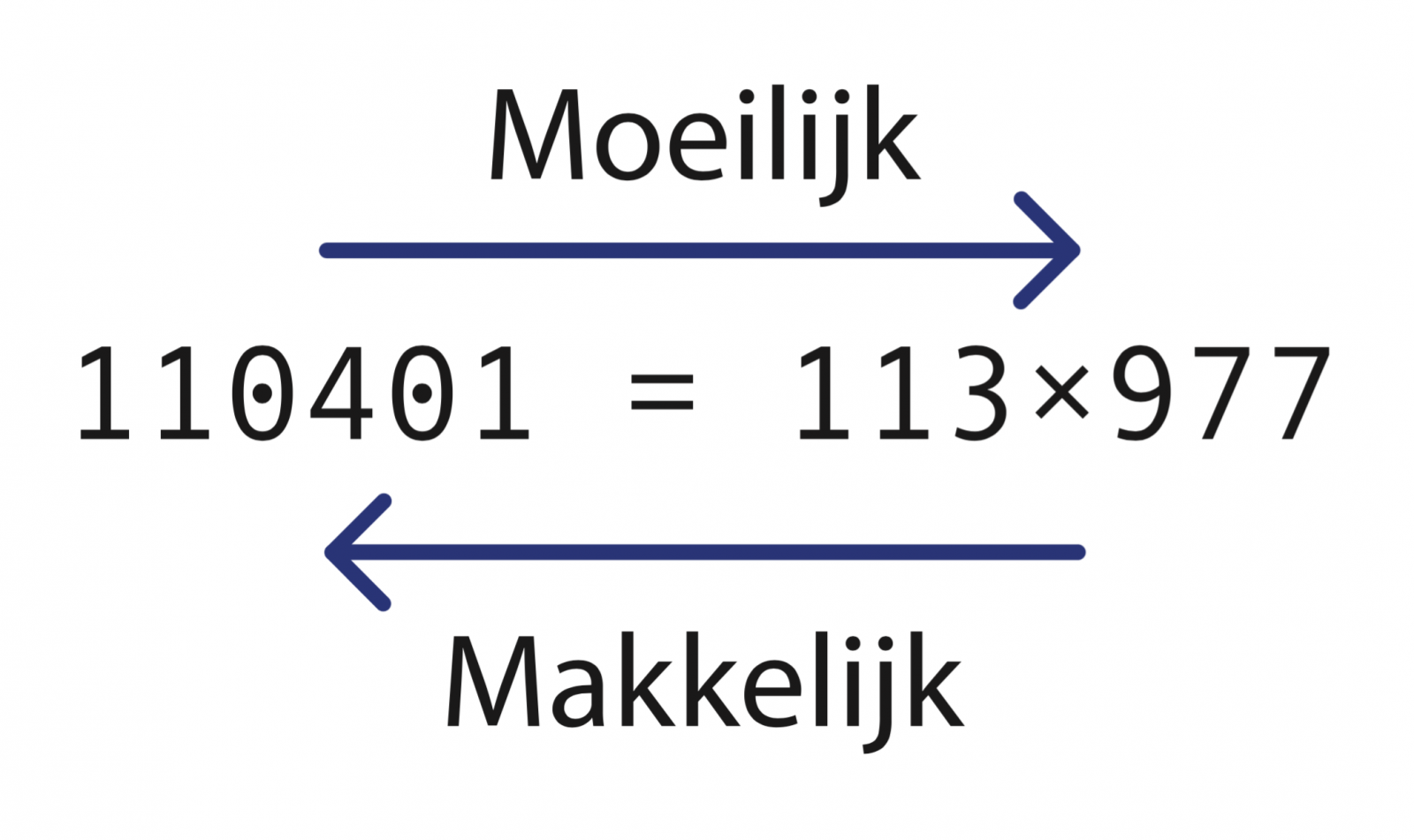
Afbeelding 2. Vermenigvuldigen en factoriseren.Een voorbeeld: de factorisatie van het getal 110401.

Hoe wordt dit nu gebruikt bij het versleutelen van een boodschap? Er bestaat een soort digitale kluis, met daarop een cijferslot, waar je digitale berichten in kunt doen. Hoe deze digitale kluis gemaakt wordt is voor ons verhaal niet zo belangrijk. Wat wel belangrijk is, is dat deze kluis de eigenschap heeft dat je een getal nodig hebt om hem dicht te doen, en dat deze kluis vervolgens alleen geopend kan worden met de priemfactoren waaruit datzelfde getal is opgebouwd.^[1]

Laten we teruggaan naar het voorbeeld waarin ik aan de andere kant van de Atlantische Oceaan zit en jij mij een geheim bericht wilt sturen zonder eerst een wachtwoord te hoeven doorgeven. We kunnen de kluis dan als volgt gebruiken. Allereerst neem ik twee priemgetallen met veel cijfers, bijvoorbeeld 977 en 113. (In werkelijkheid zijn de priemgetallen die worden gebruikt nog veel langer.) Deze vermenigvuldig ik met elkaar, dat geeft 110401, en dit getal stuur ik naar jou toe. Als iemand het getal 110401 onderschept is dat niet zo erg – ik zou het zelfs op mijn website kunnen zetten.

Dan stop jij het geheime bericht in de digitale kluis, die je op slot doet met het getal 110401, en deze kluis stuur jij vervolgens naar mij toe. Ik kan de kluis openen omdat ik de factoren weet waaruit 110401 is opgebouwd, namelijk 977 en 113. Ik ben de enige die deze factoren weet.

Luistervinken kunnen deze factoren echter ook achterhalen door het getal 110401 te factoriseren! De crux is nu, dat dat voor lange getallen praktisch onmogelijk is: factoriseren ligt voor gewone computers in de categorie ‘moeilijk’. Als ik twee erg lange getallen kies en vermenigvuldig, is het al snel ondoenlijk om het resulterende getal te factoriseren. Ik zou bijvoorbeeld twee priemgetallen kunnen kiezen die zo lang zijn dat het vinden van de factorisatie van het product langer duurt dan de gehele levensduur van de aarde.

Voor quantumcomputers ligt factorisatie echter in de categorie ‘makkelijk’. Het ligt dus eigenlijk in de tussencategorie ‘quantum-makkelijk‘: moeilijk voor een gewone computer maar makkelijk voor een quantumcomputer. Luistervinken met een quantumcomputer kunnen de kluis dus wel openmaken! Op dit moment heeft echter nog niemand een quantumcomputer die al zo goed werkt dat daarmee de kluis geopend kan worden.

Een belangrijk punt hebben we tot nu toe niet besproken. Hoe is het mogelijk dat sommige problemen voor gewone computers moeilijk zijn, terwijl ze voor quantumcomputers makkelijk zijn? Het antwoord is dat quantumcomputers op een fundamenteel andere manier werken. Ze maken namelijk gebruik van de bijzondere eigenschappen van de quantummechanica. Waar een normale computer met bits werkt, werkt een quantumcomputer met quantummechanische bits: de zogenaamde qubits.

Bit vs. qubit

Het gedrag van alledaagse objecten, zoals stoelen, planeten en appels, wordt beschreven door de klassieke mechanica, zoals je die ook op de middelbare school leert. Het gedrag van heel kleine objecten, zoals atomen en moleculen, wordt echter beschreven door de quantummechanica. Quantummechanisch gedrag kan voor mensen heel tegenintuïtief zijn omdat wij veel groter zijn dan atomen of moleculen. Alle objecten waar wij ooit mee te maken hebben gehad, gedragen zich volgens de regels van de klassieke mechanica, en niet volgens de quantummechanica.

Het belangrijkste verschil tussen de klassieke en de quantummechanica is dat objecten in de quantummechanica in een zogenaamde superpositie kunnen zijn die weer verdwijnt zodra we het object meten. Dit zullen we verderop in dit artikel nog verder uitleggen. Meer informatie hierover kan je ook vinden in andere artikelen op deze website, zoals hier of hier.

Voorlopig blijven we even bij de klassieke mechanica. Het gedrag van bits in een gewone computer wordt namelijk beschreven door de klassieke mechanica. Een bit is, heel simpel gezegd, een ‘ding dat twee dingen kan zijn’. Hierbij zou je kunnen denken aan een dambord met geen of één steen erop, een wijzer die alleen omhoog of omlaag kan wijzen, of een draad waar een stroom doorheen loopt of juist niet.

In deze voorbeelden is er steeds sprake van een systeem (dambord en damsteen, wijzer, draad) en twee mogelijke toestanden (wel of niet op het bord, omlaag of omhoog, stroom of geen stroom). In wat volgt maakt het ons eigenlijk niet uit welk systeem de bit vormt. Daarom zullen we het heel algemeen over een ‘bit’ hebben, en de twee verschillende toestanden ‘0’ en ‘1’ noemen. Als je wilt kun je altijd denken aan een wijzertje dat alleen omhoog of omlaag kan staan.

We kunnen de mogelijke toestanden van een systeem visualiseren door voor elk van die toestanden een punt op een vel papier te zetten. De figuur die je zo krijgt heet de toestandsruimte van het systeem. Voor een bit wordt de toestandsruimte dus gevormd door twee punten. Het ene punt hebben we ‘0’ genoemd en het andere ‘1’. We kunnen bovendien de huidige toestand aanwijzen met een pijl.

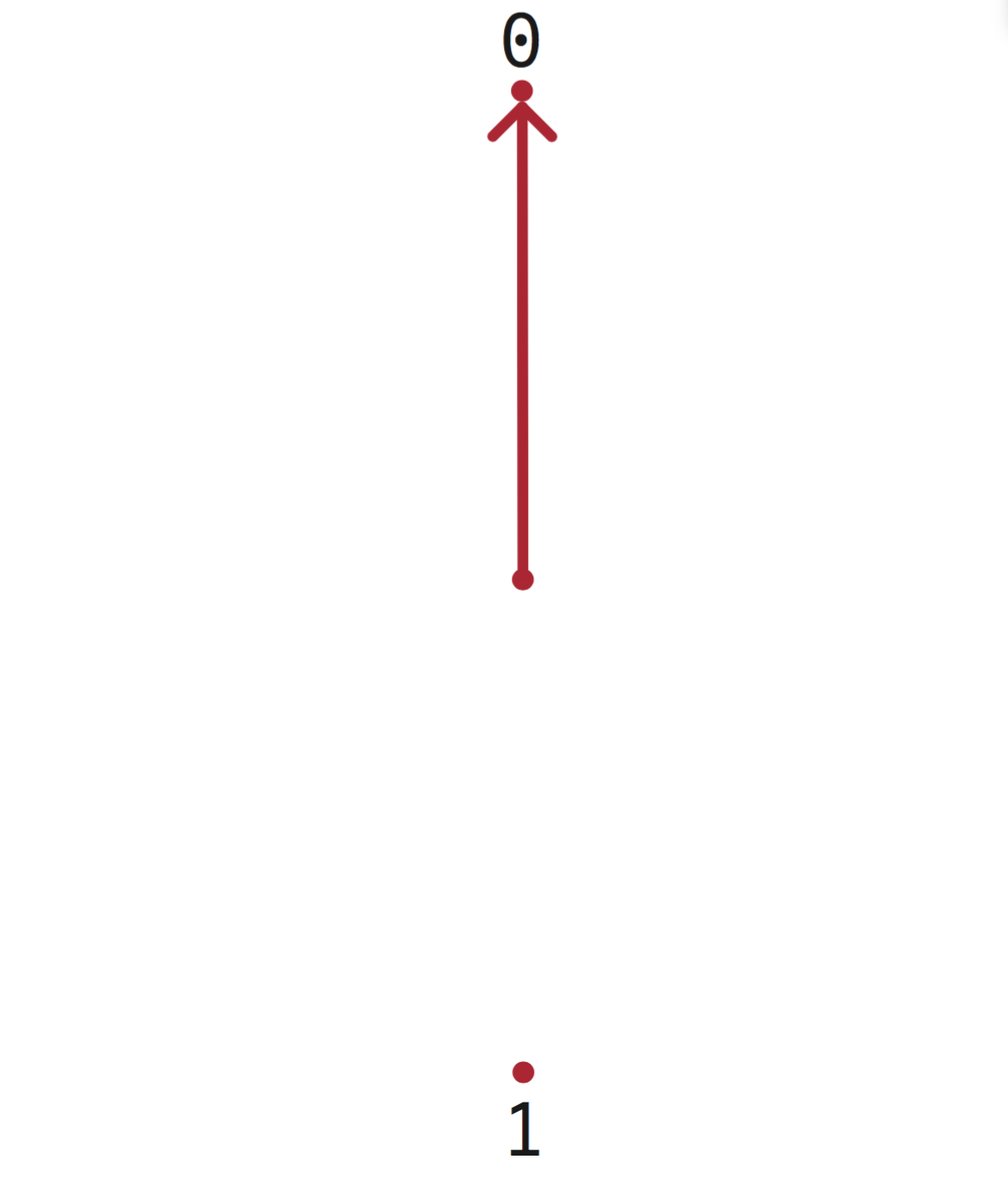
Afbeelding 3. Een bit.De toestandsruimte van een bit.

We kunnen nu al het bovenstaande als volgt samenvatten:

Een bit is een klassiek systeem waarvan de toestandsruimte gevormd wordt door twee punten.

Dankzij deze bondige definitie kunnen we nu heel kort zijn over de qubit:

Een qubit is een quantummechanisch systeem waarvan de toestandsruimte het oppervlak van een bol is.

Ook voor de qubit kunnen we de toestandsruimte tekenen en de huidige toestand aangeven met een pijl, bijvoorbeeld zo:

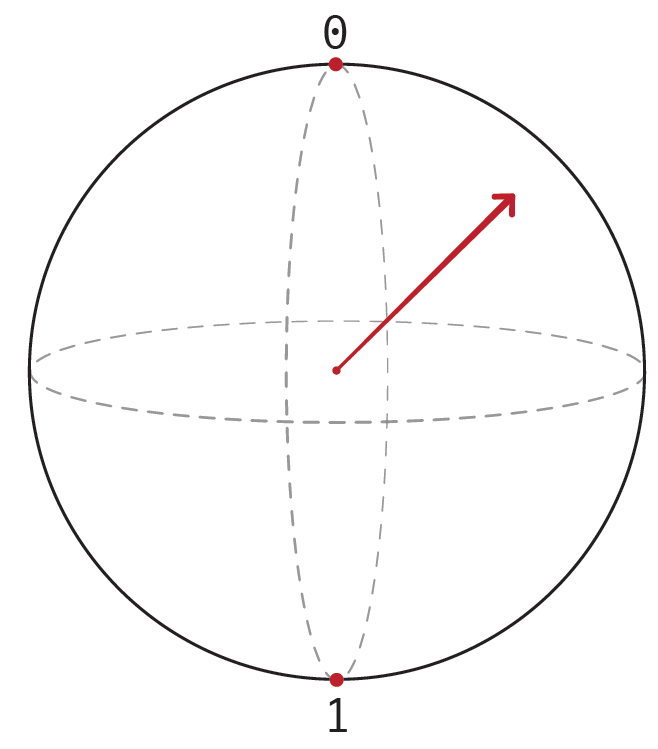
Afbeelding 4. De Blochbol.De toestandsruimte van een qubit.

De toestanden ‘0’ en ‘1’ zijn nu dus nog maar twee van de vele mogelijke toestanden. De bol van toestanden noemt men de Blochbol, naar zijn bedenker Felix Bloch.

We hebben bij de definitie van de qubit slinks de vraag ontweken wat nu de quantummechanische damborden, wijzers of draden zijn waarmee je zo’n qubit maakt. Het antwoord op die vraag zullen we pas in deel drie van dit dossier behandelen. Voor qubits geldt echter, net als voor bits, dat het nu niet zoveel uitmaakt hoe ze daadwerkelijk gemaakt worden. Voor nu kun je denken aan een wijzer die alle kanten op kan wijzen, en bovendien zò klein is dat die zich quantummechanisch gedraagt.

Maar wat is dat quantummechanische gedrag? Naast dat de pijl nu in alle richtingen kan wijzen is er een ander fundamenteel verschil: als we de qubit meten, is hij na deze meting altijd direct in de toestand 0 òf 1, en nooit iets daartussenin. Door het meten van de qubit verstoren we dus altijd zijn toestand. Helaas is het fundamenteel onmogelijk om de qubit te meten zonder deze verstoring te veroorzaken. Ik kan je niet uitleggen wat precies de reden van deze verstoring is. Sterker nog: dat kan niemand. Het interpreteren van het ‘ineenstorten van de golffunctie’, zoals dit effect genoemd wordt, is nog een van de onbegrepen zaken in de quantummechanica.

Wat we wel precies weten is de kans dat we een bepaalde meetuitkomst krijgen: hoe meer de pijl in de richting van de 0 staat, hoe groter de kans is dat we meetuitkomst 0 krijgen en de pijl na deze meting dus recht op de 0 staat. Hetzelfde geldt voor 1.^[2]

Als de pijl naar rechts wijst, dus als de qubit in de toestand ‘→’ is, wijst de pijl net zomin naar de 0 als naar de 1. De kans op meetuitkomst 0 is dus net zo groot als de kans op meetuitkomst 1: allebei 50%. Na deze meting staat de pijl recht op de 0 of de 1, afhankelijk van wat de meetuitkomst was. Dit is wat mensen bedoelen als ze zeggen dat een qubit in een superpositie is, of dat ‘een qubit een 0 en een 1 tegelijk’ is. De qubit is altijd maar in één toestand, maar als je de qubit meet zijn er twee mogelijke uitkomsten.

Computer vs. quantumcomputer

Laten we nu eens kijken naar meerdere bits.  Als we aan de eerste bit een tweede toevoegen, hebben we in totaal vier mogelijke toestanden: 00, 01, 10 en 11. We kunnen de toestandsruimte van de twee bits dus visualiseren met vier punten:

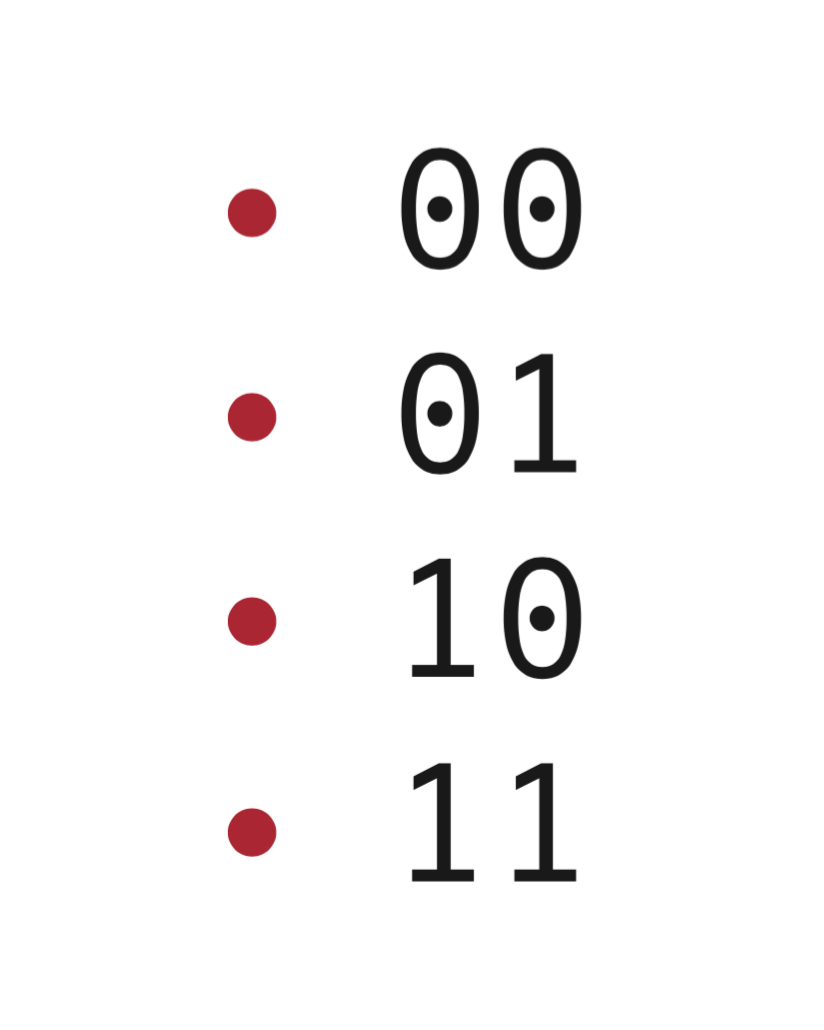
Afbeelding5. Twee bits.De toestandsruimte van twee bits.

Voor drie bits hebben we nog eens twee keer zoveel toestanden, dus acht in totaal. We kunnen steeds de waarden van de drie bits gebruiken als label voor elk van deze toestanden. We kunnen daar echter ook de normale getallen voor gebruiken:

Afbeelding 6. Drie bits.De toestandsruimte van drie bits, samen met normale getallen als labels.

In het algemeen hebben n bits 2ⁿ verschillende toestanden. Op deze manier kunnen we alle getallen ‘maken’ zolang we maar genoeg bits hebben. Als je met bits een getal hebt geschreven, noemt men dat de binaire representatie van een getal.

Een computer is in essentie een machine die een reeks bits als input neemt, en een op een controleerbare manier een andere reeks bits als output geeft. Een voorbeeld is een computer die als taak heeft de kleinste priemfactor te vinden van een getal. Als we het getal (110401) als input zouden geven, dan komt de kleinste priemfactor (113) eruit.

Als we aan de toestandsruimte denken die groot genoeg is om alle getallen van (0) t/m (110401) weer te kunnen geven^[3], dan is het alsof we vóór de berekening een pijl hadden die naar (110401) wees. Na de berekening wijst deze pijl naar (113).

Elke berekening, hoe moeilijk ook, kan worden opgedeeld in kleine stapjes. Een goed voorbeeld daarvan is het algoritme voor optellen zoals we dat in deel 1 gezien hebben. Om twee heel grote getallen bij elkaar op te tellen, hoef je maar twee dingen te kunnen: twee getallen van maar één cijfer bij elkaar optellen, en ‘onthouden’. (Als je de getallen in binaire vorm zou krijgen, zou je zelfs alleen maar in staat hoeven te zijn om 0 of 1 bij 0 of 1 op te tellen, en te onthouden.)

Eén van de vele stappen van een algoritme in het algemeen kan de volgende zijn: ‘doe niets als de eerste bit een 0 is, maar verander de tweede bit als de eerste bit een 1 is’. Dit stapje wordt in bijna elk algoritme gebruikt, en heeft daarom een eigen naam: de CNOT-gate. Zoals je nu zelf zou kunnen uitvogelen, wordt in deze stap de toestand 00 veranderd in 00, 01 in 01, 10 in 11 en 11 in 10.

In termen van de toestandsruimte gebeurt er dus, als we bijvoorbeeld beginnen met de input 10, het volgende:

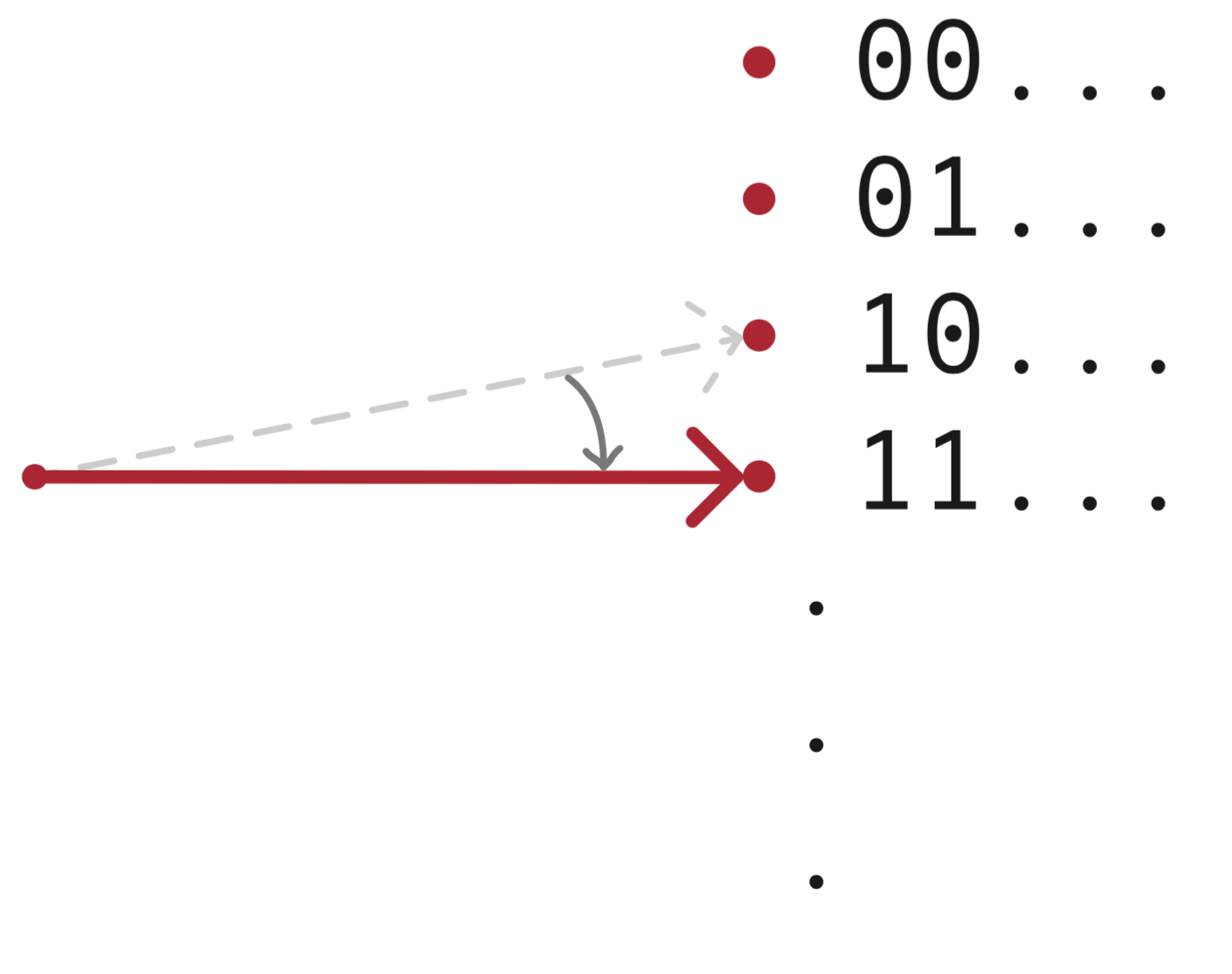
Afbeelding 7. CNOT.De actie van de CNOT-gate op de toestandsruimte als de huidige toestand begint met 10.

Naast dit voorbeeld zijn er nog allerlei andere kleine stappen die in een algoritme voor kunnen komen. Na heel veel van dit soort kleine stappen wijst de pijl uiteindelijk naar het juiste antwoord.

Nu we min of meer weten hoe een computer werkt kunnen we over naar de quantumcomputers. Net zoals een computer werkt met meerdere bits, werkt een quantumcomputer met meerdere qubits. De toestandsruimte van meerde qubits is echter heel lastig voor te stellen. Voor twee qubits hebben we al een zesdimensionale toestandsruimte!

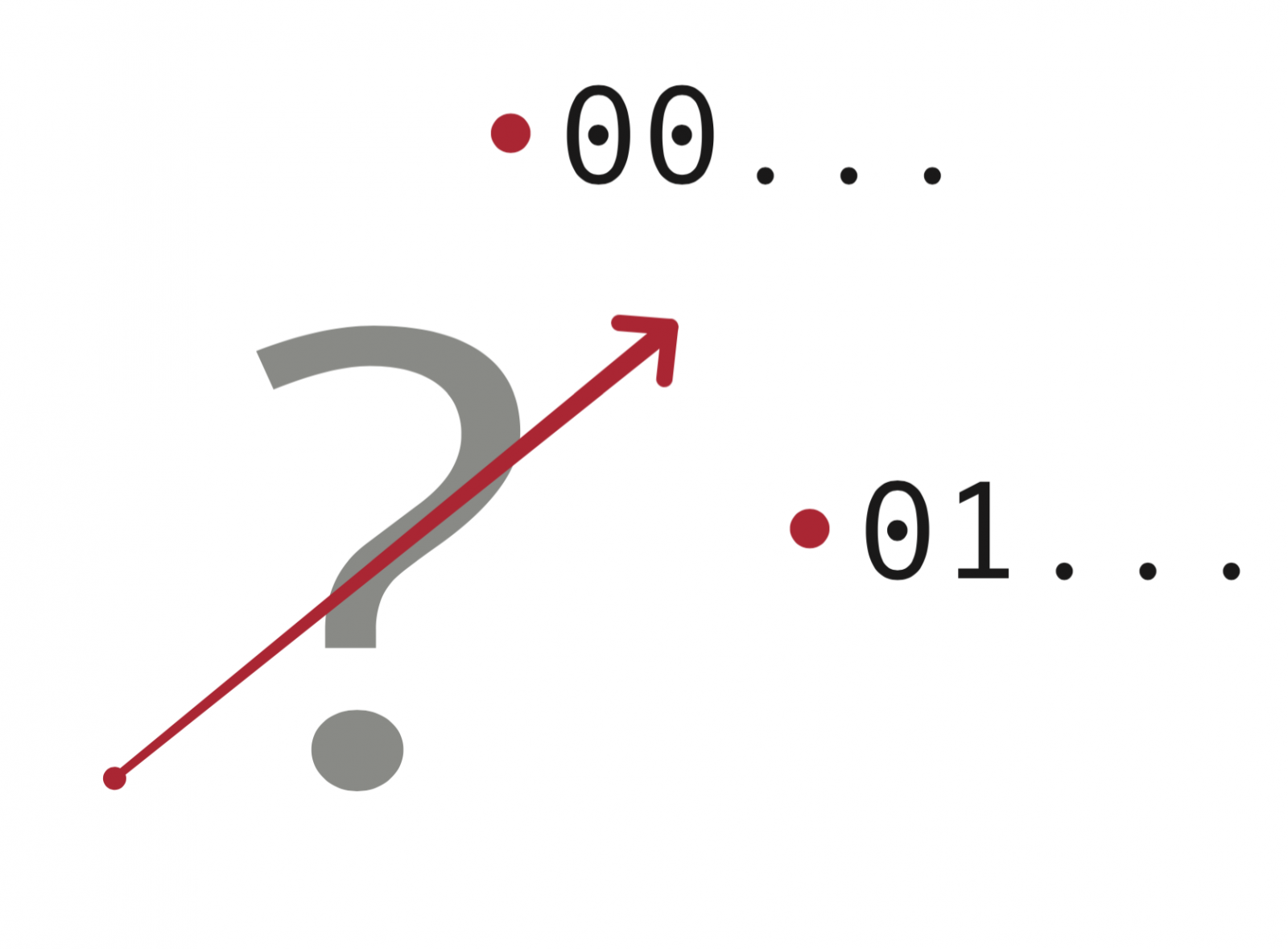
Afbeelding 8. Twee qubits.De toestandsruimte van twee qubits is zesdimensionaal. Kun jij je dat nog voorstellen?

Als je zo’n zesdimensionale toestandsruimte niet meer kunt voorstellen is dat helemaal niet erg.^[4] Wat belangrijk is, is dat als we de twee qubits meten, de pijl één van de toestanden 00, 01, 10, of 11 aanwijst.

In het algemeen geldt dat de toestand van n qubits gezien kan worden als een punt in een (2ⁿ-2)-dimensionale ruimte. Als we al deze qubits meten vinden we na deze meting altijd een punt dat we kunnen aangeven met enen en nullen.

We zijn dan nu eindelijk aangekomen bij de hamvraag van dit dossier, namelijk: wat is een quantumcomputer? Een quantumcomputer is een machine die het eindpunt van de pijl in de toestandsruimte van n qubits op een bestuurbare manier verplaatst.

Zo kunnen we met een quantumcomputer problemen oplossen. We kunnen dat doen door hem een klassieke input te geven. Dat wil zeggen: we beginnen met een pijltje recht op een punt dat wordt aangegeven met enen en nullen. Na de berekening wijst de pijl naar een ander punt in de toestandsruimte. Als we nu alle qubits meten, vinden we een klassieke uitkomst.

We kunnen bijvoorbeeld een quantumcomputer nemen die als taak heeft de kleinste priemfactor van het inputgetal te vinden. We zetten de pijl dan recht op de toestand (110401). De quantumcomputer doet dan zijn berekeningen, en als we aan het eind de qubits meten, vinden we dat het punt (113) wordt aangewezen. De vraag (input) en het antwoord (output) waren allebei klassiek, maar tijdens de tussenstappen was de toestand quantummechanisch.

Waarom zorgt dit er nu voor dat sommige problemen, zoals factoriseren, in de categorie quantum-makkelijk vallen? (Ter herinnering: quantum-makkelijk is de categorie: ‘moeilijk voor een computer maar makkelijk voor een quantumcomputer’.) Dat komt voornamelijk door het zogenaamde quantumparallelisme.

Net als bij een normale computer kan elke quantumberekening worden opgedeeld in kleine stapjes. Bij de normale computer was een voorbeeld van zo’n klein stapje de CNOT-gate. Een quantumcomputer gebruikt ook precies zo’n CNOT-gate als tussenstapje, maar dan natuurlijk quantummechanisch.

Laten we beginnen met de overeenkomsten. Als de pijl tijdens de quantumberekening precies op de stand 10 staat, staat deze na de CNOT-gate, net zoals in het klassieke geval, precies op de stand 11. Dit geldt ook zo voor de andere mogelijke klassieke inputs.

Het verschil is, dat bij een quantumcomputer de input-pijl niet precies op 00, 01, 10 of 11 hoeft te staan. Het mag ook overal daartussenin staan. Het antwoord van de CNOT-gate is dan ook een pijl die tussen alle antwoorden in staat, hoewel de quantumcomputer maar één berekening heeft gedaan, en niet vier! Precies dit gedrag zorgt ervoor dat sommige problemen in de categorie quantum-makkelijk vallen.

Het lijkt dus alsof er door de quantumcomputer in één stap vier berkeningen tegelijkertijd, oftewel parallel, gedaan zijn. Het is echter niet zo, dat we per stap ook de toegang hebben tot alle mogelijke antwoorden van die stap! Als we namelijk de qubits meten, op welk moment dan ook, dan vinden we maar één antwoord, en niet vier.

De manier waarop quantumcomputers verschillende berekeningen tegelijkertijd kunnen doen, zit dus ergens tussen parallel en niet-parallel in. Aangezien deze vorm van parallelisme komt door de quantummechanische eigenschappen van de qubits noemen we dit quantumparallelisme. De kunst is dus om een algoritme voor een quantumcomputer zó te ontwerpen dat je begint met een klassiek getal, onderweg zo veel mogelijk verschillende ‘mogelijkheden bekijkt’, en eindigt met een klassieke oplossing of een superpositie van een aantal van zulke oplossingen. Dit is wat mensen bedoelen als ze zeggen dat een quantumcomputer sneller is omdat die ‘alles tegelijk’ kan uitrekenen.

Dit lijkt misschien allemaal sciencefiction, maar het is echt gewoon science. Er worden op dit moment (2017) al quantumcomputers gebouwd met 5 qubits die onder andere de CNOT-gate kunnen uitvoeren. Sterker nog: je kunt inloggen op deze website en zelf een quantumcomputer een CNOT-gate laten uitvoeren!

Kunnen alle geheime berichten nu gekraakt worden? Zo ver is het gelukkig nog lang niet. Voor een quantumcomputer die encryptie kan breken zijn heel veel qubits nodig – minstens enkele duizenden. Ook moeten er veel rekenstappen gemaakt kunnen worden zonder dat de pijl per ongeluk ergens fout wordt neergezet.

Wat de beste manier is om dit te bereiken, is nog lang niet duidelijk. Er zijn verschillende onderzoeksgroepen, met elk hun eigen methoden. Welke methode zal er als winnaar uit de bus komen? Meer hierover lees je in het volgende deel van dit dossier.

Deel drie van dit dossier verschijnt op vrijdag 14 april.

^[1]We bespreken hier het RSA-encryptiealgoritme.

^[2]Voor de geïnteresseerden: de kans op uitkomst ‘0’ is P(0) = cos²(θ/2), waar θ de hoek is tussen de pijl en het punt ‘0’. Omdat kansen altijd optellen tot 1, en cos²(θ/2) + sin²(θ/2) = 1, geldt automatisch dat P(1) = sin²(θ/2).

^[3]Als oefening: hoeveel bits zou je minimaal nodig hebben om een getal tussen 0 en 110401 weer te kunnen geven? Een groepje van 8 bits wordt een byte genoemd. Hoeveel bytes heb je nodig? (Hierbij mag je gerust naar boven afronden). Hoeveel van dit soort getallen kun je opslaan als je een gigabyte (10⁹  bytes) aan geheugen hebt?

^[4]Je kunt je als volgt bijvoorbeeld een zesdimensionale bol voorstellen. Als je op de aarde staat, een bol met een tweedimensionaal oppervlak, kun je twee lijnen op de grond tekenen die een hoek van 90° maken. Een lijn erbij tekenen die met alle twee van deze lijnen een hoek van 90° maakt gaat niet omdat het oppervlak van de aarde slechts tweedimensionaal is. Voor beide lijnen geldt, dat als je maar lang genoeg in de richting van die lijn blijft lopen, je weer uitkomt waar je begonnen was. (Hierbij nemen we natuurlijk aan dat de aarde prefect rond is, en je perfect in een rechte lijn kunt blijven lopen.) Op een zesdimensionale bol kun je zes lijnen teken, waarvoor geldt dat ze allemaal een hoek van 90° met alle andere lijnen maken, en je door elke lijn te volgen uiteindelijk weer bij hetzelfde punt uitkomt.