Quantumzwaartekrachtprobleem

De algemene relativiteitstheorie van Albert Einstein en het standaardmodel van elementaire deeltjes behoren tot de grootste, meest succesvolle theorieën van de theoretische natuurkunde. Het standaardmodel is een quantumtheorie, die uitlegt hoe alle elementaire deeltjes (dat wil zeggen: onsplitsbare deeltjes) die ons bekend zijn, met elkaar wisselwerken en zich gedragen onder drie van de vier fundamentele krachten uit de natuur: de elektromagnetische kracht en de zwakke en sterke kernkrachten. In het standaardmodel worden deze drie krachten gequantiseerd. Dit betekent dat de deeltjes die de kracht overbrengen (bijvoorbeeld fotonen/lichtdeeltjes voor de elektromagnetische kracht), in de theorie quantumdeeltjes zijn, die discrete waardes voor hun energie en impuls kunnen hebben en niet als een puntdeeltje, maar als een golffunctie beschreven moeten worden, waarvan de impuls en de positie niet tegelijkertijd exact kunnen worden vastgesteld. Daarnaast is het standaardmodel niet zomaar een quantummechanische theorie, maar een quantumveldentheorie. Dit wil zeggen dat de theorie verenigbaar en dus niet in conflict is met de speciale relativiteitstheorie, die stelt dat de snelheid van het licht hetzelfde is voor iedereen die met een constante snelheid beweegt.

De algemene relativiteitstheorie is een uitbreiding van de speciale relativiteitstheorie die ook versnellende personen en objecten beschrijft. In het bijzonder is de algemene relativiteitstheorie een zwaartekrachtstheorie, die zegt hoe de aanwezigheid van massa de ruimte en tijd kan krommen. Deze kromming van ruimtetijd door massa is een lastig voorstelbaar concept. Het wordt vaak visueel gemaakt zoals in afbeelding 2. Hier wordt de kromming van een plakje tweedimensionale ruimte door de aanwezigheid van de aarde, weergegeven aan de hand van een tweedimensionaal rooster. Deze kromming betekent fysisch dat een lichtstraal die ergens over dat plakje beweegt, de kromming van het plakje zal volgen. Wanneer de lichtstraal langs de aarde scheert, zal deze de ruimtekromming volgen en dus een beetje afbuigen, om de aarde heen. Dit effect, van het buigen van het licht om zware objecten heen, is experimenteel aangetoond en is een goede test voor de juistheid van de algemene relativiteitstheorie.

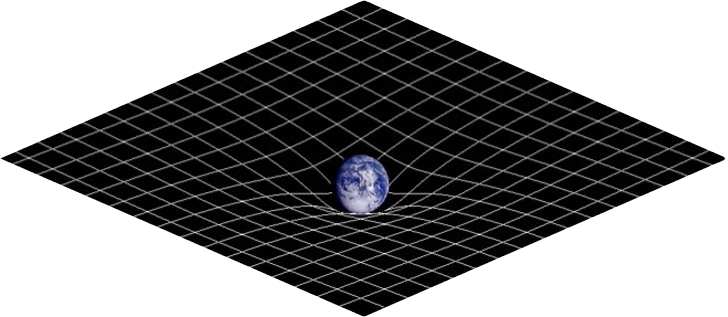
Het liefst zou ik in afbeelding 2 naast het tweedimensionale ruimteplakje ook de derde ruimtedimensie en de tijdsdimensie visueel weergeven, om niet alleen de kromming van ruimte maar ook van ruimtetijd intuïtief te maken, maar je begrijpt misschien wel dat dit erg lastig weer te geven is op een tweedimensionaal beeldscherm.

Nu ik de algemene relativiteitstheorie en het standaardmodel in grote lijnen heb beschreven, komen we tot het beantwoorden van de vraag of, en zo ja, waarom, deze twee theorieën in conflict zijn. Merk op dat beide theorieën succesvolle voorspellingen hebben gedaan die door verschillende experimenten bevestigd zijn. Het liefst zouden we dus zeggen dat beide theorieën ‘correct’ zijn. Zoals we in de natuurkunde, en ook in andere wetenschapsgebieden, echter al zo vaak hebben ondervonden, geven nieuwe natuurkundige theorieën ons weliswaar nieuwe inzichten, voorspellingen en concrete technologische toepassingen, maar blijkt vaak dat de werkelijkheid toch nóg genuanceerder en ingewikkelder is, en dat we onze theorie moeten aanpassen of uitbreiden om de werkelijkheid nog beter te beschrijven en begrijpen.

Het is dus goed mogelijk, en – gegeven meerdere fenomenen waar onze huidige natuurkundige theorieën nog geen antwoord op kunnen geven – zelfs waarschijnlijk, dat het standaardmodel en de algemene relativiteitstheorie niet de ‘eindtheorieën’ van het universum zijn. Naast een historische en fenomenologische motivatie voor het bestaan van een theorie buiten of boven deze twee krachtige theorieën, bestaat er ook een theoretische motivatie. Deze heeft te maken met het quantumzwaartekrachtprobleem: het ‘conflict’ tussen quantumtheorie en zwaartekracht, en daarmee tussen het standaardmodel, onze beste quantumtheorie, en algemene relativiteitstheorie, onze beste zwaartekrachtstheorie.

Het quantumzwaartekrachtprobleem neemt ten minste twee vormen aan. Allereerst worden in het standaardmodel, zoals ik net al noemde, drie van de vier fundamentele krachten gequantiseerd. Aangezien de quantumbeschrijving van deze drie krachten tot op grote precisie overeen blijkt te komen met de werkelijkheid, is het niet gek om te denken dat de vierde fundamentele kracht, namelijk de zwaartekracht, ook een quantumkracht is, en dat de kracht dus overgebracht wordt door een quantumdeeltje. Voor de zwaartekracht wordt dit quantumdeeltje ook wel het graviton genoemd. Zoals in detail uitgelegd in dit Quantum Universe-artikel is het vooralsnog echter een theoretische uitdaging om de zwaartekracht te quantiseren. Het graviton heeft andere eigenschappen dan de overbrengers van de andere krachten – in het bijzonder heeft het een ander impulsmoment (oftewel: een andere spin) – en die maken het wiskundig veel moeilijker om een quantumtheorie van de zwaartekracht te formuleren. Er bestaat momenteel dan ook nog geen theorie die zowel de experimenteel bevestigde voorspellingen van het standaardmodel reproduceert als ook de zwaartekracht quantiseert. Quantumfysica en zwaartekracht zijn daarmee niet verenigd in één theorie: we hebben nog geen volledige theorie van quantumzwaartekracht.

Het quantumzwaartekrachtprobleem neemt echter een tweede vorm aan, wanneer je kijkt naar de onderliggende principes van de quantumtheorie en de algemene relativiteitstheorie. Nobelprijswinnaar Roger Penrose, beschreef in zijn artikel On Gravity’s role in Quantum State Reduction uit 1996 dat deze principes met elkaar in conflict zijn. Voor de eenvoud beschreef hij het conflict tussen quantummechanica en algemene relativiteitstheorie. Het conflict tussen quantumveldentheorie, de speciaal-relativistische uitbreiding van quantummechanica, en algemene relativiteitstheorie zou vergelijkbaar zijn.

Het probleem komt volgens Penrose aan het licht als je een zogeheten superpositie van verschillende ruimtetijden bekijkt. Dit betekent dat je een ruimtetijdconfiguratie (dat wil zeggen: een kromming van de ruimtetijd zoals in afbeelding 2) als onderdeel van een quantumtoestand ziet. Quantumtoestanden kunnen in superpositie zijn, wat intuïtief bijvoorbeeld wil zeggen dat één object op meerdere plekken tegelijk is, of verschillende impulsmomenten tegelijk heeft. Een superpositie van ruimtetijden zou dan bijvoorbeeld een toestand zijn zoals degene die ik \( \psi_0 \) noem in de schematische weergave in afbeelding 3, waar de aarde (met bepaalde gewichten die volgen uit de getallen \( \alpha \) en \( \beta \)) op twee verschillende plekken is en waar als gevolg de twee ruimtetijden niet hetzelfde zijn.^[1]

Een probleem ontstaat nu als we willen achterhalen hoe een of ander klein object, in afbeelding 4 weergegeven als een oranje bal, zal gaan bewegen in deze superpositie van ruimtetijden.

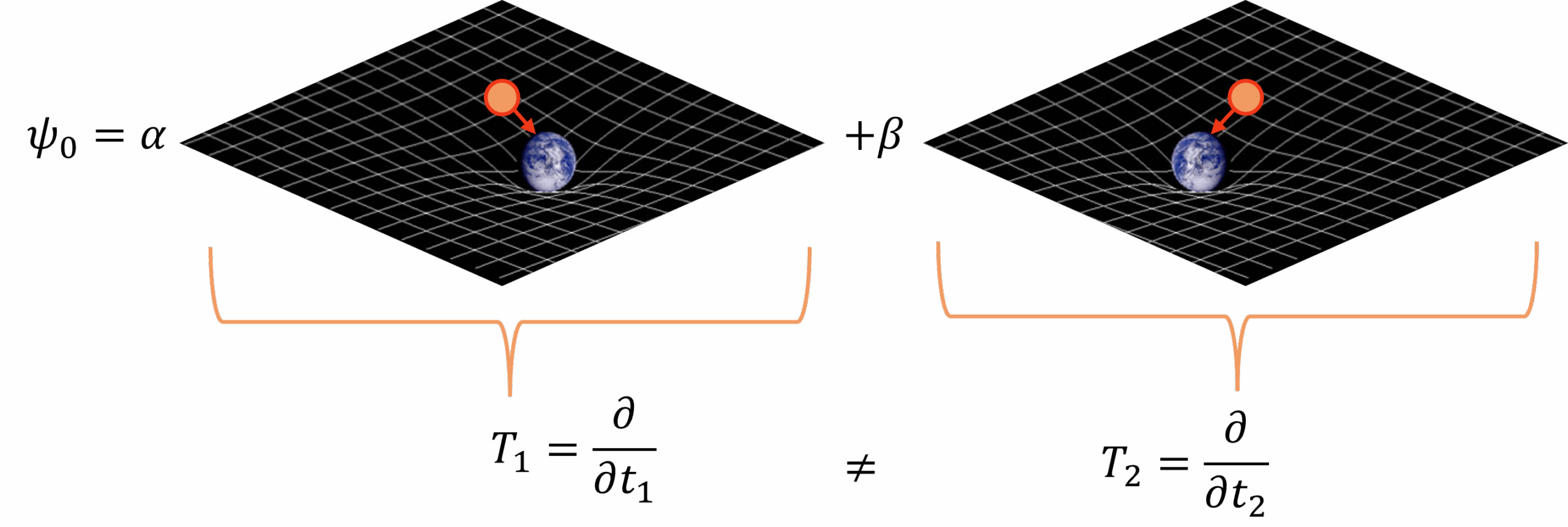
In de linker toestand, zal de oranje bal naar rechtsonder, in de richting van de aarde bewegen. In de rechter toestand, zal de bal zich echter in gedeeltelijk tegengestelde richting, naar linksonder bewegen, waar de aarde zich bevindt. Omdat deze ruimtelijke richtingen niet hetzelfde zijn, blijkt nu uit de wetten van de algemene relativiteitstheorie dat ook de richting die we ‘de tijdsrichting’ noemen – onder de afbeelding in de wiskundige notatie weergegeven met \( T_1 \) en \( T_2 \) – verschillend is voor de twee toestanden. In formules: \( T_1 \neq T_2 \), de tijdsrichtingen zijn verschillend!

In het formalisme van de quantummechanica kan er echter maar één tijdsrichting bestaan, volgens welke alle quantumtoestanden evolueren. Kunnen we in de bovenstaande situatie een enkele tijdsrichting consistent definiëren? Penrose laat zien dat het antwoord op deze vraag ‘nee’ is. Een naïeve oplossing zou zijn om de tijdsrichting te definiëren als het gemiddelde van de twee tijdsrichtingen in afbeelding 4. Dit laat ik zien in het onderste plaatje van afbeelding 5, waar de twee ruimtetijden als het ware op elkaar gelegd worden. Hierdoor is de kromming van de aarde op twee verschillende plekken aanwezig. Het balletje zal nu naar beneden bewegen en er is nog maar één tijdsrichting – zoals gewenst, zal je misschien denken.

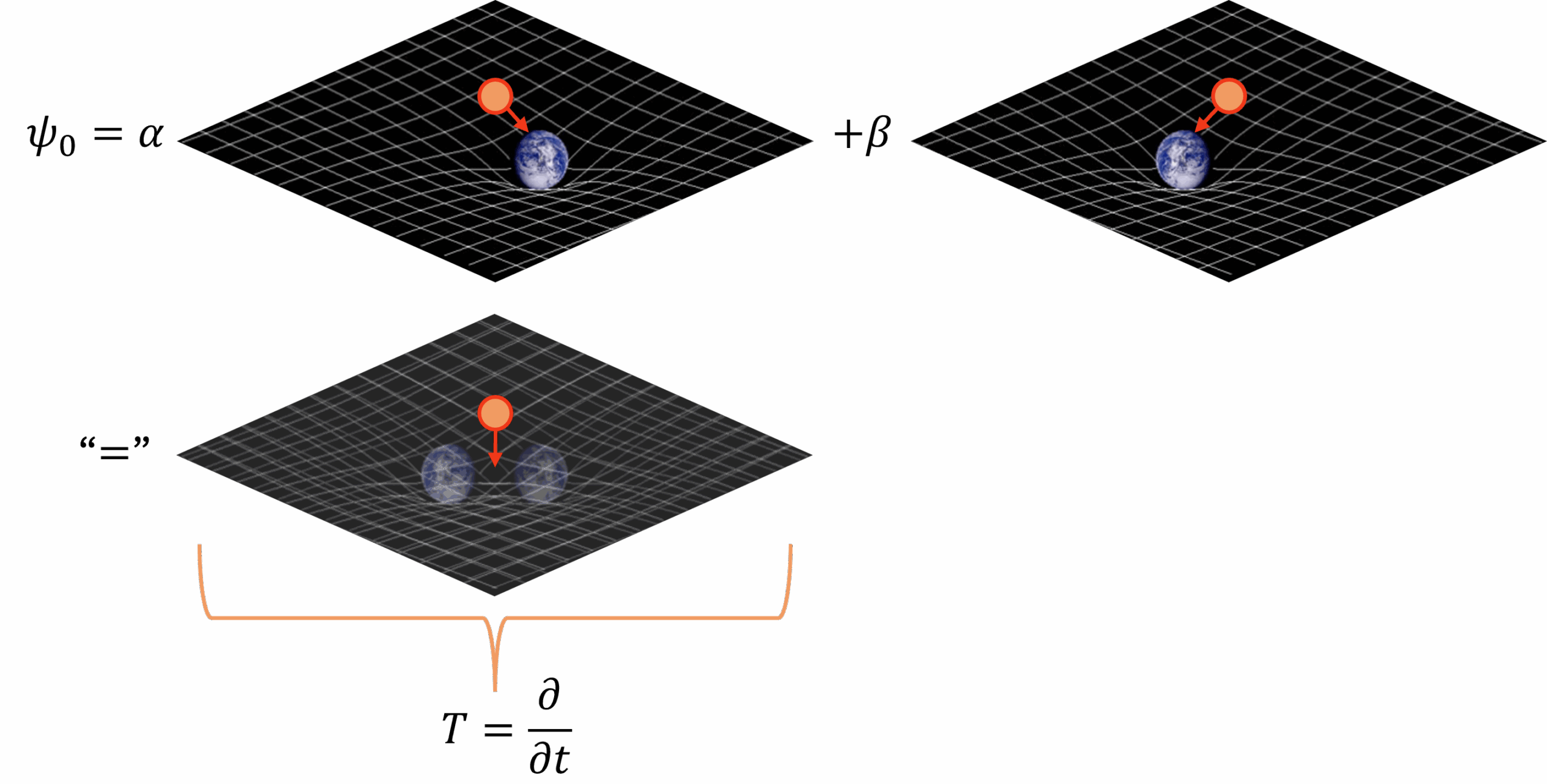
Het probleem is echter dat in de onderste afbeelding de twee aardes grof gezegd allebei een beetje aanwezig zijn in één ruimtetijd, met een gewicht gegeven door \( \alpha \) en \( \beta \). Als twee zware objecten echter dicht bij elkaar zijn in één ruimtetijd, zullen ze elkaar aantrekken en naar elkaar toe bewegen, zoals elke zwaartekrachtstheorie voorspelt. Het onderste plaatje in afbeelding 5 komt dus niet overeen met een stabiele toestand in de algemene relativiteitstheorie, terwijl de superpositie in het bovenste plaatje wél stabiel is volgens de quantummechanica. De ruimtetijdstapeling van afbeelding 5 lost het probleem om één tijd te definiëren die consistent is met de quantummechanica én de algemene relativiteitstheorie dus niet op!

Om deze reden stelt Penrose dat er een conflict bestaat tussen de principes van de quantummechanica en die van de algemene relativiteitstheorie: we kunnen de tijdsevolutie van een superpositie van twee ruimtetijden niet beschrijven op een manier die consistent is met zowel quantumtheorie als algemene relativiteitstheorie. Mij nodigt het conflict tussen twee fundamentele theorieën van ons universum uit om eens goed na te denken over wat we precies bedoelen met een theorie van quantumzwaartekracht!

[1] Een belangrijke subtiliteit die ik in dit artikel niet uitgebreid behandel, is dat in de algemene relativiteitstheorie coördinaattransformaties de fysica niet mogen veranderen: welke coördinaten je ook gebruikt, je zou dezelfde natuurkundige fenomenen moeten beschrijven. De twee gesuperponeerde toestanden in afbeelding 3 zijn gerelateerd door een coördinaattransformatie en zouden in de algemene relativiteitstheorie dus als dezelfde toestand worden beschouwd. Het is echter mogelijk om de twee toestanden daadwerkelijk verschillend te maken door verdere objecten in de omgeving te beschouwen. Penrose doet dit zorgvuldig in zijn artikel.