
Waterstof is het meest voorkomende element in ons universum. Het bestaat simpelweg1 uit een enkel proton dat de atoomkern vormt en een elektron dat daaromheen beweegt. Klassiek gezien hebben we het beeld van een elektron dat rondom de kern draait zoals de aarde dat rondom de zon doet, maar in werkelijkheid is de situatie veel ingewikkelder: het elektron moet je eigenlijk zien als soort wolk die rondom het proton hangt. De vorm en dichtheid van die wolk wordt precies beschreven door de quantummechanische golffunctie, die een oplossing is van de beroemde Schrödingervergelijking.
Laten we beginnen met het formuleren van deze vergelijking, die er als volgt uitziet2:
\( -\frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2}+V(x)\Psi = E \Psi \),
Hierin zien we de ruimtecoördinaat \( x \), de gereduceerde constante van Planck \( \hbar \), de massa \( m \) van het elektron, de energie \( E \) van het elektron en de golffunctie \( \Psi \) die de dichtheid van de ‘elektronwolk’ beschrijft. Verder hebben we de potentiaal \( V(x) \), de plaats-afhankelijke potentiële energie van het elektron, en zien we aan de linkerzijde de tweevoudige afgeleide van de golffunctie met betrekking tot de plaats \( x \), wat je zou kunnen interpreteren als een kracht die aan de golffunctie trekt.
In de vergelijking hierboven staat maar één plaatscoördinaat, \( x \), maar het waterstofatoom willen we eigenlijk in drie dimensies \( (x, y, z) \) beschrijven, wat het probleem een stuk lastiger maakt. We kunnen echter gebruikmaken van het feit dat het waterstofatoom symmetrisch is onder rotaties: net als een biljartbal ziet de kern van het waterstofatoom – simpelweg een proton – er vanuit iedere hoek hetzelfde uit. Wat dan volgt is een lange wiskundige berekening die ik hier niet zal toelichten, maar de conclusie van dat verhaal is dat we ons driedimensionale probleem uiteindelijk kunnen reduceren tot de volgende ééndimensionale Schrödingervergelijking:
\( -\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial r^2} + \left(- \frac{e^2}{4\pi \epsilon_0} \frac{1}{r}+\frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right)u = E u \).
De variabele \( r \) is hier de afstand tussen het proton en elektron – de enige richting die nog een rol speelt – en de functie \( u(r) \) waarvoor we de vergelijking willen oplossen is de zogenoemde radiële component van de golffunctie \( \Psi \) waarin we geïnteresseerd zijn. Tussen de haakjes zien we nu twee uitdrukkingen staan: de eerste is de zogeheten Coulombpotentiaal die de aantrekkende kracht tussen het elektron en proton beschrijft. Die term bevat de elementaire lading \( e \) en de elektrische veldconstante \( \epsilon_0 \). De tweede term is een soort centrifugaalkracht die het deeltje naar buiten wil slingeren3. Die term is een gevolg van de technische berekening die ik ook achterwege laat; merk wel op dat die term afhangt van een getal \( l \) dat de verschillende oplossingen labelt.
De potentiaal waarin het elektron zich bevindt ziet er schematisch als volgt uit:
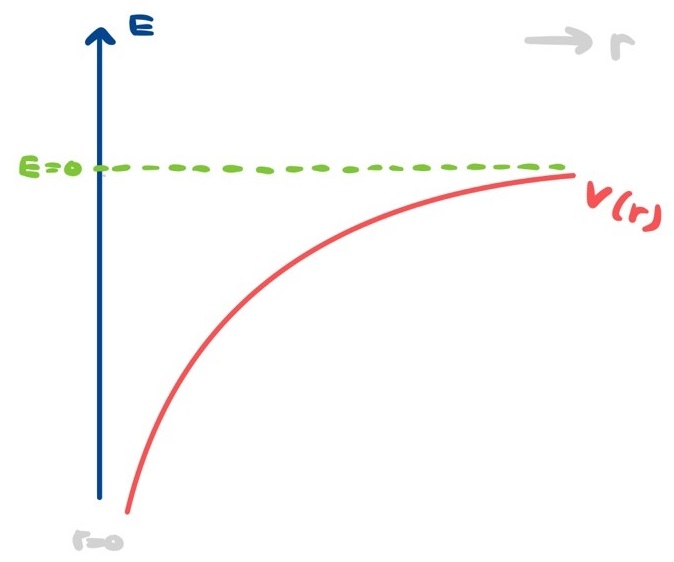
Als het elektron zich oneindig ver van het proton bevindt, heeft het een potentiële energie van nul, maar naarmate het dichterbij komt neemt die energie af (en wordt dus negatief) wat betekent dat er energie vrijkomt. Klassiek gezien zou je kunnen redeneren dat het elektron daardoor alsmaar dichterbij komt en uiteindelijk op het proton knalt. Quantummechanisch is dit niet wat er gebeurt. De bovenstaande vergelijking kan opgelost worden en leidt niet alleen tot een precieze uitdrukking voor \( u(r) \) en dus voor de golffunctie \( \Psi \), maar geeft daarmee ook de mogelijke energieën van het elektron. Het blijkt dat die, net zoals bij de harmonische oscillator, een discrete verzameling vormen die we kunnen labelen met een positief geheel getal \( n \) en die de volgende waarden aannemen:
\( E_n = -\frac{m}{2\hbar^2}\left(\frac{e^2}{4\pi \epsilon_0}\right)^2 \frac{1}{n^2} \).
Als we de numerieke waarden van de constanten hierboven invullen vinden we
\( E_n = \frac{-13{,}6 \text{ eV}}{n^2} \).
Wat we dus zien is dat, als een elektron van grote afstand met potentiële energie \( E=0 \) zich laat binden aan het waterstofatoom en daarbij afzakt naar de grondtoestand \( n=1 \), er 13,6 elektronVolt aan energie vrijkomt. Verder dan dat kan het deeltje niet zakken! Er bestaat dus, in tegenstelling tot wat je klassiek zou verwachten, een kleinst mogelijke baan voor het elektron. De energie die vrijkomt in het hierboven beschreven proces noemen we ook wel de bindingsenergie van het elektron aan het proton. Omgekeerd betekent dit ook dat je, als je het elektron van het proton wil losmaken, minstens 13,6 eV aan energie in het atoom moet stoppen. De makkelijkste manier om dat te doen is door een foton met een energie van ten minste 13,6 eV op het waterstofatoom te schieten en zo het elektron als een biljartbal weg te kaatsen. Dit proces noemt men ook wel ionisatie, aangezien het eenzame proton dat overblijft een positief geladen ion is. Als je een foton met minder dan 13,6 eV op het atoom afvuurt, zul je het elektron niet kunnen losmaken, maar het mogelijk wel in een hogere energietoestand – een hoger gelegen baan – kunnen brengen.
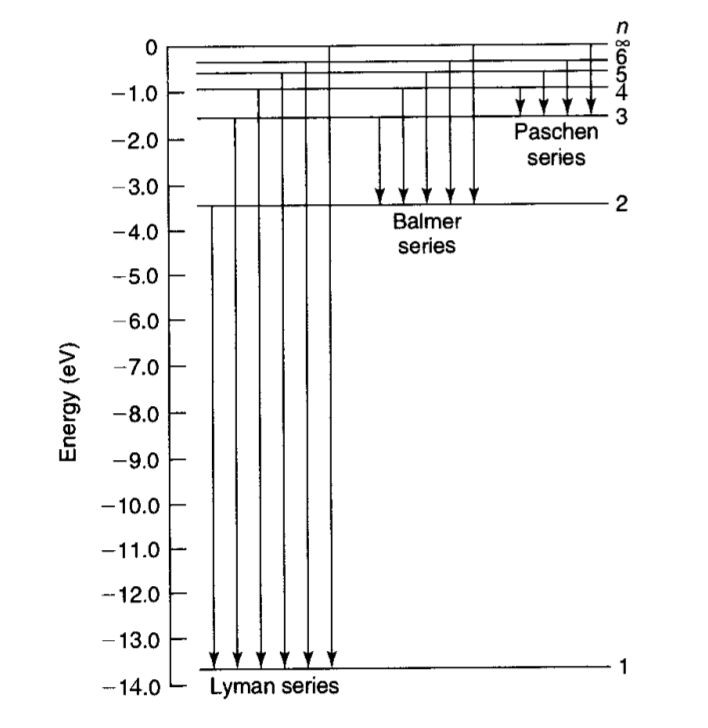
Om het elektron van een toestand met label \( n \) naar een toestand met label \( m \) te brengen, heb je
\( E_m-E_n = -13{,}6 \text{ eV }\times \left(\frac{1}{m^2}-\frac{1}{n^2}\right) \)
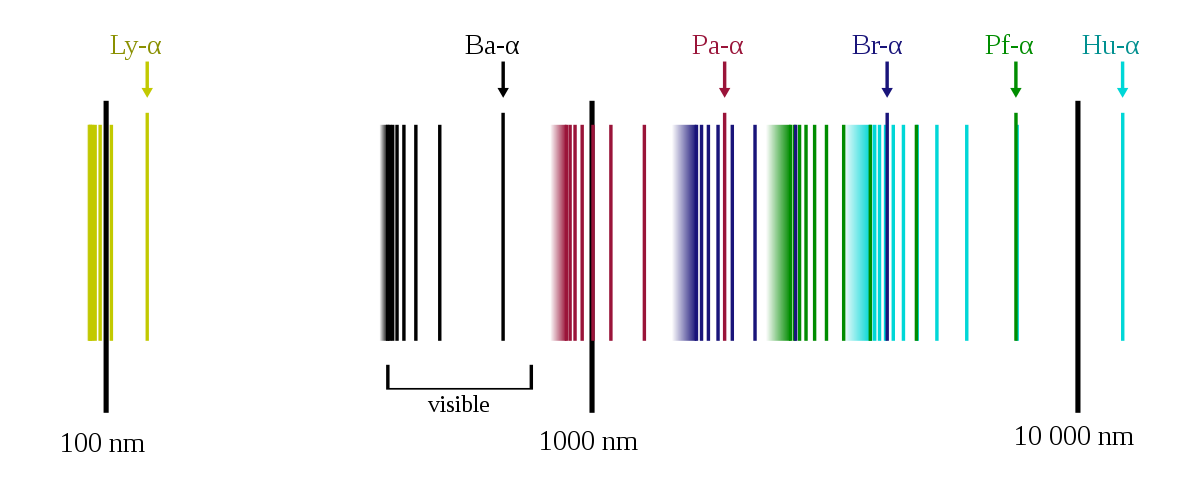
aan energie nodig. Zoals besproken in mijn eerdere artikel produceert een elektron dat naar een lagere energietoestand springt omgekeerd fotonen waarvan de energie precies berekend kan worden met de bovenstaande formule. Dit leidt tot de beroemde spectraallijnen van waterstof die in de afbeelding hieronder zijn afgebeeld. De verschillende reeksen corresponderen met sprongen vanuit hoger gelegen toestanden (zie de afbeelding hierboven) naar bijvoorbeeld de \( n=1 \)-toestand (Lyman) of de \( n=2 \)-toestand (Balmer), enzovoort. De golflengte \( \lambda \) van het foton dat bij deze sprongen ontstaat – en dus: van het licht dat je kunt waarnemen – kun je berekenen met de formule
\( \lambda=\frac{\hbar c}{E} \).
waarin \( c \) de snelheid van het licht is. In het laboratorium kunnen we ook exact al deze golflengtes waarnemen, en ze blijken heel nauwkeurig met de berekeningen te kloppen. Een mooie triomf voor de quantummechanica!
Er zijn in de natuurkunde maar heel weinig modellen die én exact oplosbaar én echt fysisch zijn, in de zin dat je ze ook echt in de natuur kunt vinden en kunt beproeven. Het waterstofatoom is een van deze modellen. De quantumbeschrijving van het waterstofatoom is dan ook een standaard-probleem dat iedere natuurkundige eenmaal in zijn leven moet hebben bestudeerd!
[1] We gaan hier uit van de meest voorkomende isotoop van waterstof: \( H_1^1 \). Deuterium (\( H_1^2 \)) en tritium (\( H_1^3 \)) laten we dus buiten beschouwing.
[2] Dit is de tijdonafhankelijke Schödingervergelijking. Als je deze vergelijking oplost kun je echter op eenvoudige wijze de oplossing van de algemene (tijdafhankelijke) Schrödingervergelijking produceren.
[3] Naarmate je dichter bij het atoom komt wordt \( r \) kleiner en \( r^{-2} \) dus steeds groter. Dit moet gecompenseerd worden in deze vergelijking door de versnelling \( \frac{\partial^2 u}{\partial r^2} \) ook heel groot te maken, wat tot gevolg heeft dat het deeltje naar buiten gedrukt wordt.