
In this series of articles we will explore some approaches to describe gravity on a quantum scale and unravel the triumphs and failures of these. For that I first state the main conceptual problems that arise when merging quantum theory and Einstein’s theory of general relativity.
Then in the next episodes we will take a deep dive into these explicit attempts, which encompass string theory, loop quantum gravity and many more.
Black hole information paradox
Black holes are the universe’s sinks, as they have the property that nothing, not even something moving at the speed of light, can escape them. From Einstein’s theory of general relativity we know that they are entirely characterized by three quantities: their mass, charge and state of rotation. An important property of black holes is their entropy, roughly defined as the uncertainty of describing a system’s exact microscopic state. Perhaps we would expect, from general relativity i.e. these three numbers, that the black hole entropy \( S=0 \) as there is no uncertainty about the black hole’s exact state.
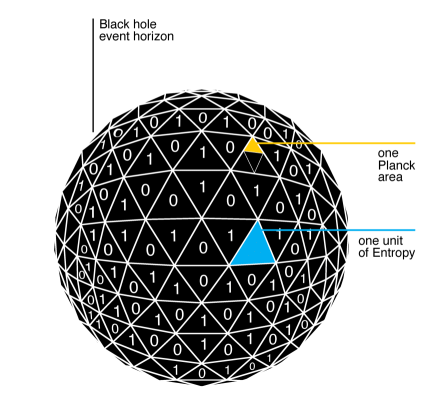
This all changed when Stephen Hawking showed that black holes, when looked at from a quantum point of view, radiate and have an entropy
\( S=\frac{A}{4A_p} \),
where \(A\) is the surface area of the black hole and \(A_p\) is the Planck area. The Planck area is expected to be the fundamental area unit of spacetime of order \(10^{-70} m^2\), which is a very small number. The fact that Hawking found the entropy of black holes to be nonzero leads us to a contradiction with the description provided by general relativity.
Even more unexpected was the fact that this Hawking radiation (at a fixed black hole temperature) always looks the same, no matter what the black hole was made out of in the first place. A CD with a copy of The Black Eyed Peas’ song Where Is The Love? would result in the same Hawking radiation as a hot espresso. All the information about the song’s profound lyrics, the musician’s passionate singing and the harmonious symphony of the strings, violins and drums does not matter when it comes to the radiation escaping the black hole. All Hawking radiation is the same. The process of something falling into the black hole and escaping through Hawking radiation is, therefore, an information-erasing process. That may not bother you when you first hear it, but the problem is: this is not allowed by the fundamental laws of quantum mechanics! We need our theories to not lose information as otherwise we would not be able to predict/post-dict physical properties!
This brings us to the main puzzles:
Question 1: How can we restore the information about the stuff that falls into the black hole after the Hawking radiation has come out?
Question 2: Where does the entropy of black holes come from?
The problem of time
The problem of time lies at the conceptual heart of both quantum mechanics and general relativity. The issue is that we treat time very differently in both theories.

In quantum mechanics, a system, for instance the motion of an electron around a nucleus, changes in time following the Schrödinger equation. This equation dictates that the dynamics, meaning the time evolution, of a given system is described by the energy (‘hamiltonian’) of that system. Here “time” is an absolute number that is the same in the entire universe, not only in a subsystem like an atom. Everybody ‘uses the same clock’.
This is fundamentally different from how we interpret time in general relativity. In relativity we no longer have an absolute notion of time, as time is now part of spacetime. Spacetime is the dynamical fabric of our universe, which can bend and curve depending on the matter in any given region. But now, depending on that matter, we find that time will bend and curve as well, thereby resulting in a relative notion of time: different observers must use different clocks.
How does this problem show up in calculation? Well, if we want to find the quantum hamiltonian for general relativity, by naively using the common rules for quantization, we find that the ‘Schrödinger equation’[1] reads
\( \hat{H}\psi=0 \),
which tells you that the system, meaning the content of the universe, is not changing in time. Hence, nothing ever happens in our universe! That seems rather odd.
Therefore, we find the main puzzle to be:
Question 3: How do we incorporate time (spacetime) into a purely quantum-mechanical description?
Other issues and outline
Of course there are more issues concerning the description of a quantized gravitational field, as for instance the non-renormalizability of Einstein gravity and the fact that one finds spacetimes, from Einstein’s equations, which host unphysical singularities.
The ultimate goal of this series is to present the current approaches that physicists have come up with for circumventing some of these issues and to illustrate where these approaches triumph and where they fail. So, join us in the journey through quantum spacetime!
[1] This equation is known as the Wheeler-DeWitt equation.