
Een bol, een berg en een balans
Voor wie Jeremy’s artikel destijds niet gelezen heeft, eerst nog maar even een herinnering. Hoe hebben we de massa van de Aarde ooit bepaald? Tot grofweg 1770 was het beste antwoord op die vraag: schatten. Want hoewel men voor die tijd niet goed wist hoe zwaar de Aarde was, was al wel vrij goed bekend hoe groot de Aarde was. De oude Grieken hadden al door dat de Aarde een bol moest zijn: als je ver reist, staan om middernacht heel andere sterren recht boven je hoofd dan op de plek waar je vandaan kwam. Uit die “verschuiving” van de sterrenhemel kun je de omtrek van de Aarde bepalen, en het lukte Eratosthenes al zo’n twee eeuwen voor het begin van onze jaartelling om daaruit de omtrek van de Aarde tot op een paar procent nauwkeurig te meten. Hoewel er sindsdien (en zelfs vandaag de dag nog) de nodige mensen aan de bolvorm van de Aarde hebben getwijfeld, weten we inmiddels nog veel nauwkeuriger wat de omtrek van onze aardbol is: vrijwel precies 40.000 kilometer.
Dat “vrijwel precies” hangt natuurlijk af van wáár je die omtrek meet, want de Aarde is geen perfecte bol. Doordat de Aarde draait is de evenaar – door de centrifugale krachten – een klein beetje ‘opgerekt’, en ook getijden en bergketens zorgen voor een omtrek die op verschillende plaatsen en tijdstippen steeds net iets anders is. Een van de eerste definities van de meter, als 1/10.000.000e deel van de afstand van de evenaar tot de Noordpool, gemeten over de meridiaan die door Greenwich loopt, is dan ook niet heel nauwkeurig – of omgekeerd: de exacte omtrek van de Aarde is vrijwel nergens en nooit exact 40.000 kilometer. Als we niet té veel decimalen achter de komma willen weten is die grootte, en de benadering dat de Aarde een perfecte bol is, toch een heel behoorlijke aanname.
Een kleine terzijde: je kunt je natuurlijk afvragen of we de atmosfeer van de Aarde niet ook in onze berekeningen moeten meenemen. Nu is die atmosfeer qua dikte vergelijkbaar met de schil van een appel – afhankelijk van waar je de grens legt enkele tientallen kilometers dik – en bestaat de atmosfeer natuurlijk uit betrekkelijk licht gas, dus binnen de nauwkeurigheid waarmee we nu werken kunnen we de atmosfeer zonder problemen verwaarlozen. De atmosfeer zorgt er zelfs voor dat de massa van de Aarde in de loop van de tijd verandert: er “verdampt” jaarlijks zo’n 100 miljoen kilogram van de atmosfeer die onze planeet in de ruimte achterlaat. Ten opzichte van de hele atmosfeer (zo’n 5 x 1018 kilogram) is ook dát weer verwaarloosbaar – zeker omdat het voor ongeveer de helft gecompenseerd wordt door meteorieten en ander ruimtestof dat weer óp de Aarde terechtkomt.
Terug naar de grootte van de Aarde. Wie de omtrek van de aardbol weet, kan met de formule voor een cirkel ook de straal uitrekenen – daar komt zo’n 6.366 kilometer uit, een waarde die heel mooi ligt tussen de inmiddels bekende “echte” straal bij de polen (6.357 kilometer) en bij de evenaar (6.378 kilometer). Vervolgens kunnen we ook het volume van de aardbol uitrekenen: met de bekende bolformules komt daar 1,081 x 1021 kubieke meter uit. Ook die waarde ligt weer mooi dicht bij het tegenwoordig nauwkeuriger bepaalde echte antwoord: 1,083 x 1021 kubieke meter.
So far, so good – het volume van de Aarde kunnen we dus al eeuwenlang behoorlijk nauwkeurig uitrekenen. Als we nu ook de dichtheid van de Aarde zouden weten, konden we ook de massa van onze planeet bepalen – massa is immers dichtheid maal volume. Maar hoe groot is die dichtheid? Van water weten we dat 1 liter vrijwel precies 1 kilogram weegt, en 1 kubieke meter (1000 liter) dus zo’n 1000 kilogram. Maar gesteente is zwaarder: de meeste steensoorten zijn zo’n anderhalf tot drie keer zo zwaar als water. Metalen zijn nog zwaarder: een kubieke meter ijzer weegt bijvoorbeeld al bijna 8000 kilogram. Natuurlijk kon men in het verleden nog niet goed in het binnenste van de Aarde kijken – eigenlijk kunnen we dat nog steeds niet – maar de schattingen van de massa van onze planeet kwamen dus allemaal uit op “enkele malen 1024 kilogram”. Tussen de verschillende waarden waar men op uit kwam kon echter zomaar een factor twee of drie zitten.

Zoals in Jeremy’s artikel beschreven waren er twee metingen die die nauwkeurigheid flink wisten te verbeteren. Allereerst was er in 1774 de meting onder leiding van Nevil Maskelyne en Charles Mason die in de buurt van de Schotse berg Schiehallion probeerden te bepalen hoe sterk de massa van die berg de loodlijn van een slinger naar het middelpunt van de aarde veranderde. Alle zwaartekracht trekt immers aan zo’n slinger: de gladde aardbol zou de slinger perfect omlaag trekken, maar de aanwezigheid van een flinke berg náást de slinger trekt de slinger ook een klein beetje opzij. Door als het ware heel nauwkeurig langs een slinger naar de sterrenhemel te kijken, en dat aan twee kanten van de berg te doen, kon astronoom Mason meten dat de berg een heel klein beetje aan de slinger trok, en op basis daarvan kon hij weer bepalen wat de verhouding was tussen de dichtheid van de berg en de dichtheid van de aardbol. Het eindresultaat was dat de aardbol ongeveer 4,5 keer de dichtheid van water moest hebben, en dat de Aarde dus zo’n 4,5 x 1024 kilogram moest wegen.
Nog veel nauwkeuriger was de meting van Henry Cavendish, zo’n 25 jaar later, in 1798. Cavendish probeerde niet de dichtheid van de Aarde te meten, maar nam enkele loden bollen, waarvan hij de dichtheid en massa heel precies wist, en probeerde de zwaartekracht te meten die die bollen op kleinere, dichtbijzijnde massa’s uitoefenden. Dat klinkt volkomen ondoenbaar – vergeleken met de zwaartekracht van de hele Aarde zijn die krachten extreem klein – maar door de kleinere massa’s heen en weer te laten bewegen aan een zogeheten torsiebalans (in feite niet meer dan een verticaal draadje waaraan een horizontaal stokje bevestigd zit dat kan draaien) en vervolgens de loden bollen van de ene naar de andere kant te verplaatsen, kon Cavendish toch nauwkeurig meten dat de kleine massa’s rond nét een ander evenwichtspunt gingen slingeren, en zo kon hij de zwaartekracht van de loden bollen meten. Die vergeleek hij met de zwaartekracht van de Aarde – die natuurlijk veel makkelijker te meten is – en zo kon hij de massa van de loden bollen vergelijken met die van de Aarde. Cavendish’ antwoord voor de aardmassa was zo’n 5,9 x 1024 kilogram – een waarde die maar weinig afwijkt van de tegenwoordig preciezer bekende waarde van 5,972 x 1024 kilogram.
De omgekeerde wereld
Terug naar onze vraag: waarom willen we eigenlijk graag weten hoe zwaar de Aarde is? Natuurlijk is het een interessant feitje op zichzelf, wat tijdens de juiste pubquiz misschien wat punten oplevert, maar het weten van de massa van de Aarde is ook van wetenschappelijk belang. Twee belangrijke redenen daarvoor kunnen we achterhalen als we de redenering achter de experimenten hierboven simpelweg omdraaien.
Wat Maskelyne en Mason bijvoorbeeld eigenlijk bepaalden was de dichtheid van de Aarde – volgens hun meting zo’n 4,5 maal die van water; volgens wat we nu preciezer weten zelfs zo’n 6 maal die van water. Als je die dichtheid bepaald hebt, kun je ook een inschatting maken van waar de Aarde van binnen uit bestaat – niet uit water, dus, maar dus ook niet uit alleen maar gesteente: dan zou de dichtheid veel lager zijn. De meting van Maskelyne en Mason was dus de eerste die erop wees dat het binnenste van onze Aarde van metaal moest zijn – met ijzer als eigenlijk enige realistische kandidaat. Tegenwoordig weten we dat de Aarde inderdaad een grote kern van vloeibaar ijzer bevat. Met die kennis kunnen we weer dingen leren over de magneetvelden op Aarde, over hoe de aardbol in de loop van de (miljoenen) jaren langzaam is afgekoeld en in de verre toekomst nog verder zal afkoelen, enzovoort.
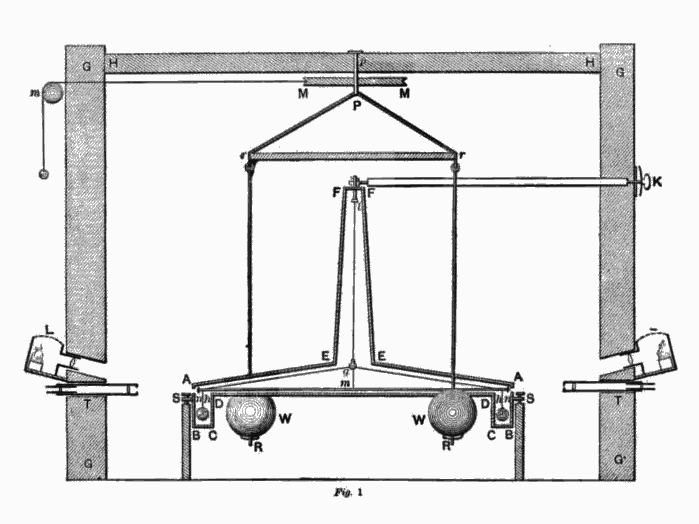
Uit het experiment van Cavendish leerden we juist hoe sterk de zwaartekracht is; in feite bepaalde Cavendish de zogeheten zwaartekrachtsconstante van Newton, een universele contstante die voorkomt in de door Isaac Newton opgeschreven natuurwet die vertelt hoe sterk de zwaartekracht tussen twee willekeurige massa’s is. “Universeel” is daarbij het belangrijke woord: toen we Newtons constante eenmaal goed hadden bepaald, konden we ook de zwaartekracht tussen andere sterren, planeten en zelfs hele sterrenstelsels bepalen, en zo van alles leren over de evolutie van ons heelal. Natuurlijk paste Einstein later Newtons wetten nog aan, maar ook in Einsteins beschrijving van de zwaartekracht komt de constante van Newton voor. En de grote moderne kosmische raadsels – wat is donkere materie, bijvoorbeeld, of wat gebeurt er binnen in een zwart gat – hebben allemaal te maken met de zwaartekracht, en hebben zowel voor hun formulering als voor het vinden van een mogelijke oplossing een nauwkeurige kennis van de sterkte van die zwaartekracht nodig.
Dáárom wilden al die wetenschappers uit het verleden dus uiteindelijk graag weten hoe zwaar de aarde is. Door het bestuderen van een berg of een loden bol leren we uiteindelijk van alles over onze hele planeet, en daarmee zelfs over wat er gebeurt in de verste uithoeken van ons heelal!