
Figure 1. A floating superconductor.Superconductivity is one example of what can happen when things get quantum critical. Image: US Department of Energy.
One of the main goals of physics is to understand how matter transforms when its environment changes. For example, why does liquid water turn into ice when it’s cold enough? Liquid water and ice are two different phases of water molecules, and the change from one to the other is called a phase transition. Phase transitions are currently at the centre of one of the longest standing mysteries in quantum physics: the relationship between quantum phase transitions and exotic behaviour like superconductivity.
One of the most common types of change between states of matter is the transition between an ordered phase and a disordered phase. For example, the transition between a liquid and a solid: upon cooling, the molecules or atoms that in a liquid move freely in a disordered fashion, will arrange themselves into (approximately) fixed positions and form a solid, where these molecules or atoms are ordered.
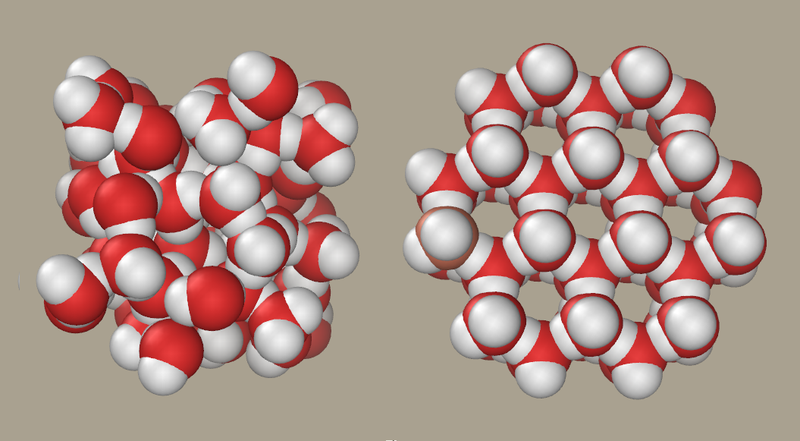
Figure 2. Water and ice.In ice (right), water molecules are ordered; in liquid water (left), they are not. Image: P99am.
A matter of scale
Interestingly, when a system is close to being ordered, it already looks like it is ordered at a small scale. That is, if one looks only at a small region, this region might look ordered. However, when one looks at a larger region of this system, i.e. a region of larger length scale, it will still look disordered because the various small regions are not all ordered in the same way. The closer one gets to the phase transition, the larger the scale at which the system looks ordered. At the phase transition, this scale formally extends to infinity, and the system looks ordered at all scales.
This is the central idea of the mathematical framework of “renormalisation”, the discovery of which won Kenneth G. Wilson the Nobel prize in 1982. Mathematically, we can describe a physical system in terms of the interactions between its relevant components, be it elementary particles, atoms, molecules, or (at larger scales) groups of these. Very close to a phase transition, the system looks the same on a small and a large scale, which means that the mathematical description of the system at these two different length scales should equal one another. Writing this idea down in formulas gives us a “renormalisation equation”, which we can then solve. This then gives predictions for how the system behaves close to the transition, which can be tested against experimental data.
Video: The renormalisation group.Near a phase transition, a system becomes scale independent.
One striking feature of this renormalisation theory is that, being based on scale invariance, it does not depend on details of the system and is therefore “universal”. Many different physical systems have the same behaviour close to a phase transition. This allows us to group them together in different categories called “universality classes” and understand better how they are related.
From thermal to quantum
Almost all phase transitions we know from everyday life are driven by temperature or, more precisely, by thermal fluctuations. The higher the temperature, the more energy small particles have to move around, which means they can overcome the tendency to order. In the example of ice melting, at high enough temperature the water molecules have enough kinetic (or equivalently thermal) energy to break the bonds holding them together.

Figure 3. Ice melting is an example of a thermal phase transitionImage: Pikrepo.com
Curiously, there are phase transitions that occur at zero temperature (by changing another parameter, such as pressure). These transitions cannot be driven by thermal energy, because at zero Kelvin the thermal energy is zero. Instead, these transitions are called quantum phase transitions because they are driven by quantum-mechanical fluctuations, which in turn stem from Werner Heisenberg’s uncertainty principle. The zero-temperature transition point is called a quantum critical point.
Fortunately, we can apply renormalisation theory to both thermal and quantum phase transitions given that in both cases the system exhibits a scale invariance close to the transition. Renormalisation theory is expected to (only) describe what happens close to the transition temperature. However, quantum phase transitions behave as predicted by this theory up to temperatures more than a hundred degrees above absolute zero! This means that the presence of a quantum critical point has a much bigger effect on the behaviour of a material than being close to a thermal phase transition would. It is therefore very interesting to study quantum phase transitions in particular.
A key to superconductivity?
Quantum phase transitions modify the properties of a material so much that it has been thought to be responsible for superconductivity in some cases. In particular, some types of materials consistently become superconducting in the region of parameter space surrounding a quantum critical point. Physicists have already managed to develop simplified models which show the same behaviour. The next step is to understand whether the ideas introduced in these simple models can be used to explain the results of experiments performed on real materials. This would bring us one step closer to understanding these fascinating quantum critical systems.