Heb je wel eens goed opgelet als je in je kopje thee roert? Wat denk je dat er gebeurt met kleine theeblaadjes op de bodem? Je zou misschien verwachten dat de blaadjes door de cirkelbeweging en een resulterende centrifugale kracht naar buiten worden geduwd – net zoals stoeltjes in een zweefmolen. Dat die intuïtie niet klopt, kan een simpel experiment aan de keukentafel uitwijzen: de theeblaadjes hopen zich op in het midden van het kopje. Het was Einstein die hiervoor in 1926 de theoretische verklaring bood – dus grofweg tien jaar nadat hij een radicaal nieuwe theorie over de zwaartekracht had ontwikkeld. Blijkbaar was de zogeheten tea leaf paradox een onverwacht ingewikkeld probleem.

Afbeelding 1. Theeblaadjes in een theekopje.Foto: Wikipedia-gebruiker Apoc2400.
Einstein realiseerde zich dat het theekopjesprobleem gerelateerd was aan de vraag waarom rivieren meanderen, en schreef daar een artikel over: “The Cause of the Formation of Meanders in the Courses of Rivers and of the So-Called Baer’s Law”. Het artikel bevat geen enkele vergelijking, en slechts drie plaatjes – en daarvan zijn er twee van een theekopje. Een benadering die kenmerkend is voor een natuurkundige die vooral op gedachte-experimenten bouwde. Laten we de redenering van Einstein eens nalopen.
De theeblaadjes op de bodem van een kopje blijven daar liggen omdat ze zwaarder zijn dan het theewater. Als we nu het water laten ronddraaien, bijvoorbeeld met een lepeltje, veroorzaakt dat een centrifugale kracht op de vloeistof. In de buurt van de wand van het kopje ondervindt de vloeistof een beetje wrijving, waardoor de rotatiesnelheid daar lager is dan in het midden. Als een gevolg hiervan is de centrifugale kracht in de buurt van de bodem lager dan hoger in het kopje. De vloeistof bovenin het kopje heeft dus méér de neiging om naar buiten te gaan dan de vloeistof onderin. De vloeistof die bovenin naar buiten toe stroomt, moet natuurlijk ook ergens blijven, en het eindresultaat blijkt te zijn dat er een andere, verticale cirkelbeweging ontstaat, zoals in afbeelding 2 – de zogeheten secundaire cirkelbeweging. Door deze ‘secundaire cirkelbeweging’ worden de theeblaadjes naar het midden geveegd en blijven daar liggen.
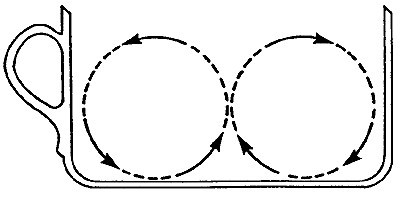
Afbeelding 2. De secundaire cirkelbeweging.Afbeelding uit Einsteins artikel.
Hoe zit dat dan met meanderende rivieren? Hier gebeurt iets soortgelijks. Laten we voor het gemak eerst aannemen dat er al een bocht in de rivier is. In zo’n bocht ontstaat een centrifugale kracht in de richting van de buitenkant van de kromming (van A naar B in afbeelding 3). Deze kracht is op de bodem kleiner dan minder diep in de rivier, waardoor weer een secundaire cirkelbeweging ontstaat (de rechter schets in afbeelding 3). Het water bovenin deze curve gaat sneller dan onderin, en daarom is de erosie aan de rechterkant (waar het water van boven aankomt) sterker.
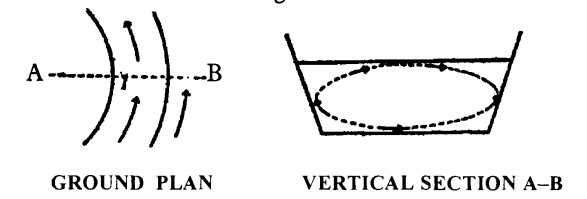
Afbeelding 3. De cirkelbewegingen in een rivier.Links de beweging die ontstaat ten gevolge van de bocht, van bovenaf gezien; rechts de secundaire cirkelbeweging, van opzij gezien. Afbeelding uit Einsteins artikel.
Als er nog geen bocht in de rivier is, kan theoretisch toch een soortgelijk effect optreden: ditmaal is het geen lepeltje die de vloeistof doet ronddraaien, maar de draaiing van de aarde. Die veroorzaakt ook een heel kleine centrifugale kracht, waarvan de richting afhangt van de breedtegraad waar de rivier zich bevindt. Dit betekent dat de erosie in het noordelijk halfrond door dit effect groter is aan de rechterkant van de rivier, en in het zuidelijk halfrond aan de linkerkant van de rivier. Dit effect – Baer’s law, waarover Einstein het in zijn titel heeft – is echter heel klein; in de praktijk zijn er vrijwel altijd andere factoren die het meanderpatroon van een rivier sterker beïnvloeden. Als de bocht er eenmaal is, speelt het theeblaadjes-effect echter een belangrijke rol.
De praktische toepasbaarheid van Einsteins theoretische beschrijving van het theeblaadjes-effect is wellicht wat directer dan die van zijn algemene relativiteitstheorie. Rivieren en theekopjes zijn namelijk niet de enige gevallen waarin deze kennis van belang is: ook het begrijpen van druksystemen in de atmosfeer berust hierop, het proces van bierbrouwen, en een nieuwe techniek om rode bloedcellen van bloedplasma te scheiden. Leuk om aan te denken, als je een volgende keer naar de blaadjes in je theekopje staart.