Entropie (2): Een eenvoudig voorbeeld

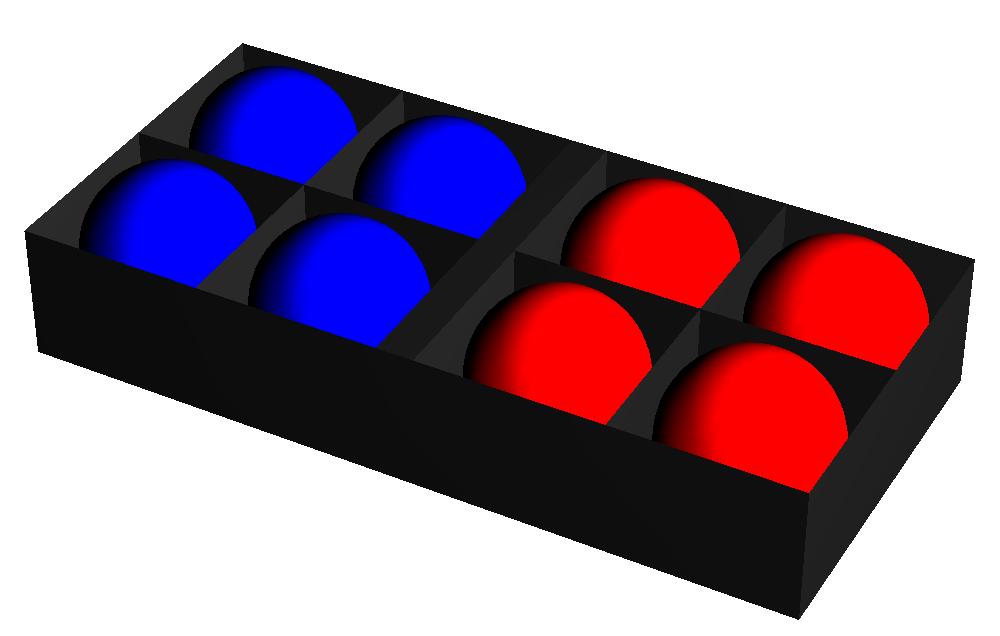
Afbeelding 1. Een gesorteerde ballenbak

Wanneer we haast hebben bij het opruimen zal de kleurschikking ons echter niet veel interesseren, en zullen de ballen willekeurig over de compartimenten verdeeld worden – bijvoorbeeld zoals in afbeelding 2. In dit voorbeeld hebben we aan beide kanten twee blauwe ballen en twee rode.

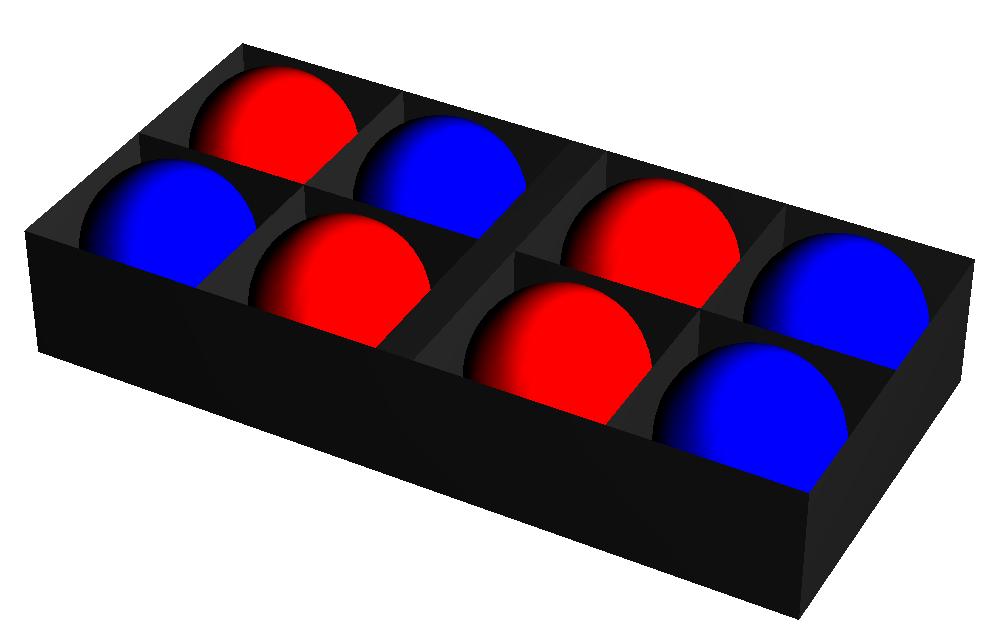
Afbeelding 2. Een ongesorteerde ballenbak

We kunnen ons nu het volgende afvragen. Als we de ballen volkomen willekeurig opbergen, welke uitkomst is dan waarschijnlijker – de geordende in afbeelding 1, of de chaotische in afbeelding 2? Het antwoord op die vraag hangt af van wat we precies bedoelen met “de chaotische uitkomst in afbeelding 2”. Laten we vraag eerst in de meest letterlijke zin interpreteren:

Welke uitkomst is waarschijnlijker:

(1A) de exacte situatie zoals in afbeelding 1, of
(1B) de exacte situatie zoals in afbeelding 2?

Het antwoord is: beide uitkomsten zijn precies even waarschijnlijk. In beide gevallen gaat het om een situatie waarin we de rode ballen in vier vooraf gekozen compartimenten terugvinden, en de blauwe ballen in de andere vier compartimenten. Dat in afbeelding 1 die vier compartimenten toevallig naast elkaar liggen en in afbeelding 2 niet, maakt voor de waarschijnlijkheid van de uitkomst niet uit.

Afbeelding 3. Een andere ongesorteerde configuratie

Wie dit antwoord verrassend vindt, had waarschijnlijk een net iets andere vraag in gedachten:

Welke uitkomst is waarschijnlijker:

(2A) een situatie met vier blauwe ballen links en vier rode ballen rechts, of
(2B) een situatie met twee rode en twee blauwe ballen aan elke kant?

Het verschil tussen deze vraag en de vorige, is dat de vraag nu minder informatie bevat. Uitkomst (2A) beschrijft nog altijd de precieze situatie in afbeelding 1, maar uitkomst (2B) beschrijft naast de situatie in afbeelding 2 bijvoorbeeld ook de situatie in afbeelding 3. Er zijn natuurlijk nog veel meer situaties te bedenken die aan omschrijving (2B) voldoen: met wat uitproberen zien we al snel dat er zes verschillende patronen zijn waarin we twee rode en twee blauwe ballen over de linkerhelft kunnen verdelen. Er zijn voor elk van die zes patronen ook nog eens zes verschillende patronen voor de ballen in de rechterhelft, dus in totaal beschrijven we met omschrijving (2B) maar liefst 6 x 6 = 36 verschillende configuraties.

Elk van die 36 afzonderlijke configuraties is precies even waarschijnlijk als de configuratie uit afbeelding 1. In totaal betekent dat dus, dat het maar liefst 36 maal zo waarschijnlijk is om twee ballen van elke kleur aan elke kant aan te treffen dan het is om alle blauwe ballen links en alle rode ballen rechts te krijgen.

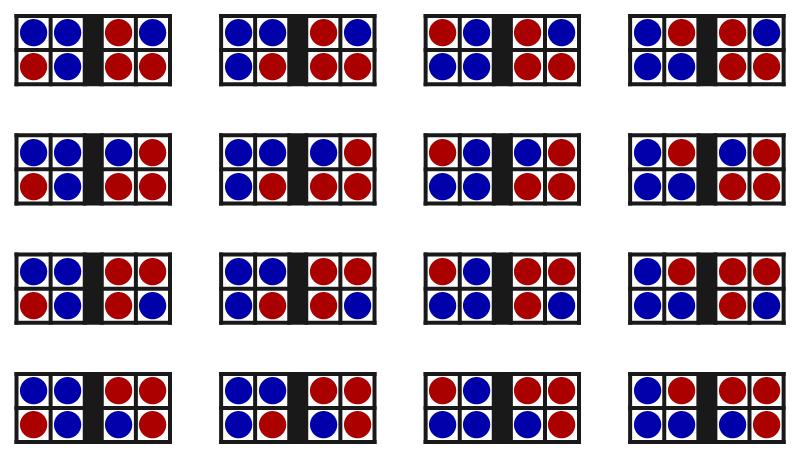
Afbeelding 4. ConfiguratiesDe zestien configuraties voor de situatie “drie blauwe ballen links en één rechts”.

Een soortgelijk sommetje leert ons dat een situatie met drie blauwe ballen links zestien maal zo waarschijnlijk is als de situatie met alle blauwe ballen links – zie afbeelding 4 voor de zestien verschillende configuraties. Ook deze situatie is dus veel waarschijnlijker dan de gesorteerde, maar minder dan half zo waarschijnlijk als de situaties met twee rode ballen aan elke kant. De kans op een situatie met drie blauwe ballen rechts is natuurlijk hetzelfde als die voor drie blauwe ballen links, en de kans op vier blauwe ballen rechts is hetzelfde als de kans op vier blauwe ballen links. Al deze uitkomsten kunnen we weergeven in een grafiek: zie afbeelding 5.

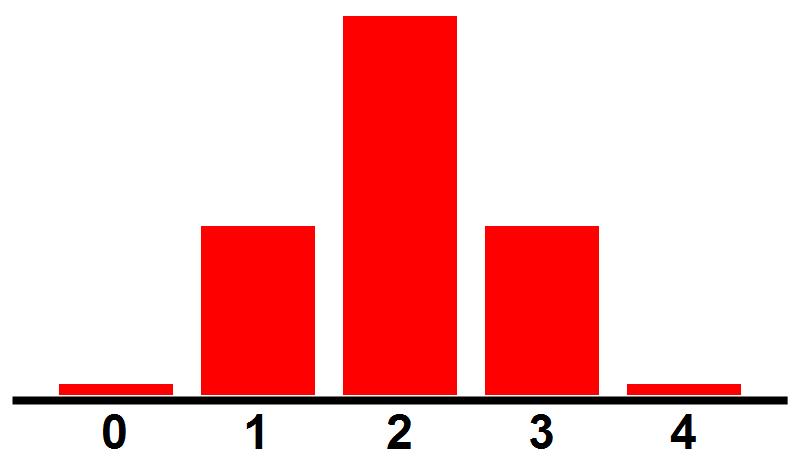
Afbeelding 5. VerdelingenDe waarschijnlijkheid van de verschillende verdelingen in de ballenbak. De getallen geven aan hoeveel blauwe ballen we links aantreffen; de hoogte van de kolommen geeft de waarschijnlijkheid weer.

Waarschijnlijkheid op grote schaal

Uit het voorgaande voorbeeld leren we een belangrijke les. Wanneer we de rode en blauwe ballen willekeurig over de bak verdelen, is de kans op een gelijkmatige verdeling beduidend groter is dan die op een ongelijkmatige. In dit specifieke geval was de meest gelijkmatige verdeling 36 maal zo waarschijnlijk als de meest ongelijkmatige. Dat is al een fors verschil, maar in de wereld van de entropie is het getal 36 nog minuscuul.

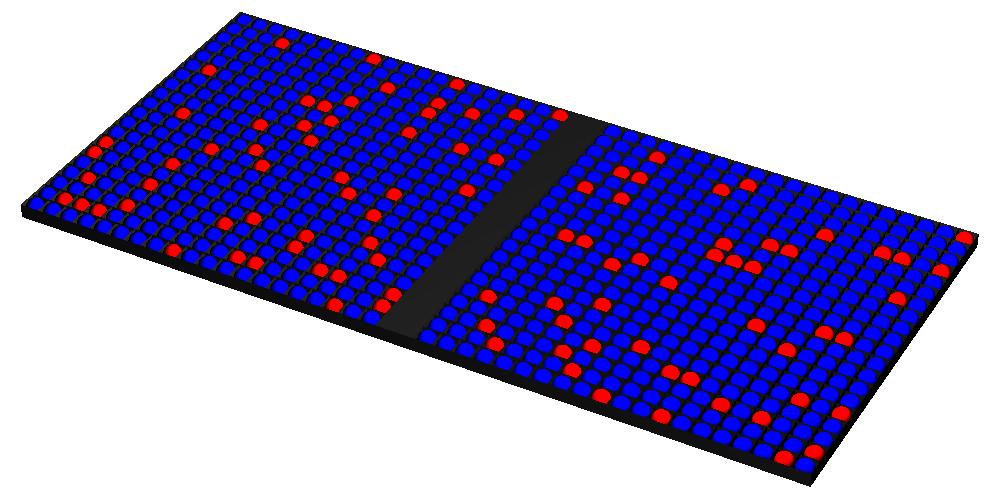
Afbeelding 6. Een ballenbak op grotere schaal

Om een indruk te krijgen van hoe gigantisch groot de getallen kunnen worden, bekijken we nu een soortgelijk voorbeeld op grotere schaal. Ditmaal nemen we een bak waarin beide helften 20 bij 20 vakjes groot zijn. In totaal kan deze bak dus 2 x 20 x 20 = 800 ballen bevatten. In het vorige voorbeeld hadden we evenveel rode als blauwe ballen, maar nu nemen we 100 rode ballen en 700 blauwe. We verdelen deze ballen weer volkomen willekeurig over de vakjes – zie afbeelding 6 voor een voorbeeld.

Zelfs in de meest ongelijkmatige situatie – alle rode ballen aan één kant van de bak – hebben we nu al een gigantisch aantal mogelijkheden. We kunnen immers de 100 rode ballen op heel veel manieren over de 400 vakjes in een van de helften verdelen. Met de hand is nauwelijks meer uit te rekenen hoe groot dat aantal mogelijkheden is, maar een computerprogramma (zoals het rekenprogramma Mathematica) berekent de uitkomst zonder veel problemen. Er blijkt dat we de rode ballen op

2241854791554337561923210387201698554845411177476295990399942258896013-
007429693894018935107174320

verschillende manieren over één van de helften kunnen verdelen. Een getal van maar liefst 97 cijfers – een getal dat groter is dan het aantal elementaire deeltjes in het zichtbare heelal! En dit is nog maar het aantal manieren voor de minst waarschijnlijke verdeling.

De veel waarschijnlijkere verdeling waarbij 50 ballen in de linkerhelft en 50 ballen in de rechterhelft terechtkomen, kan gerealiseerd worden op

29022189803427897872021248811516278126128592168158587590763644022307948-
1193218327138795984664929829737740145115100023594381414400

manieren – een getal van 129 cijfers. Hoewel 129 cijfers niet zo héél veel meer lijkt dan 97, is dit getal toch onnoemelijk veel groter dan het vorige: het is grofweg

129456153506293963269263601811607

maal zo groot. Dat laatste getal lijkt met maar 33 cijfers een “klein” getal vergeleken met de vorige twee monstergetallen, maar het is nog altijd een getal dat vergelijkbaar is met het aantal atomen in de Titanic.

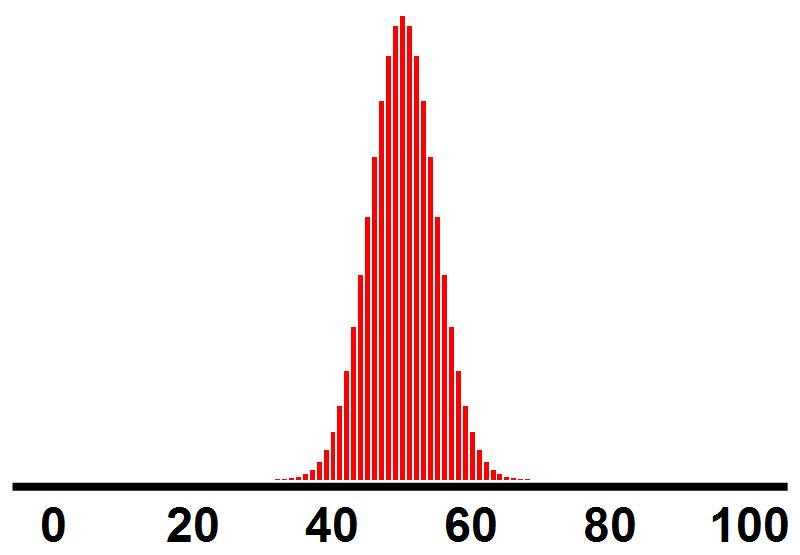
Afbeelding 7. VerdelingenDe waarschijnlijkheid van de verschillende verdelingen in de grotere ballenbak.

De kans dat een willekeurige verdeling gelijkmatig is, is dus ongelooflijk veel groter dan de kans op een extreem ongelijkmatige verdeling. In afbeelding 7 tekenen we een grafiek die aangeeft hoeveel mogelijkheden er per verdeling zijn. De hoogte van de grootste balk komt overeen met het enorme getal van 129 cijfers hierboven. Vanaf verdelingen rond de 30:70 zijn de getallen relatief zó klein dat de rode balken niet meer zichtbaar zijn.

Een toevallige verdeling hoeft dus beslist niet precies 50:50 te zijn. De verdeling zal daar echter zelden veel van afwijken. We zien dit terug in het voorbeeld in afbeelding 6. De computer heeft hier de ballen volkomen willekeurig over de vakjes verdeeld. Het resultaat is dat de linkerhelft 52 rode ballen bevat en de rechterhelft 48 ballen. Laten we de computer de ballen opnieuw verdelen, dan vinden we misschien een verdeling van 49:51, of van 57:43. We zullen echter enorm lang moeten blijven proberen voor we een verdeling met de verhouding 35:65 vinden, en als we willen wachten tot de computer toevallig een verdeling 100:0 produceert, is de totale leeftijd van het heelal in de verste verte nog niet genoeg.

Tot slot in afbeelding 8 een grafiek voor het geval van een bak met 20.000 ballen, waarvan 8.000 rode. We zien dat de verdeling van waarschijnlijkheden hier nog veel meer gepiekt is rond de gemiddelde waarde, 4.000. Hoe groter het aantal ballen, hoe scherper deze piek wordt, en hoe groter dus de waarschijnlijkheid dat we een configuratie zullen vinden die vrijwel precies gelijkmatig verdeeld is.

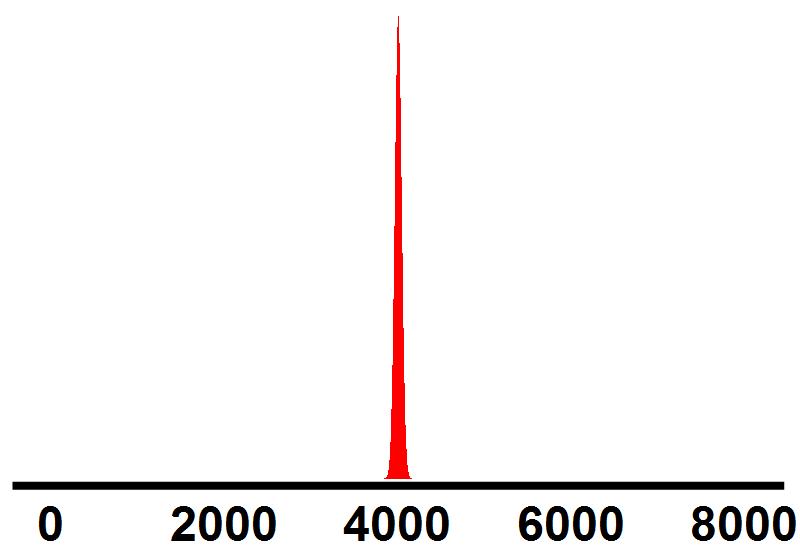
Afbeelding 8. VerdelingenDe waarschijnlijkheid van de verdelingen in een ballenbak met 8.000 rode en 12.000 blauwe ballen.

Dit is het tweede artikel uit het dossier Entropie. In het derde artikel zullen we zien wat microscopische en macroscopische toestanden zijn, en hoe de relatie tussen deze twee de entropie bepaalt.