Entropie (4): Definitie en Tweede Hoofdwet

Definitie 1 (nog niet helemaal precies): de entropie van een macroscopische toestand is het aantal microscopische toestanden dat die macroscopische toestand beschrijft.

Volgens deze (nog wat slordige) definitie is de entropie van de ballenbaktoestand “3:1” dus gelijk aan 16, en van de ballenbaktoestand “2:2” gelijk aan 36. In het geval van een ballenbak met 700 blauwe en 100 ballen, is de entropie van de toestand “50:50” zoals we zagen dan gelijk aan

29022189803427897872021248811516278126128592168158587590763644022307-
9481193218327138795984664929829737740145115100023594381414400.

Dit laatste voorbeeld toont meteen aan wat het grootste probleem is met deze definitie van entropie: de entropie van een realistisch systeem wordt al snel een belachelijk groot getal. Gelukkig bestaat er een wiskundige bewerking die van dergelijke belachelijk grote getallen meer hanteerbare getallen maakt: de logaritme. In het dit artikel wordt uitgelegd hoe de logaritme van een getal precies berekend kan worden. Voor ons zijn met name de volgende eigenschappen van belang:

• De logaritme van een getal x wordt geschreven als log(x).
• Voor grote getallen is de logaritme grofweg gelijk aan 2,3 maal het aantal cijfers dat het getal bevat.
• De logaritme van het getal 1 is gelijk aan 0.

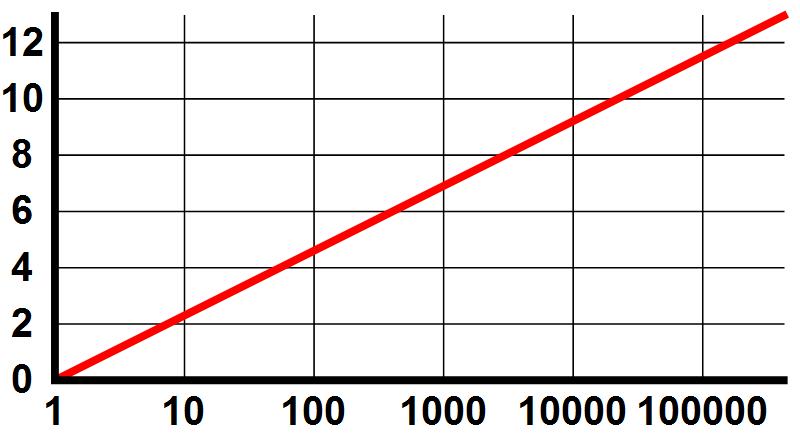
Afbeelding 1. LogaritmesEen grafiek van de logaritmes van een aantal machten van tien. Ook van grote getallen is de logaritme nog een betrekkelijk klein getal.

In de bovenstaande voorbeelden vinden we met behulp van een rekenmachine de volgende logaritmes:

log(16) ≈ 2,77
log(36) ≈ 3,58
log(2902…(nog 121 cijfers)…4400) ≈ 295,80.

Hierin betekent het symbool ≈ dat we de antwoorden, die oneindig veel cijfers achter de komma hebben, hebben afgerond op twee decimalen. We zien dat zelfs van het getal met 129 cijfers de logaritme nog een heel beschaafd getal is. Een veel hanteerbaardere definitie van entropie is dus

Definitie 2 (een heel stuk preciezer): de entropie van een macroscopische toestand is de logaritme van het aantal microscopische toestanden dat die macroscopische toestand beschrijft.

Voor we nog een derde definitie van entropie geven, zullen we eerst een van de belangrijkste toepassingen van het begrip entropie bespreken: de Tweede Hoofdwet van de thermodynamica.

De Tweede Hoofdwet van de thermodynamica

In al onze voorbeelden tot nu toe hebben we gezien dat de “gelijkmatigheid” in de loop van de tijd toeneemt. Gasdruk verdeelt zich gelijkmatig over de gasfles en de omgeving; de temperatuur van een kop thee en de omgeving worden gelijk; de ballen in de ballenbak worden grofweg gelijk over de twee helften verdeeld. De reden daarvoor hebben we inmiddels ook begrepen: die gelijkmatige verdelingen beschrijven een veel groter aantal microscopische toestanden, en zijn daarmee veel waarschijnlijker.

In termen van entropie kunnen we dit als volgt formuleren: de macroscopische toestand waarin het systeem uiteindelijk belandt, is de toestand met de hoogste waarschijnlijkheid – dus met het grootste aantal microscopische toestanden – dus de toestand met de hoogst mogelijke entropie. Dit principe is in de natuurkunde zo belangrijk dat het een aparte naam heeft gekregen: de Tweede Hoofdwet van de thermodynamica.

Tweede Hoofdwet van de thermodynamica: een systeem is in evenwicht als het zijn maximale entropie heeft bereikt. Als een geïsoleerd systeem niet in evenwicht is, zal de entropie toenemen tot het systeem wel in evenwicht is.

Afbeelding 2. Rudolf ClausiusDe Duitse wis- en natuurkundige Rudolf Clausius (1822-1888) gaf in 1856 als eerste een beschrijving van de Tweede Hoofdwet van de thermodynamica in de wiskundige termen die we vandaag de dag gebruiken.

De naam “Tweede Hoofdwet” doet natuurlijk vermoeden dat er nog meer hoofdwetten zijn, en dat is inderdaad het geval. De Eerste Hoofdwet van de thermodynamica kwamen we al eerder tegen: deze wet zegt dat energie altijd behouden blijft. Er is ook nog een Derde Hoofdwet, die zegt dat het begrip “temperatuur” een absoluut nulpunt kent – zo’n 273 graden Celsius onder nul – waarbij elk systeem volledig “bevriest”. Meer over wat “bevriezen” betekent in termen van entropie, zien we verderop in dit artikel.

Soms wordt ook nog een “Nulde Hoofdwet” geformuleerd, die zegt dat als systeem A in evenwicht is met systeem B, en systeem B in evenwicht met systeem C, systeem C ook in evenwicht is met systeem A. Bijvoorbeeld: als de thee in een theekop in thermisch evenwicht is gekomen met de lucht eromheen (en er dus geen warmte meer mee uitwisselt), en als het lepeltje dat in de thee staat ook in thermisch evenwicht is gekomen met de thee (en daar dus ook geen warmte meer mee uitwisselt), dan zal het lepeltje ook met de lucht in thermisch evenwicht zijn, en zullen dus ook het lepeltje en de lucht geen warmte meer uitwisselen.

Het is belangrijk om te beseffen dat de Tweede Hoofdwet gaat over geïsoleerde systemen. Dat wil zeggen: de wet gaat over systemen waarop van buitenaf geen invloed wordt uitgeoefend. Zolang we de thee en de kamer daaromheen met rust laten, zal de thee afkoelen totdat de thee en de lucht in de kamer dezelfde temperatuur hebben bereikt. Dat wil natuurlijk niet zeggen dat we de thee nooit meer kunnen opwarmen: een minuutje op een gasbrander is daarvoor voldoende. De entropie van het niet-geïsoleerde systeem “thee+lucht” neemt dan dus af. Aan de andere kant kunnen we ook het systeem “thee+lucht+gas” beschouwen; dat systeem is wel een geïsoleerd systeem. In dit systeem vinden twee processen plaats: de thee warmt op, maar er ontsnapt ook gas uit het reservoir van de gasbrander. De entropie van “thee+lucht” neemt dus af, maar tegelijkertijd neemt de entropie van het gas toe. Uit de Tweede Hoofdwet volgt dan dat de toename van de entropie van het gas groter moet zijn dan de afname van entropie door de opwarming, zodat de totale entropie van het geïsoleerde systeem “thee+lucht+gas” nog steeds toeneemt.

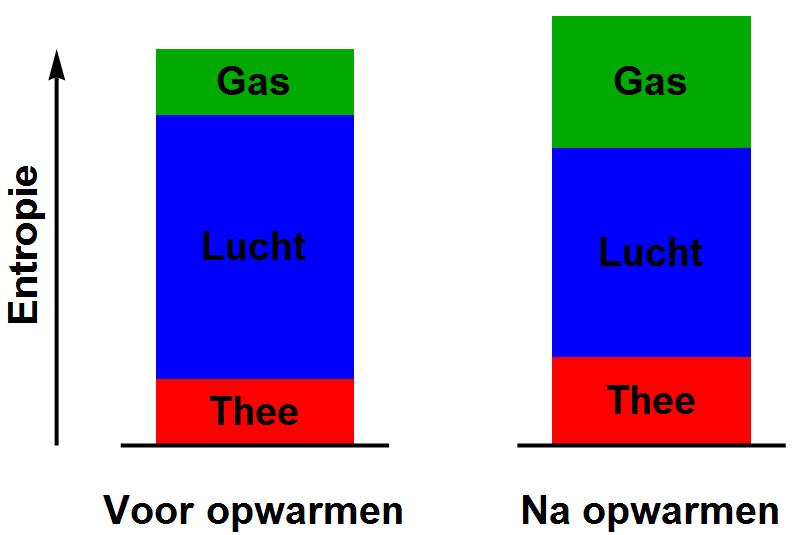
Afbeelding 3. Geïsoleerde systemenDe Tweede Hoofdwet geldt alleen voor geïsoleerde systemen. Wanneer we thee opwarmen zal de lucht in de kamer gemiddeld iets afkoelen; de warmte die de thee opwarmt wordt immers aan de lucht onttrokken. De entropie van de thee neemt daardoor toe, en die van de lucht af. We halen het systeem uit zijn evenwichtstoestand, dus de totale entropie van “thee+lucht” zal ook afnemen. Thee en lucht samen zijn echter geen geïsoleerd systeem: pas als we de entropie van het gas ook meetellen zien we dat de totale entropie van het systeem toeneemt.

Precieze definitie van entropie

We kunnen, zoals we in het vorige hoofdstuk zagen, wel degelijk de entropie van een niet-geïsoleerd systeem laten afnemen, zolang de toename van entropie buiten dat systeem maar voor die afname compenseert. Een voorbeeld van dit verschijnsel is een vriezer. Als we een kom met water in de vriezer zetten, zullen de watermoleculen in de kom steeds langzamer gaan bewegen, tot ze helemaal tot stilstand komen en ijs vormen. IJs heeft een kristalstructuur, waarin alle watermoleculen in een keurig patroon gerangschikt zijn. Zo’n kristal heeft een heel lage entropie vergeleken met die van een kom vloeibaar water: in  vloeibaar water kunnen atomen zich op allerlei plaatsen bevinden en met allerlei snelheden bewegen; in het ijskristal is de plaats van de atomen vastgelegd, en is de snelheid nul. Als we het ijs zover afkoelen dat de atomen in het kristal ook niet meer de energie hebben om te trillen – dat gebeurt bij het eerder genoemde absolute nulpunt van -273⁰C  – heeft het ijsblok dus maar één microscopische toestand, en is de entropie gelijk aan log(1) = 0.

Deze sterke entropieafname die ontstaat als water bevriest, moet natuurlijk elders gecompenseerd worden. De vriezer zal de warmte die aan het ijs wordt onttrokken, afstaan aan de omgeving. Daardoor zal de entropie van de omgeving toenemen.

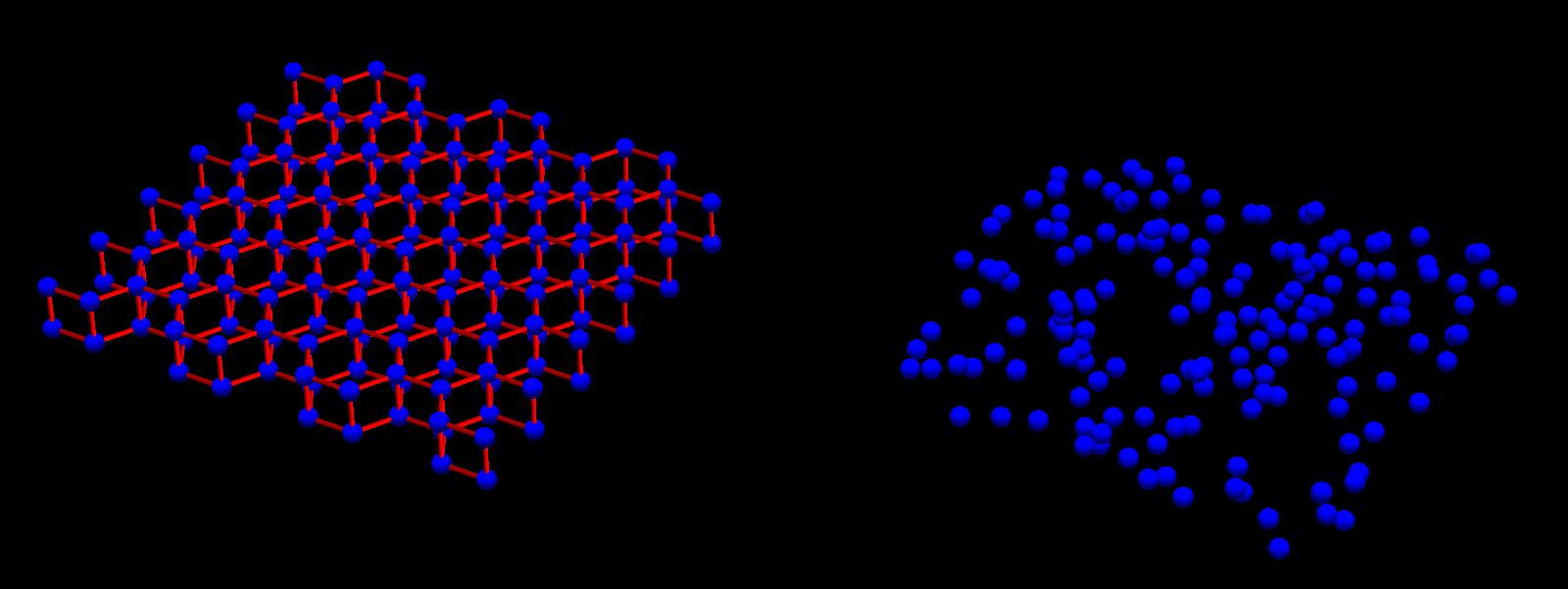
Afbeelding 4. Water en ijsLinks: watermoleculen in een ijskristal. Elk blauw bolletje is een watermolecuul; de rode lijnen zijn toegevoegd om de structuur van het kristal duidelijker weer te geven. Rechts: willekeurig verdeelde watermoleculen in vloeibaar water.

De betekenis van “bevriezen” in termen van entropie is nu duidelijk: als een systeem bevriest en de temperatuur tot het absolute nulpunt daalt, zal de entropie de kleinst mogelijke waarde aannemen. Dit leidt tot een preciezere omschrijving van de Derde Hoofdwet:

Derde Hoofdwet van de thermodynamica: bij het absolute nulpunt van temperatuur (ongeveer -273⁰C) zal elk natuurkundig systeem met bepaalde macroscopische eigenschappen het laagst mogelijke aantal microscopische toestanden hebben, en dus de laagst mogelijke entropie aannemen.

Dat laagst mogelijke aantal microscopische toestanden hoeft natuurlijk niet altijd één te zijn, zoals in het voorbeeld van het bevroren water. Stel bijvoorbeeld dat een mengsel van twee soorten stoffen (A en B) bevriest, en dat die twee stoffen samen een kristal vormen, met op elke plaats in het kristal een atoom van soort A óf van soort B. Het aantal microscopische toestanden van dit systeem zal beduidend hoger zijn dan 1. Zelfs een kristal van maar vier atomen, twee van elke soort, heeft als mogelijke toestanden

AABB, ABAB, ABBA, BAAB, BABA en BBAA,

dus in totaal zes verschillende toestanden. Bij grotere kristallen neemt het aantal mogelijkheden weer exponentieel toe. Zo’n “gemengd kristal” zal ook bij het absolute nulpunt dus veel meer dan één mogelijke toestand hebben. Dat neemt niet weg dat het aantal mogelijke toestanden wél minimaal is: bij hogere temperaturen zal er een nog veel groter aantal mogelijkheden zijn, omdat de atomen nu ook kunnen trillen, en dus allerlei verschillende trillingstoestanden kunnen hebben.

Afbeelding 5. Een eenvoudig kristalDe zes mogelijke toestanden van een “mini-kristal” dat bestaat uit twee atomen van soort A en twee van soort B.

Dit leidt ons tot onze uiteindelijke definitie van entropie. We nemen het minimale aantal toestanden van een systeem als een “ijkpunt”, en definiëren

Definitie 3 (helemaal precies): de entropie van een macroscopische toestand is de logaritme van het aantal microscopische toestanden dat die macroscopische toestand beschrijft, gedeeld door het aantal microscopische toestanden bij het absolute nulpunt van temperatuur.

Stel dat ons mini-kristal van hierboven bij een bepaalde lage temperatuur bijvoorbeeld precies genoeg energie heeft om één atoom te laten trillen. In dat geval heeft het systeem 24 mogelijke toestanden: het kristal AABB waarbij het linkeratoom trilt, het kristal AABB waarbij het tweede atoom trilt, enzovoort. Bij het absolute nulpunt heeft het systeem geen trillingsmogelijkheden meer, en dus alleen de zes microscopische toestanden die we hierboven noemden. De entropie van de iets opgewarmde toestand is dus

log(24/6) = log(4) ≈ 1,39.

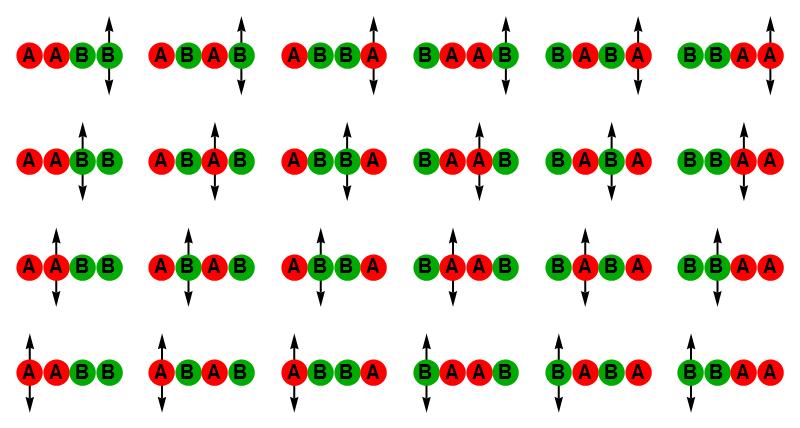
Afbeelding 6. Een trillend kristalDe 24 mogelijke toestanden waarin het kristal een klein beetje is opgewarmd, zodat één van de atomen begint te trillen.

Bij het absolute nulpunt zelf kunnen we natuurlijk ook de entropie uitrekenen: in dat geval levert het feit dat we geen trillingstoestanden meer hebben het nogal triviale resultaat

log(6/6) = log(1) = 0.

De logaritme van het getal 1 is gelijk aan 0, en dus is de entropie van elk systeem bij het absolute nulpunt in onze nieuwe definitie precies gelijk aan nul. Dit is de belangrijkste reden voor het kiezen van de bovenstaande definitie.

Entropie en faseruimte

Laten we onze volledige definitie van het begrip entropie nog eens herhalen:

De entropie van een macroscopische toestand is de logaritme van het aantal microscopische toestanden dat die macroscopische toestand beschrijft, gedeeld door het aantal microscopische toestanden bij het absolute nulpunt van temperatuur.

Deze definitie werkt heel goed voor eenvoudige systemen zoals onze ballenbak, maar leidt voor ingewikkelder systemen vaak tot de volgende verwarring. Wat gebeurt er als het aantal microscopische toestanden van een systeem oneindig groot is?

Dat dit een probleem is, is al duidelijk als we een heel eenvoudig systeem bekijken: een gasfles met daarin een gas dat bestaat uit maar één atoom. Dat atoom kan zich precies midden in de gasfles bevinden, of een centimeter links van het midden, of 0,37 centimeter daarboven, of 0,32764536 centimeter naar achteren… Het moge duidelijk zijn dat er een oneindig aantal mogelijke posities voor het atoom is. Hoe kunnen we uit dit oneindige aantal toestanden een zinvolle entropie berekenen?

Het antwoord is dat we zo’n oneindig aantal toestanden niet kunnen tellen, maar vaak wel kunnen meten. Bijvoorbeeld: als onze gasfles een volume van 2 liter heeft, kunnen we zeggen dat de positie van het ene atoom in de gasfles “2 liter aan mogelijke toestanden” heeft. Als de kamer waarin de gasfles staat een volume van 10.000 liter heeft, heeft de positie van een atoom buiten de gasfles 10.000 liter aan mogelijke toestanden. Het “aantal” toestanden van het atoom buiten de gasfles is dus 5000 maal zo groot als het “aantal” toestanden binnen de gasfles.

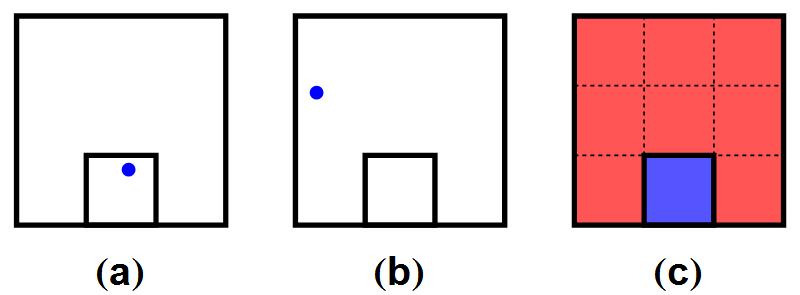
Afbeelding 7. Het “tellen” van oneindig veel toestandenEen gasfles (het kleine vierkant) in een kamer (het grote vierkant). Een atoom in de gasfles (a) kan zich op oneindig veel mogelijke posities bevinden. Hetzelfde geldt voor een atoom buiten de gasfles (b). We kunnen de toestanden niet tellen, maar wel meten. Zo is uit figuur (c) bijvoorbeeld duidelijk dat het “aantal” toestanden buiten de gasfles (rood) hier acht maal zo groot is als het “aantal” toestanden binnen de gasfles (blauw).

Hoewel we de individuele microscopische toestanden niet meer kunnen tellen, is de verhouding van twee “aantallen” toestanden nog steeds goed gedefinieerd. En aangezien de bovenstaande definitie van entropie gebaseerd is op zo’n verhouding, kunnen we ook in dit geval de entropie van een bepaalde macroscopische toestand uitrekenen.

Hetzelfde geldt als we meer dan één atoom hebben. Laten we bijvoorbeeld eens kijken naar een systeem met twee atomen, en laten we voor het rekengemak de “kamer” even groot maken als de gasfles: beide hebben nu een volume van 2 liter. Wat is dan het “aantal” toestanden dat overeenkomt met de verdeling “2:0”, dus met “twee atomen in de gasfles, en geen atomen in de kamer”? Het eerste atoom heeft 2 liter aan mogelijke toestanden in de kamer, het tweede ook, dus het totale “aantal” toestanden kunnen we berekenen als

(2 liter) x (2 liter) = 4 liter²

De eenheid “liter²” komt hier misschien wat vreemd over, maar is in dit voorbeeld de correcte natuurkundige maat om het “aantal” mee te meten. Vergelijk het met het meten van een oppervlak: een vierkant met een lengte van 2m en een breedte van 2m heeft een oppervlakte van 4m².

De toestand “0:2” heeft natuurlijk hetzelfde “aantal” toestanden. Hoe zit het met de toestand “1:1”? Die toestand kunnen we op twee manieren bereiken: met atoom 1 in de gasfles en atoom 2 erbuiten, of met atoom 2 in de gasfles en atoom 1 erbuiten. Elk individueel atoom heeft in elk van die gevallen 2 liter aan mogelijke toestanden, dus het totale “aantal” wordt dan

(2 liter) x (2 liter) + (2 liter) x (2 liter) = 8 liter²

We zien dat deze uitkomst tweemaal zo groot is als de vorige, en dat daarmee de toestand “1:1” dus tweemaal zo waarschijnlijk is als de toestand “2:0”. Ook hier geldt dus weer dat de gelijkmatige macroscopische toestand de meest waarschijnlijke is.

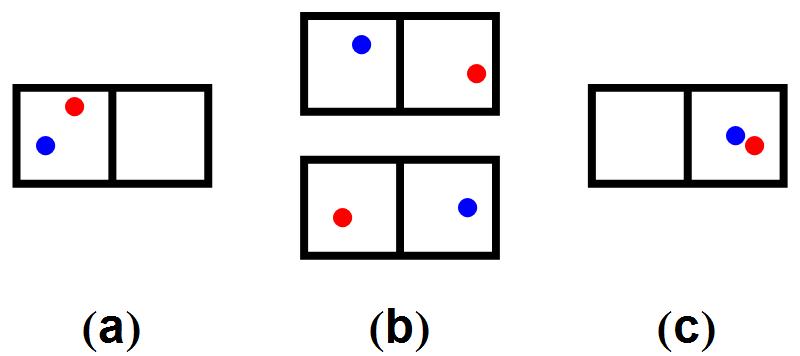
Afbeelding 8. De maat van verschillende macroscopische toestandenDe macroscopische toestand “2:0” (a) komt overeen met 2 liter x 2 liter = 4 liter² aan mogelijke microscopische toestanden. Hetzelfde geldt voor de toestand “0:2” in afbeelding (c). Het “aantal” microscopische toestanden voor de toestand “1:1” (b) is tweemaal zo groot.

Dit voorbeeld kan nog verder worden uitgebreid, natuurlijk naar meer atomen, maar ook naar situaties waarin we bijvoorbeeld ook de verschillende mogelijke snelheden van de atomen meetellen in het aantal mogelijke toestanden.

De moraal van het verhaal is dat het aantal mogelijke toestanden in al deze gevallen gemeten kan worden als een “volume”. Dit volume is in het algemeen een hogerdimensionaal volume – we zagen hierboven bijvoorbeeld al een volume in liter². De abstracte ruimte waarin we dit volume meten wordt de faseruimte genoemd. Deze website bevat een apart dossier over het begrip “faseruimte” waarin de details van deze constructie verder worden uitgelegd.

Een opmerking tot slot: vrijwel elk systeem dat we kunnen bedenken, lijkt op het eerste gezicht een oneindig aantal toestanden te hebben. Posities, snelheden, enzovoort, kunnen immers altijd een oneindig aantal waarden aannemen. Dit is in de “klassieke” natuurkunde inderdaad het geval. In een quantummechanische beschrijving van de natuur is het echter vaak zo dat al dit soort eigenschappen toch maar een eindig aantal waarden kan aannemen – dat is precies waar de term “quantisatie” op duidt. Bijvoorbeeld: de snelheid van een elektron dat rond een atoomkern draait, kan alleen een serie heel precies bepaalde waarden aannemen, maar geen snelheden die tussen die waarden in liggen. Ook dit wordt in het artikel over faseruimtes verder uitgelegd. In de quantummechanica komen we dus vaak weer terug bij de oorspronkelijke definitie van entropie, waarin we de microscopische toestanden van een systeem letterlijk kunnen tellen.

Dit is het vierde artikel uit het dossier Entropie. In het vijfde artikel bespreken we de rol die entropie speelt in de thermodynamica.