Bekijk eens het volgende korte filmpje:
Dit filmpje laat een voorbeeld zien van het tennisracketeffect, dat ook wel het Dzhanibekov-effect wordt genoemd, naar de Sovjet-astronaut die het opmerkte tijdens een ruimtereis in 1985. Dat het verschijnsel zich ook in het filmpje in de ruimte afspeelt, zorgt ervoor dat we het goed kunnen bekijken omdat de hendel niet naar beneden valt, maar gewichtloosheid is voor het effect niet noodzakelijk. Op aarde is precies hetzelfde aan de hand.
Wat gebeurt hier precies? Veel objecten, zoals een tennisracket, maar ook bijvoorbeeld een boek of je mobiele telefoon, hebben een aantal symmetrie-vlakken, en daardoor drie mogelijke “natuurlijke” assen om rond te draaien. Deze assen zijn voor het voorbeeld van een tennisracket getekend in afbeelding 1.
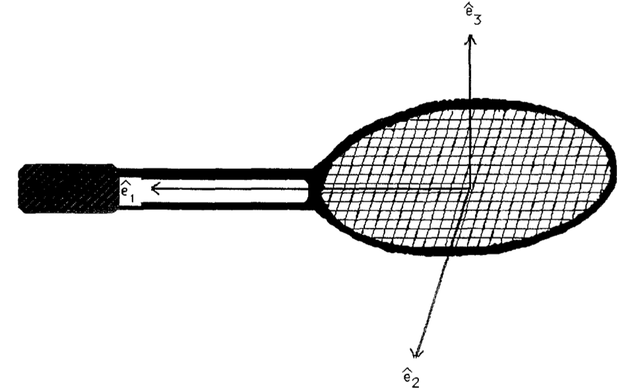
Afbeelding 1. De drie draaiassen van een tennisracket.De drie natuurlijke draai-assen (hoofdassen, principal axis in het Engels) van een tennisracket. Afbeelding uit The Twisting Tennis Racket, Mark S. Ashbaugh, Carmen C. Chicone and Richard H. Cushman (1991), Journal of Dynamics and Differential Equations.
De opvallende waarneming die Dzhanibekov deed, en die natuurkundigen Mark Ashbaugh, Carmen Chicone en Richard Cushman vervolgens in 1989 in een publicatie in detail uitwerkten, was de volgende. Als je het racket om de eerste of derde as in het plaatje hierboven draait, is de draaiing stabiel. Er gebeurt dan precies wat je zou verwachten en het voorwerp blijft rustig draaien om de as. Draai je het racket echter om de tweede as, aangegeven met e2, dan is de draaiing niet stabiel! Dit is wat er in het filmpje ook met de hendel gebeurt.
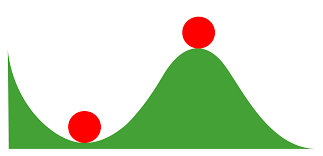
Afbeelding 2. Stabiel en instabiel.Het linker balletje is in een stabiele evenwichtstoestand; het rechter balletje in een instabiele.
Dat iets stabiel is, betekent in natuurkundige termen dat, als je een beetje afwijkt van de situatie, die vanzelf weer terugkeert naar de begintoestand. Een voorbeeld is de linker bal in afbeelding 2. Als deze bal een beetje schommelt, komt hij altijd weer in het midden van het dal terecht. Ditzelfde is het geval met de draaiingen rondom de eerste en derde as van ons tennisracket. Als het enigszins waait, of als je de draaiing begint met een kleine afwijking, zal het racket zichzelf corrigeren en toch weer precies rond de as gaan draaien.
Een instabiele situatie is te vergelijken met het rechter balletje. Deze bal is nu nog in evenwicht, maar het kleinste zuchtje wind kan er voor zorgen dat hij uit evenwicht raakt, naar beneden rolt en vervolgens nooit meer terugkomt op de berg. Dit is vergelijkbaar met de situatie als je het tennisracket om de tweede as e2 draait. Als gevolg van deze instabiliteit draait ook de hendel in het filmpje steeds om. Natuurlijk zou je met héél nauwkeurig draaien in principe het racket ook stabiel om deze as kunnen laten draaien, net zoals je héél voorzichtig het balletje op de heuvel kunt laten balanceren, maar helaas is het zo dat wij als mensen nooit iets zo precies zouden kunnen laten draaien dat het niet eens een beetje afwijkt van de as. Daarnaast is er altijd wind en zijn er allerlei andere vormen van storing. Daarom zal een draaiing rondom de tweede as altijd zorgen voor dit verbazingwekkende resultaat.

Afbeelding 3. Een tennisracket.Probeer het zelf: rond welke as kun je een tennisracket wel en niet gemakkelijk laten draaien? Foto: Riadh Dallel.
De reden dat juist de tweede as een instabiele draaiing heeft, is dat deze as ook het middelste traagheidsmoment heeft. Het traagheidsmoment van een voorwerp met betrekking tot een bepaalde draai-as is een grootheid die uitdrukt hoe makkelijk of moeilijk het is om het voorwerp te laten draaien rondom die as. Je kunt je misschien voorstellen dat draaien rondom as e1 het gemakkelijkst gaat (as e1 heeft het kleinste traagheidsmoment) omdat het tennisracket het smalst is rondom die richting. As e3 is juist het moeilijkst om het racket om rond te draaien – deze as heeft dus het grootste traagheidsmoment – en de tweede as zit daar tussenin.
Het wiskundige bewijs dat juist draaiing rond die middelste as instabiel is, is nog best lastig (zie bijvoorbeeld hier) en onze intuïtie helpt ons hier ook niet heel veel verder. Maar goed, je kan het gelukkig zelf wel gewoon proberen! Pak maar eens een tennisracket, boek, telefoon of ander voorwerp en je zal ondervinden dat het tennisracketeffect echt bestaat.