
Afbeelding 1. Hoe weeg je de aarde?Foto: Pickpik.
De Principia
Het verhaal begint met een van de grootste revoluties uit de geschiedenis van de natuurkunde: de publicatie in 1687 van Sir Isaac Newton’s meesterwerk, de Philosophiae Naturalis Principia Mathematica, beter bekend als de Principia. Centraal in dit werk staat een aantal wetten die beschrijven hoe objecten onder invloed van een kracht bewegen. Een van deze wetten is Newton’s universele zwaartekrachtswet. Die wet zegt grofweg dat alle objecten in het universum een kracht op elkaar uitoefenen. Newton realiseerde zich dat deze kracht evenredig is met de massa (M, m) van ieder object en omgekeerd evenredig met het kwadraat van de afstand (r) tussen de objecten. Dat kan mooi worden samengevat in de volgende formule:
![]()
De F staat hier voor de kracht (‘force’) en G is een bepaalde omrekenconstante, tegenwoordig bekend als de ‘constante van Newton’. De wetten van Newton hebben enorm veel toepassingen binnen de natuurkunde: van de beweging van planeten en de oorsprong van getijden tot de baan van een kanonskogel. Daarom duurde het ook even voordat alle gevolgen duidelijk zichtbaar waren.
In de Principia schreef Newton over het vermoeden dat een slinger, wanneer je hem dichtbij een berg hangt, een heel kleine afwijking in de richting van de berg zou hebben. (Een ‘slinger’ is in principe niet meer dan een gewicht aan een touwtje, dat je kunt gebruiken om te meten in welke richting de zwaartekracht precies trekt. Om dat heel nauwkeurig te doen helpt het overigens om de slinger daadwerkelijk te laten slingeren, en over een lange tijdsperiode de gemiddelde positie te meten.) De afwijking van de slinger is het gevolg van de zwaartekracht die de berg op de slinger uitoefent. De precieze afwijking zou je via de bovenstaande formule kunnen berekenen uit de verhouding tussen het gewicht van de berg en het gewicht van aarde. In tegenstelling tot wat je misschien op het eerste gezicht zou denken, is dit een opmerking met grote gevolgen! Als je namelijk in staat bent om deze afwijking heel precies te meten, én je weet hoe zwaar de berg is, dan zou je dit in theorie kunnen gebruiken om een nauwkeurige schatting te geven van de massa van de aarde. Newton ging er echter vanuit dat de afwijking in de praktijk te klein was om te meten en verwierp het experiment om deze reden. Gelukkig bleek Newtons pessimisme ongegrond.
Hoe vind je een geschikte berg?
Een kleine eeuw later, in 1772, werd het probleem opgepakt door Nevil Maskelyne, de Britse Astronomer Royal (koninklijke astronoom) van dat moment. Hij was ervan overtuigd dat het door Newton beschreven effect wél meetbaar moest zijn en had ook een idee over hoe je zo’n meting zou moeten aanpakken. Via astronomische waarnemingen aan de sterrenhemel zou je de afwijkingshoek tot op goede precisie kunnen meten. In afbeelding 2 zie je hoe dit ongeveer werkt. Het voornaamste probleem was volgens Maskelyne om een berg te vinden waarvan de vorm zo regelmatig en symmetrisch was dat je een goede schatting van zijn massa kon maken. Na enige tijd wist hij de Royal Society ervan te overtuigen om een expeditie op te zetten, onder leiding van een Engelse astronoom genaamd Charles Mason, om een geschikte berg te vinden.
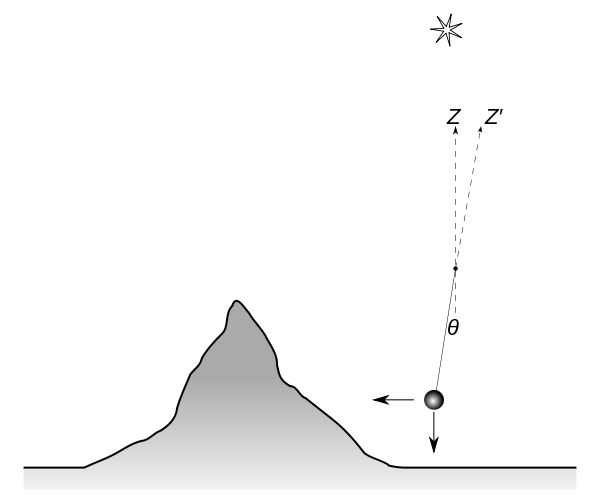
Afbeelding 2. Zwaartekracht naast een berg.Normaal gesproken hangt een slinger recht naar beneden als gevolg van de zwaartekracht van de aarde. Wanneer je de slinger echter in de buurt van een zwaar genoeg object hangt, zoals een berg, dan zorgt de zwaartekracht van de berg voor een kleine afwijking in de richting van de berg. Deze hoek is dan te meten door de sterrenhemel als referentiekader te gebruiken. Afbeelding: BillC.
Maskelyne en Mason hadden elkaar elf jaar eerder leren kennen tijdens een project om een andere astronomische meting te doen van historische proporties: de overgang van Venus over het oppervlak van de zon in 1761, die gebruikt werd om de afstand van de aarde naar de zon nauwkeurig te bepalen. Charles Mason is vandaag de dag voornamelijk bekend door zijn werk aan het in kaart brengen van de `Mason-Dixon line’ in de Verenigde Staten, een grens die tijdens de Amerikaanse burgeroorlog een symbolische status heeft gekregen als de scheidslijn tussen de vrije en de slavenstaten. In 1773 nam Mason het op zich om een geschikte berg te vinden voor het experiment en na een lange zoektocht vond hij een kandidaat in de centrale Schotse Hooglanden, een berg genaamd Schiehallion. Deze berg lag redelijk geïsoleerd van omringende heuvels en was symmetrisch genoeg om een redelijke schatting van z’n volume te kunnen doen. In afbeelding 3 is een aanzicht van Schiehallion te zien. Mason was echter niet van plan om zelf daadwerkelijk de metingen te gaan doen, en trok zich vervolgens terug uit de samenwerking.

Afbeelding 3. De Schiehallion.Links: De berg Schiehallion in Schotland. Foto: Andrew2606. Rechts: Een plakkaat dat nu vlakbij de berg te vinden is. Foto: David Purchase.
Daarmee viel Maskelyne zelf de eer te beurt om het ‘Schiehallion-experiment’ uit te voeren. In de zomer van 1774 woonde hij voor grofweg vier maanden in een tentje op de Schotse Hooglanden en stuurde daar een groep astronomen en landmeters aan om talloze metingen te doen aan deze berg en de sterrenhemel. Zowel de meting van de afwijkingshoek als het in kaart brengen van de berg hadden echter veel voeten in de aarde en werden geplaagd door slechte weersomstandigheden. Daarnaast werden de berekeningen al snel zo ingewikkeld dat Maskelyne de hulp moest inroepen van een wiskundige, Charles Hutton. Nadat de landmeters de hele berg in kaart hadden gebracht was het aan Hutton om uit al deze data een redelijke schatting te maken van het volume, en dus het gewicht, van de berg.
Hutton voelde zich genoodzaakt om wat overzicht te brengen in deze chaos en bedacht dat het handig was om op de kaarten punten van dezelfde hoogte met een lijn te verbinden. Daarmee was Hutton de eerste die hoogtelijnen gebruikte, nu een van de belangrijkste technieken in de cartografie. In 1776 was het werk eindelijk voltooid: met het gewicht van de berg Schiehallion en de astronomische waarnemingen van de afwijkingshoek kon Hutton een schatting geven van de massa van de aarde. Hij vond een waarde van ongeveer 5 quadriljoen kilogram. De aarde had dan eindelijk een vastgesteld gewicht – maar klopte dat gewicht ook?
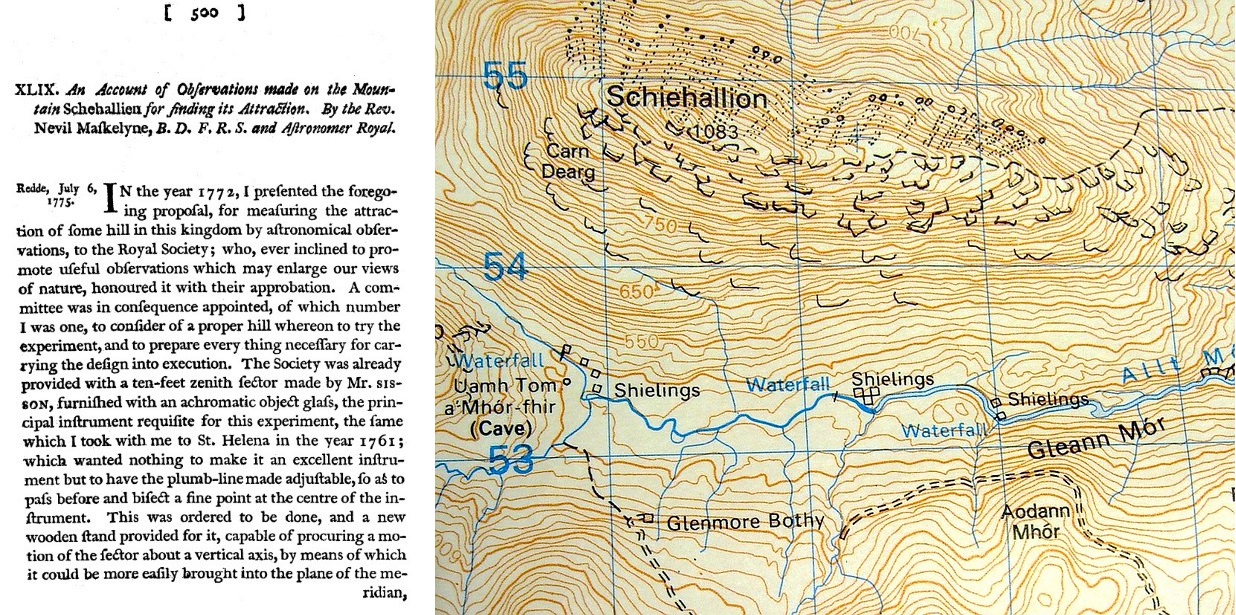
Afbeelding 4. Het meten van een berg.Links: Een pagina uit het logboek van Nevil Maskelyne over hun bevindingen tijdens het Schiehallion experiment. Rechts: Het gebruik van hoogtelijnen. Kaart: Stuart Anthony.
Het Cavendish-experiment
Niet iedereen was tevreden met dit resultaat. Zo had Hutton in zijn berekingen een schatting gemaakt van de dichtheid van de berg, maar dit was niet meer dan een `educated guess’. Eén van deze criticasters was John Michell, een gerenommeerde Britse wetenschapper. Een opmerkelijke feit over Michell is dat hij zo’n tweehonderd jaar voordat Albert Eintein met zijn relativiteitstheorie kwam al het bestaan van zwarte gaten postuleerde. Maar hij heeft waarschijnlijk de grootste impact gehad met de constructie van een machine om de massa van de aarde te bepalen. Voordat Michell echter tijd had om het experiment zelf uit te voeren overleed hij. Zijn constructie kwam terecht bij de natuurkundige Henry Cavendish, aan wie Michell het had nagelaten. Cavendish stond bekend als een briljante, maar ietwat excentrieke persoonlijkheid. Zo gaat het verhaal dat hij leed aan een extreme vorm van pleinvrees en was hij berucht om het niet publiceren van zijn wetenschappelijke resultaten. Zonder iemand erover te vertellen had Cavendish onder andere de wet van behoud van energie, de wet van Ohm en het principe van elektrische geleiding gevonden of geanticipeerd, ver voordat ze daadwerkelijk bekend werden in de natuurkundige gemeenschap. Hij is echter als natuurkundige het meest bekend geworden om een experiment dat hij in 1797 uitvoerde.
Op zevenenzestigjarige leeftijd boog Cavendish zich over de spullen die John Michell hem had nagelaten. De machine die Cavendish uiteindelijk in elkaar zette, bestond uit een ingewikkelde constructie van gewichten, tegengewichten en slingers. In het midden hingen twee grote loden ballen met elk aan één kant een kleinere bal. Een tekening van deze opstelling is in afbeelding 5 weergeven. Het idee van het experiment was om de zwaartekracht van de grote op de kleine ballen te meten. In vergelijking met het Schiehallion-experiment was een voordeel van deze opstelling dat de massa van de grote ballen bekend was; een nadeel natuurlijk dat de te meten afwijking vele malen kleiner was dan in het Schiehallion-experiment.
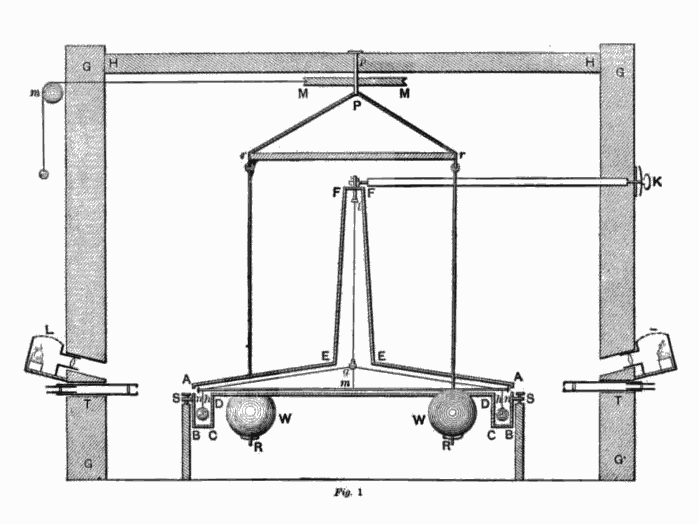
Afbeelding 5. Het experiment.Een tekening uit Cavendish’ eigen beschrijving van het experiment.
Zwaartekracht wordt vaak gezien als een relatief sterke kracht, omdat de kracht planeten in hun baan houdt en dingen met een klap op de grond laat vallen. Dit komt echter alleen door de enorme massa’s die er in deze voorbeelden aanwezig zijn: die van de zon en van de aarde. Op een fundamenteel niveau is zwaartekracht een verbluffend zwakke kracht. Iedere keer dat je iets van de grond opraapt overwin je de zwaartekracht van een gehele planeet! Het experiment dat Cavendish probeerde uit te voeren moest de effecten van zwaartekracht meten op dit heel zwakke niveau. Daarmee was de bepaling van de afwijking een extreem delicate onderneming: de kleinste trilling of het zwakste briesje zou de meting al verpesten. Het uiteindelijke experiment bestond uit zeventien heel precieze metingen die op afstand moesten worden gedaan, en het koste Cavendish ongeveer een jaar om het experiment volledig af te ronden. Maar niet zonder resultaat: de waarde die Cavendish vond, zo’n 20% meer dan wat Hutton had gemeten, zit nog steeds binnen 1% van de huidige schatting die we hebben van het gewicht van de aarde! Een mooie bijkomstigheid van dit resultaat is dat men nu niet alleen wist hoe zwaar de aarde was, maar daarmee ook de gewichten van de zon, de maan en de planeten in ons zonnestelsel kon berekenen. Newton’s formule kon namelijk opnieuw worden gebruikt om de relatieve verhoudingen tussen al deze massa’s te berekenen. En dat allemaal zonder dat Cavendish ook maar zijn huis hoefde te verlaten!
Hoe weeg je de aarde? We hebben gezien hoe wetenschappers soms jaren van hun leven bezig zijn geweest om deze vraag te beantwoorden. Met behulp van theoretische onderbouwing in de vorm van Newtons zwaartekrachtswet en natuurkundige experimenten die op het eerste gezicht onmogelijk uitvoerbaar leken, had men al voor het begin van de negentiende eeuw de aarde gewogen. Misschien dat je hier nog eens aan denkt als je de volgende keer iets op een weegschaal legt.
[1] Het zou preciezer zijn om hier het woord `massa’ te gebruiken. Het gewicht van een object hangt namelijk af van waar je het meet: als ik op een weegschaal ga staan op de maan is mijn gewicht anders dan op aarde, maar mijn massa blijft hetzelfde. Net als in normale spreektaal gebruiken we in dit artikel beide termen door elkaar.