Priemgetallen zijn de bouwstenen van ons getallensysteem. De reeks van deze getallen – die enkel deelbaar zijn door zichzelf en door het getal 1 – begint met 2, 3, 5, 7, 11, 13, 17, 19, 23, … en gaat zo door tot in het oneindige. De vraag die wiskundigen al eeuwen heeft beziggehouden is of er een bepaalde structuur zit in de verdeling van deze priemgetallen. In 1859 heeft de Duitse wiskundige Bernhard Riemann voorgesteld dat de verdeling van priemgetallen niet geheel willekeurig is maar bepaald kan worden aan de hand van andere getallen, de ‘niet-triviale nulpunten van de zètafunctie’. De Riemannhypothese is een vermoeden over waar deze nulpunten zich bevinden, en het vinden van een bewijs (of tegenvoorbeeld) voor dit vermoeden wordt gezien als de heilige graal van de wiskunde. In dit artikel, het derde uit onze reeks over toevalsmatrices (deel 1, deel 2), zullen we zien hoe ideeën uit de natuurkunde – en in het bijzonder over zulke toevalsmatrices – wellicht kunnen leiden tot een bewijs van deze beroemde hypothese.
A million dollar question
Vlak na de eeuwwisseling stelde het Clay Mathematics Institute een lijst op van zeven wiskundige problemen. Deze `millenniumproblemen’, zoals ze nu ook wel bekend staan, werden zó belangrijk gevonden dat er $1.000.000 te verdienen valt door diegene die een oplossing weet te vinden. Een van deze problemen is het bewijzen (of ontkrachten) van de Riemannhypothese. Maar wat zegt die hypothese nu precies? Om dit te kunnen begrijpen hebben we één belangrijk ingrediënt nodig: complexe getallen.
Complexe getallen hebben de vorm a + b i waarbij i een zogenaamd `imaginair’ getal is met de eigenschap dat i2 = -1. Hier doe je dus eigenlijk iets wat je normaal gesproken niet mag doen: je neemt de wortel van een negatief getal, i = √(-1). Dit is ook de reden waarom de term `imaginair’ gebruikt wordt: de reële getallen die je normaal gesproken tegenkomt, bijvoorbeeld -3, 25 of π, worden nooit negatief als je ze kwadrateert. Een complex getal wordt vaak weergeven als een punt in het complexe vlak, zie afbeelding 1 hieronder, waarbij de x-coördinaat gelijk is aan het ‘reële deel’ a en de y-coördinaat aan het ‘imaginaire deel’ b.

Afbeelding 1. Het complexe vlak.Punten in dit vlak geven complexe getallen weer. Afbeelding: Wolfkeeper.
Je kunt complexe getallen gewoon optellen en vermenigvuldigen zoals normale getallen, als je bij het vermenigvuldigen maar onthoudt dat i2 = -1. Bijvoorbeeld: (4 + 5i) ∙ 2i = 8i + 10i2 = -10 + 8i.
De Riemannhypothese zegt iets over de Riemann-zètafunctie, meestal aangeduid met Griekse letter zèta (vandaar de naam) als ζ(s). De zètafunctie neemt als input een complex getal s en geeft als uitkomst een ander complex getal. Voor sommige getallen geeft de zèta-functie nul als uitkomst: ζ(s) = 0. Er zijn triviale nulpunten, waarvan we precies weten waar ze liggen, namelijk s=-2,-4,-6, …, maar deze nulpunten zijn voor ons verhaal niet zo belangrijk. Veel interessanter zijn alle andere nulpunten, waarvan we niet exact weten waar ze liggen. Riemann heeft in zijn artikel “Über die Anzahl der Primzahlen unter einer gegebenen Grösse” een formule beschreven waarmee je het aantal priemgetallen onder een bepaalde grens kunt berekenen door de nulpunten van de zètafunctie bij elkaar op te tellen. Riemanns formule werkt echter alleen wanneer de niet-triviale nulpunten een heel specifieke vorm hebben:
s = ½ + i t.
Het reële deel van de nulpunten moet dus exact gelijk zijn aan ½. In het complexe vlak liggen deze punten op de zogeheten kritieke lijn, zie afbeelding 2 hieronder. Het lukte Riemann om voor de eerste paar nulpunten na te gaan dat ze inderdaad op de kritieke lijn liggen. Dit gaf hem genoeg vertrouwen om het vermoeden uit te spreken dat alle nulpunten op de kritieke lijn liggen. Het lukte hem echter niet om een algemeen bewijs te vinden. Zoals hij zelf al schreef: “Het zou zeker wenselijk zijn om een formeel bewijs te hebben.”
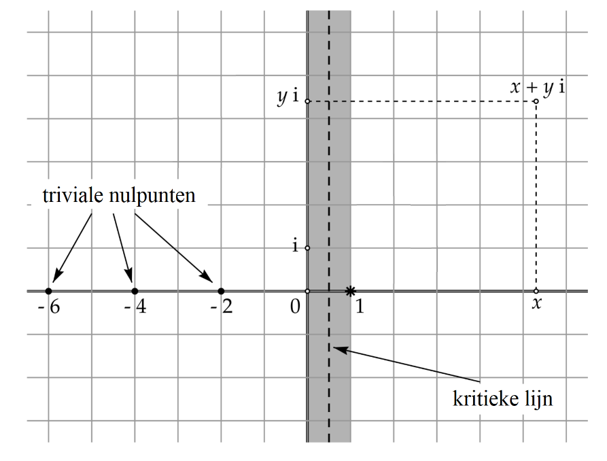
Afbeelding 2. De kritieke lijn in het complexe vlak.De Riemannhypothese zegt dat alle niet-triviale nulpunten van de zètafunctie op deze kritieke lijn liggen. Afbeelding uit Nulpunten op een lijn? van J. van de Craats.
Na anderhalve eeuw is dit vermoeden, dat ook wel bekend staat als de Riemannhypothese, nog steeds niet opgelost. Het vormt zonder twijfel een van de belangrijkste problemen uit de moderne wiskunde. Vandaag de dag is de hypothese met computers gecheckt tot in de biljoenen nulpunten, maar een formeel bewijs is nog steeds niet gevonden.
Na verwoede pogingen van generaties aan wiskundigen heeft het vraagstuk zich verassend genoeg ook naar de natuurkunde verplaatst. Er blijkt namelijk een interessant verband te zijn tussen de nulpunten van de zètafunctie en de quantumfysica. Wellicht kan deze nieuwe benadering helpen bij het vinden van een bewijs van Riemanns vermoeden.
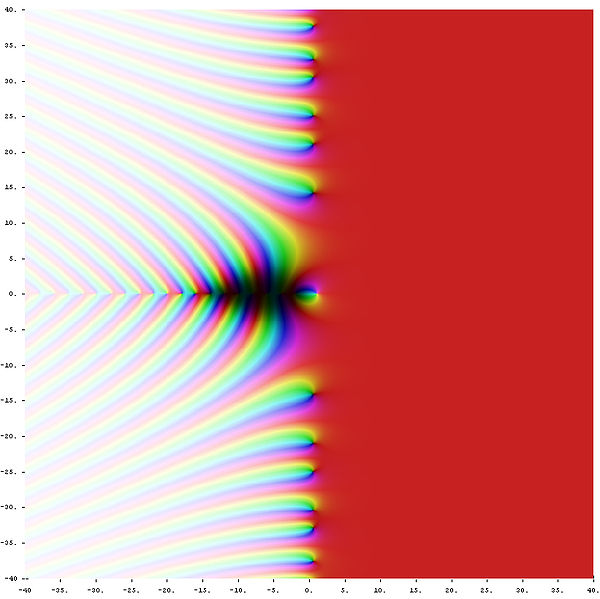
Afbeelding 3. Een ‘bovenaanzicht’ van de zetafunctie.De kleuren en intensiteit geven grofweg aan hoe hoog de grafiek is boven ieder punt in het vlak. Vergelijk dit eens met afbeelding 2: kun je zien waar de nulpunten liggen? Afbeelding: Jan Homann.
Het Hilbert-Pólyavermoeden
In het begin van 1914 was George Pólya, een Hongaarse wiskundige, in Göttingen om zich als student van Edmund Landau te verdiepen in de getaltheorie. Op een dag vroeg Landau hem: “Jij weet wat van natuurkunde af. Kun je een natuurkundige reden bedenken waarom de Riemannhypothese waar zou kunnen zijn?” Pólya kwam met het volgende idee: stel je voor dat er een natuurkundig quantummechanisch systeem bestaat waarvan de energieniveaus (de mogelijke energieën, dus) een verband hebben met de nulpunten van de zètafunctie. De energieën En komen in dit hypothetische systeem overeen met nulpunten van de vorm
sn = ½ + i En.
Het bestaan van zo’n systeem zou dan direct de Riemannhypothese bewijzen! Dit komt doordat de energieën van een natuurkundig systeem altijd reëel zijn – het zijn immers getallen die je kunt waarnemen in een experiment. Het is dus niet mogelijk dat een imaginair deel van de energie, vermenigvuldigd met i, bijdraagt aan het reële deel van de sn. Om deze reden hebben de nulpunten altijd een reëel deel gelijk aan ½, en dat is precies wat de Riemann-hypothese zegt. Het bovenstaande argument kwam bekend te staan als het Hilbert-Pólyavermoeden – hoewel Hilberts betrokkenheid in het vermoeden niet helemaal duidelijk is. De vraag is nu natuurlijk of we een dergelijk quantumsysteem ook daadwerkelijk kunnen bedenken. Het duurde tot de jaren 70 voordat het Hilbert-Pólya vermoeden opnieuw opdook, en wel in de context van toevalsmatrices.

Afbeelding 4. De brief van Pólya.Brief van George Pólya aan zijn collega Andrew Odlyzko waarin hij zijn gesprek met Edmund Landau beschrijft. Bron: Correspondence about the origins of the Hilbert-Polya Conjecture.
Een toevallige ontmoeting
Hugh Montgomery was een van de wiskundigen die zich in de jaren 70 bezighield met de nulpunten van de zètafunctie. In April 1972 bezocht hij het Institute for Advanced Study in Princeton om zijn resultaten te delen. Montgomery had ontdekt dat de statistische verdeling van de nulpunten een opmerkelijke eigenschap vertoonde, namelijk dat de nulpunten de neiging hebben elkaar ‘af te stoten’. Tijdens een toevallige ontmoeting vertelde hij dit, onder het genot van een kopje thee, aan Freeman Dyson, een professor aan het instituut.
Freeman Dyson, een Amerikaanse theoretisch natuurkundige, was in de jaren 60 een van de belangrijkste figuren in het onderzoek naar toevalsmatrices. Zoals we al eerder bespraken werden toevalsmatrices voor het eerst gebruikt door Eugene Wigner om het schijnbaar chaotische gedrag van de energieniveaus van zware atoomkernen te verklaren. Mede door het werk van Dyson was de statistische verdeling van de eigenwaarden van deze toevalsmatrices aan het einde van de jaren 60 grotendeels begrepen. Na het theetijdgesprek zag Dyson direct in dat de statistische verdeling die Montgomery ontdekt had exact overeenkwam met de verdeling die hij een tiental jaar geleden in zijn onderzoek naar toevalsmatrices had gevonden.
De onverwachte ontdekking door Montgomery en Dyson dat de nulpunten van de zètafunctie en de eigenwaarden van toevalsmatrices door dezelfde statistiek worden bepaald, wijst op een diep verband tussen priemgetallen en natuurkunde. Er is sindsdien veel onderzoek gedaan om dit verband beter te begrijpen. Om te beginnen heeft Andrew Odlyzko in 1989 zo’n miljoen nulpunten berekend en laten zien dat hun verdeling inderdaad precies overeenkomt met die van bepaalde toevalsmatrices. Daarnaast geeft de introductie van toevalsmatrices een nieuwe interpretatie aan het Hilbert-Pólyavermoeden: het quantumsysteem waar we naar op zoek zijn, moet chaotisch gedrag vertonen en door een toevalsmatrix kunnen worden beschreven. De afgelopen jaren zijn er veel van dit soort systemen voorgesteld en bestudeerd, maar tot nu toe heeft dit nog niet geleid tot een definitief bewijs van het vermoeden. De mogelijkheden zijn echter nog lang niet uitgeput, en toevalsmatrices worden nog steeds gezien als een veelbelovende aanpak om uiteindelijk tot een bewijs van de Riemannhypothese te komen.
Met die hoopgevende gedachte eindigen we ons laatste artikel in het drieluik over de toepassingen van toevalsmatrices binnen de natuurkunde. De grote vraag die blijft hangen is waarom zoveel compleet verschillende processen binnen de natuurkunde en de wiskunde, van zware atoomkernen tot nulpunten van de zètafunctie, een goede beschrijving vinden in toevalsmatrices. Wat is het achterliggende principe dat voor deze verbanden zorgt? Net als bij de derde Matrixfilm is dit einde misschien wat onbevredigend. We kunnen daarom alleen maar hopen dat er in het onderzoek naar toevalsmatrices, net als bij de films, binnenkort een vervolg uitkomt.
Bronnen
B. Riemann (1859),“Über die Anzahl der Primzahlen unter einer gegebenen Grösse” Monatsberichte der Berliner Akademie.In Gesammelte Werke, Teubner, Leipzig (1892).
H. L. Montgomery, “The pair correlation of zeros of the zeta function,” Analytic Number Theory, Proc. Sympos. Pure Math. XXIV (1973) 181–193.
A. M. Odlyzko, “On the distribution of spacings between zeros of the zeta function,” Math. Comp. 48 (1987) 273–308.
Verder lezen
https://www.quantamagazine.org/quantum-physicists-attack-the-riemann-hypothesis-20170404