
Figuur 1. Sterrenstelsels in de BeeldhouwerSterrenstelsels behoren tot de grootste objecten in het heelal. Veel sterrenstelsels hebben een doorsnede die, in meters uitgedrukt, een getal van zo’n twintig cijfers is. (Op deze foto de sterrenstelsels 2MASX J00482185-2507365 in het sterrenbeeld Beeldhouwer. Foto: NASA.)
Om zulke extreme getallen weer te geven, is het handig om ze uit te drukken in termen van een macht van tien. Het getal tien zelf noemen we de eerste macht van tien – ook wel geschreven als 101. De tweede macht van tien, geschreven als 102, is tien maal tien, dus honderd. De derde macht van tien, 103, is tien maal tien maal tien, dus duizend, enzovoort.
Niet elk getal is natuurlijk precies een hele macht van tien. Wel kunnen we elk getal uitdrukken in een “nabije macht”. 3700 kunnen we dus bijvoorbeeld schrijven als 3,7 x 103, of als 0,37 x 104. In dezelfde notatie is de straal van ons sterrenstelsel ongeveer 1,1 x 1021 meter. Een dergelijke notatie heeft twee voordelen:
- De schrijfwijze is veel compacter.
- Cijfers die geen betekenis hebben, hoeven niet te worden weergegeven. De leeftijd van het heelal is bijvoorbeeld ongeveer 13,7 x 109 jaar. Niemand weet precies of die leeftijd 13.700.000.000 jaar is, of bijvoorbeeld 13.732.167.994 jaar. Het heeft dus ook weinig zin om al die extra decimalen op te schrijven.
Negatieve machten geven getallen aan die kleiner zijn dan één. Tien tot de min-eerste macht is een tiende, tien tot de min-tweede macht een honderdste, enzovoort. In die notatie is de massa van het elektron ongeveer 9,1 x 10-31 kilogram.
We hebben nu positieve en negatieve machten van tien beschreven, maar hoeveel is eigenlijk tien tot de nulde macht? Wat nadenken leert dat er maar één logisch antwoord op die vraag is. Kijk bijvoorbeeld eens naar het getal 6375. De cijfers in dat getal betekenen het volgende: zes maal duizend, plus drie maal honderd, plus zeven maal tien, plus vijf maal één. Oftewel: zes maal 103, plus drie maal 102, plus zeven maal 101, plus vijf maal… wat? Het moge duidelijk zijn dat 100 het logische vervolg van de reeks is. We ontdekken zo dus dat 100 gelijk is aan 1.
Logaritmes
Omgekeerd kunnen we ons afvragen: welke macht van tien moeten we nemen om een bepaald getal te vinden? Die macht wordt de 10-logaritme van het getal genoemd. De 10-logaritme van 100 is dus 2, de 10-logaritme van 100.000 is 5, en de 10-logaritme van één miljoenste is -6.
Deze definitie van het logaritme kan worden uitgebreid tot getallen die tussen twee machten van 10 in liggen. Om te begrijpen hoe dat werkt, merken we eerst het volgende op. 103 (duizend) maal 102 (honderd) is 105 (honderdduizend). 104 (tienduizend) maal 105 (honderdduizend) is 109 (een miljard). We zien hier de volgende regelmaat: als we twee getallen vermenigvuldigen, tellen de logaritmen op.
Ervan uitgaande dat die regel ook geldt voor niet-gehele machten, leren we dat 100,5 maal 100,5 gelijk zou moeten zijn aan 101 (tien). Met andere woorden: 100,5 is de wortel van 10 – ongeveer 3,16. Of omgekeerd gezegd: de 10-logaritme van 3,16 is 0,5. Op een soortgelijke manier kunnen we van elk getal een 10-logaritme berekenen, al wordt het rekenwerk natuurlijk al snel heel lastig, en kunnen we dat beter aan een rekenmachine of computer overlaten. Zo vinden we bijvoorbeeld dat de 10-logaritme van 3700 ongeveer gelijk is aan 3,57. De orde van grootte van dat antwoord zou ons niet moeten verbazen: 3700 is meer dan 103 en minder dan 104, dus de logaritme moet ergens tussen 3 en 4 in liggen.
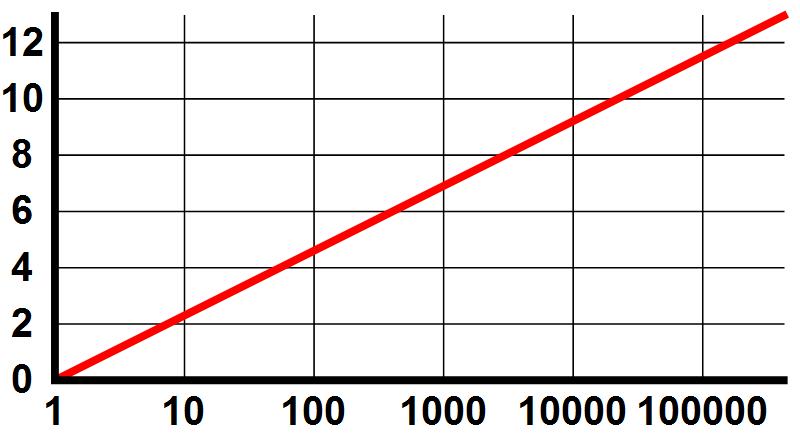
Figuur 2. Een logaritmegrafiekLogaritmes uitgezet in een grafiek: horizontaal het getal waarvan we de logaritme nemen, verticaal de e-logaritme. We zien dat ook van grote getallen de logaritme nog een betrekkelijk klein getal is.
Natuurlijk is er niets bijzonders aan het getal 10, behalve dan dat wij toevallig tien vingers aan onze handen hebben. We hadden ook kunnen vragen welke macht van 2 een bepaald getal is, en zo de 2-logaritme kunnen definiëren. De 2-logaritme van 8 is bijvoorbeeld 3, de 2-logaritme van 1/16 is -4.
Natuurkundigen werken graag met de e-logaritme, waarbij e de naam is van een getal dat ongeveer 2,72 is. De reden hiervoor is dat het gebruik van de e-logaritme veel rekenwerk vereenvoudigt. Een goede vuistregel is dat de e-logaritme van een getal zo’n 2,3 maal groter is dan de 10-logaritme; de e-logaritme van 10 is dus ongeveer 2,3; de e-logaritme van 1000 is ongeveer 3 x 2,3 = 6,9, enzovoort. De e-logaritme wordt in de natuurkunde zo vaak gebruikt dat de e-logaritme ook wel de “natuurlijke logaritme” wordt genoemd, en vaak wordt aangegeven zonder het voorvoegsel “e”. (Daarmee wijkt de wetenschappelijke notatie iets af van de notatie in veel schoolboeken, waar “log” wordt geschreven voor de 10-logaritme, en “ln” voor de e-logaritme.)
Om een indruk te krijgen van logaritmes volgt hieronder een tabel van logaritmes van een aantal getallen:
Getal | 10-log | 2-log | (e-) log |
1 | 0 | 0 | 0 |
2 | 0,30 | 1 | 0,69 |
4 | 0,60 | 2 | 1,39 |
10 | 1 | 3,32 | 2,30 |
100 | 2 | 6,64 | 4,61 |
1000 | 3 | 9,97 | 6,91 |
1024 | 3,01 | 10 | 6,93 |
6482934167892 | 12,81 | 42,56 | 29,50 |
Alle getallen met decimalen achter de komma zijn afrondingen: de logaritmes van de meeste getallen hebben oneindig veel getallen achter de komma. Het (willekeurig gekozen) voorbeeld in de laatste rij laat een belangrijke eigenschap van logaritmes zien: zelfs van heel grote getallen is een logaritme vaak nog betrekkelijk klein. De reden daarvoor is dat een logaritme iets zegt over de lengte van een getal: de 10-logaritme telt bijvoorbeeld grofweg het aantal cijfers van een getal in ons gebruikelijke, tientallige stelsel.
Wie van puzzelen houdt, ontdekt al snel de nodige regelmaat in de bovenstaande tabel. Het is een leuke uitdaging om de diverse vormen van regelmaat precies te formuleren, en te proberen te begrijpen wat de oorsprong ervan is. Dit leidt tot handige rekenregels voor logaritmes, die met wat oefening het schatten van een logaritme betrekkelijk eenvoudig maken.