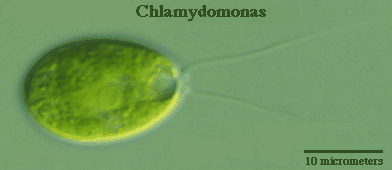
Afbeelding 1. Chalydomonas.De algensoort Chalydomonas reinhardtii kan zwemmen door een soort borstslag uit te voeren met twee lange dunne armen (flagella). Afbeelding: Rice University.
De Stokesvergelijking
Zoals we in het vorige artikel hebben gezien, worden vloeistofstromen nauwkeurig beschreven door de Navier-Stokesvergelijkingen, die een krachtenbalans uitdrukken tussen de traagheidskrachten en de wrijvingskrachten op een vloeistofelement. De sterkte van deze twee effecten wordt vergeleken door het Reynoldsgetal. Zoals we gezien hebben is dit Reynoldsgetal zeer klein voor de vloeistofstromen die een rol spelen bij zwemmen op microschaal, en dus kunnen we de traagheidseffecten in dat geval verwaarlozen. Wanneer we deze traagheidseffecten weglaten uit de Navier-Stokesvergelijking, vinden we de zogenaamde Stokesvergelijking, die nu alleen een krachtenbalans uitdrukt voor de wrijvingskrachten. In zijn volle glorie ziet de Stokesvergelijking er als volgt uit:
![]()
Wanneer we deze versimpelde vergelijking contrasteren met de oorspronkelijke Navier-Stokesvergelijkingen (zie het vorige artikel), valt meteen een belangrijk verschil op: de tijdsafhankelijkheid t is volledig uit de vergelijking verdwenen! Dit heeft een belangrijk gevolg voor zwemmen op microschaal, zoals we hieronder zullen zien.
De Schelpstelling
Laten we eens goed bekijken wat het betekent om op microschaal te zwemmen. Zwemmen betekent jezelf in een vloeistof voortstuwen door het uitvoeren van een zwemslag: een periodieke verandering van lichaamsvorm. Na zo’n slag-cyclus ben je weer terug in de oorspronkelijke vorm, maar (hopelijk) een beetje verplaatst als gevolg van de zwemslag. Door deze cyclus vaak te herhalen, kom je vooruit.
Bij zwemmen op microschaal is het Reynoldsgetal klein en worden de vloeistofstromen dus beschreven door de Stokesvergelijking hierboven. Zoals we zagen, bevat deze vergelijking geen tijdsafhankelijkheid meer. Als gevolg hiervan hangt de verplaatsing per slag van een zwemmer alleen af van het zwemslagpatroon, de reeks van de vormen die de zwemmer aanneemt tijdens de cyclus, maar is die verplaatsing onafhankelijk van de vraag of deze zwemslag snel of langzaam wordt uitgevoerd. Bovendien: wanneer dit patroon wordt omgekeerd, gaat de zwemmer dus de andere kant op!
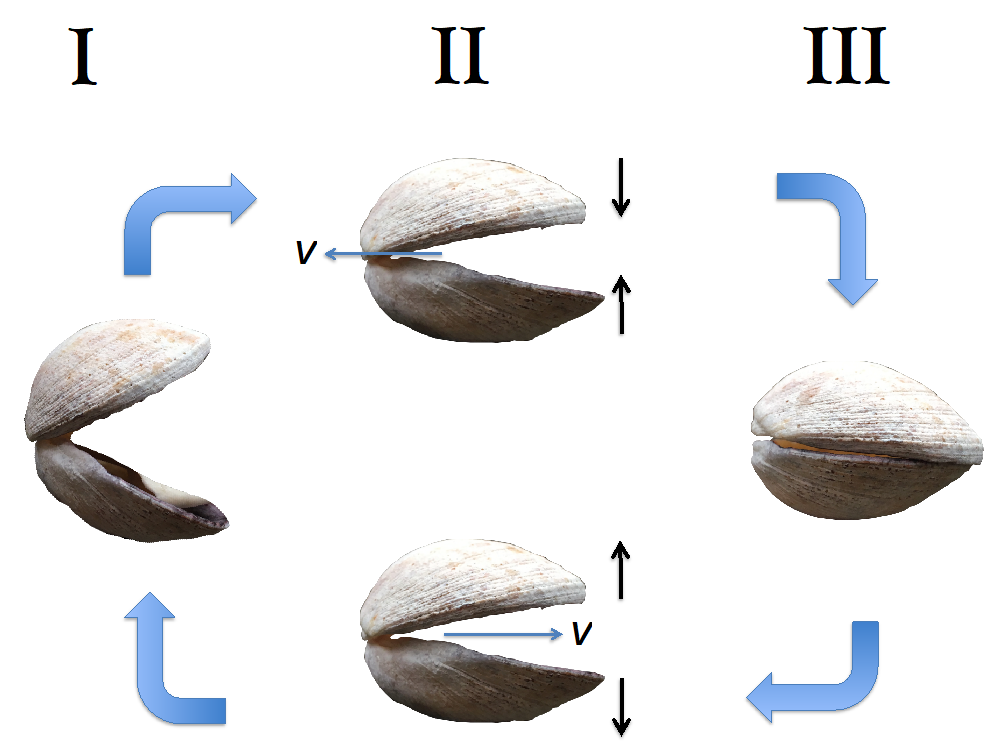
Afbeelding 2. Een zwemmende schelp.De zwemcyclus van een schelp. De schelp gaat vooruit (v>0) door dicht te klappen (figuur I – III). Bij het openklappen (figuur III –I), doorloopt de schelp dezelfde stappen in omgekeerde volgorde. Omdat traagheid verwaarloosbaar is op microschaal, kan een microscopisch kleine schelp dus niet zwemmen. Afbeelding uit het proefschrift van de auteur.
Om in te zien wat het effect van een verwaarloosbare traagheid is op het zwemmen, kijken we eerst naar het zwemgedrag van een hele simpele zwemmer: een schelp. Een schelp gaat vooruit door het dichtklappen van de schelp (figuur I-III in afbeelding 2). Bij het openklappen doorloopt de schelp echter precies dezelfde stappen als bij het dichtklappen, maar in de omgekeerde volgorde (III-I). Bij laag Reynoldsgetal zal de schelp dus bij de openslaande beweging even ver terug bewegen als zij bij het dichtklappen vooruit ging.
Een andere manier om dit te formuleren is dat de zwemslag I-III-I invariant is onder omkering van de tijd (“reversibel”): we kunnen op geen enkele manier uitmaken in welke richting de cyclus in afbeelding 2 door de schelp wordt doorlopen. Daarom kan zo’n zwemslag onmogelijk een netto verplaatsing opleveren. In zijn beroemde lezing “leven bij lage Reynoldsgetallen” vatte Edward Purcell dit principe samen in de zogenaamde Schelpstelling: een schelp kan niet zwemmen bij een laag Reynoldsgetal. Merk op dat een schelp maar een enkele vrijheidsgraad heeft (één scharnier) en dus wel een reversibele zwemslag móet maken. Het motto voor zwemmen op kleine schaal is dus: maak met minimaal twee vrijheidsgraden een niet-reversibele zwemslag!
Zwemles van Darwin
Om zwemslagen te construeren die aan de schelpstelling kunnen ontsnappen, kunnen we inspiratie putten uit de natuur. In de natuur wordt op microschaal gezwommen door allerlei organismen, met een enorme verscheidenheid aan vormen en zwemslagen. Grofweg kunnen we daar echter twee duidelijke categorieën in onderscheiden.
De eerste manier waarmee veelvuldig de schelpstelling wordt omzeild is door het gebruik van flexibele ledematen (flagella). Een goed voorbeeld hiervan is de alg Chlamydomonas reinhardtii, te zien in afbeelding 1 bovenaan dit artikel. Hieronder zie je een filmpje van de zwemmende alg:
Deze alg heeft twee flagella aan de voorkant, waarmee een soort borstslag wordt uitgevoerd: de flagella zijn uitgestrekt wanneer de alg zijn flagella naar achter duwt (en dus zichzelf naar voren), en gebogen wanneer de flagella weer naar voren gebracht moeten worden. Omdat de flagella een andere vorm aannemen bij de teruggaande beweging, is deze zwemslag niet-reversibel: we zouden het gemakkelijk kunnen zien wanneer het filmpje achterstevoren wordt afgespeeld. Door deze niet-omkeerbaarheid is de Chlamydomonas dus in staat om te zwemmen.
Een andere veelgebruikte zwemslag berust op het gebruik van helixvormige flagella. Een goed voorbeeld hiervan is de bacterie Escherichia coli, die een bundel van helixvormige flagella achter zich ronddraait als een soort propeller. Omdat een helix een intrinsieke draairichting (heliciteit) heeft, geeft het ronddraaien van zo’n helix een niet-reversible zwemslag en komt de E. coli vooruit:
Zwemmen op microschaal: lastiger, maar het kan!
We hebben gezien dat het ontbreken van traagheid tot gevolg heeft dat onze intuïtie over zwemmen niet opgaat op micrometerschaal – iets wat wordt samengevat in de Schelpstelling. Die stelling maakt zwemmen op micrometerschaal een stuk lastiger, maar de natuur leert ons gelukkig dat zwemmen door stroperig-lijkende vloeistoffen toch op allerlei manieren mogelijk is. Het interessante onderzoek naar al deze verschillende zwemmogelijkheden (en hun eventuele toepassingen) is nog in volle gang.