De naam ‘caleidoscoop’ is samengesteld uit drie woorden in het oud Grieks: καλός (kalos), “mooi, schoonheid”, εἶδος (eidos), “vorm” en σκοπέω (skopeō), “kijken naar, onderzoeken”. Samen betekent de naam dus iets als “(instrument voor de) waarneming van mooie vormen.” De caleidoscoop werd uitgevonden en gepatenteerd door de wetenschapper (en “vader van de moderne experimentele optica”) Sir David Brewster in 1817.
Wat je ziet in een caleidoscoop zijn mooie, vaak duizelingwekkende patronen, gemaakt door een slim gebruik van spiegels. De aantrekkingskracht van de patronen die je ziet komt door de intrinsieke schoonheid van symmetrie, iets wat je in de natuurkunde wel vaker tegenkomt. Symmetrieën spelen een centrale rol in het standaardmodel van de deeltjesfysica, in vaste stoffen, bij de vraag of je kunt zitten op een stoel, en eigenlijk voor alles daartussenin.
Anatomie van een caleidoscoop
In afbeelding 1, hieronder, zie je hoe de simpele combinatie van twee spiegels het beeld van een enkel object rond kan draaien. Zo wordt een munt omgetoverd in een cirkel van munten, met als middelpunt de hoek waar de twee spiegels samenkomen. De hoek (θ) tussen de twee spiegels is belangrijk: je krijgt alleen een mooi patroon wanneer 360/θ gelijk is aan een even geheel getal. Zo zou je bijvoorbeeld hoeken van 90, 60, 45, 30, 22,5, 15, … graden kunnen gebruiken. Alleen als de hoek precies goed is, komen de twee gereflecteerde plaatjes aan de tegenovergestelde kant van de cirkel als het echte object precies overeen. Probeer het zelf maar eens!
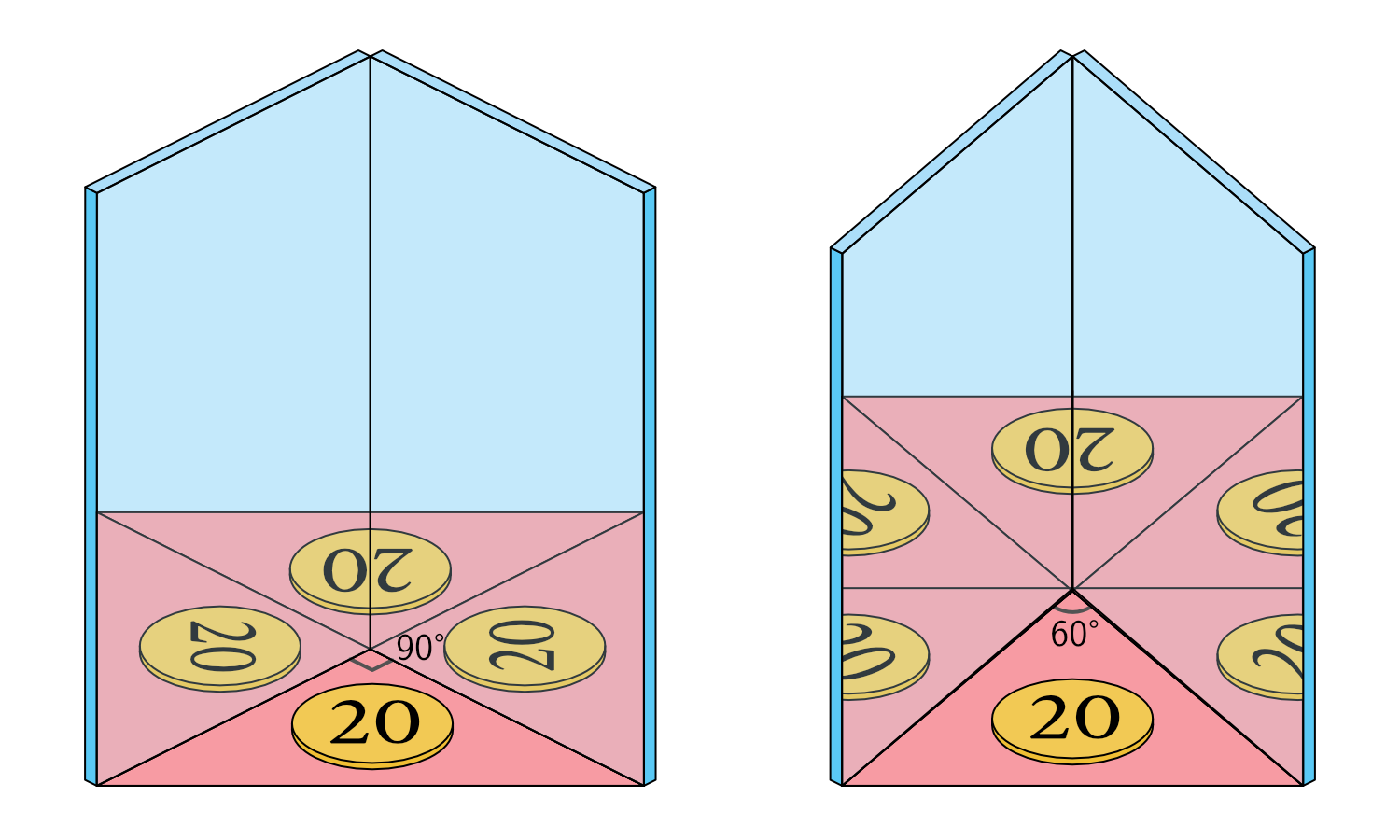
Deze regel voor de hoek θ is precies de truc waar Brewster achter was gekomen. Natuurlijk werkt de truc niet alleen met een enkel object, maar met alles wat je tussen de twee spiegels in zet. Stop de spiegels vervolgens in een lichtdichte buis, en je hebt een (simpele) caleidoscoop gebouwd – zie afbeelding 2.
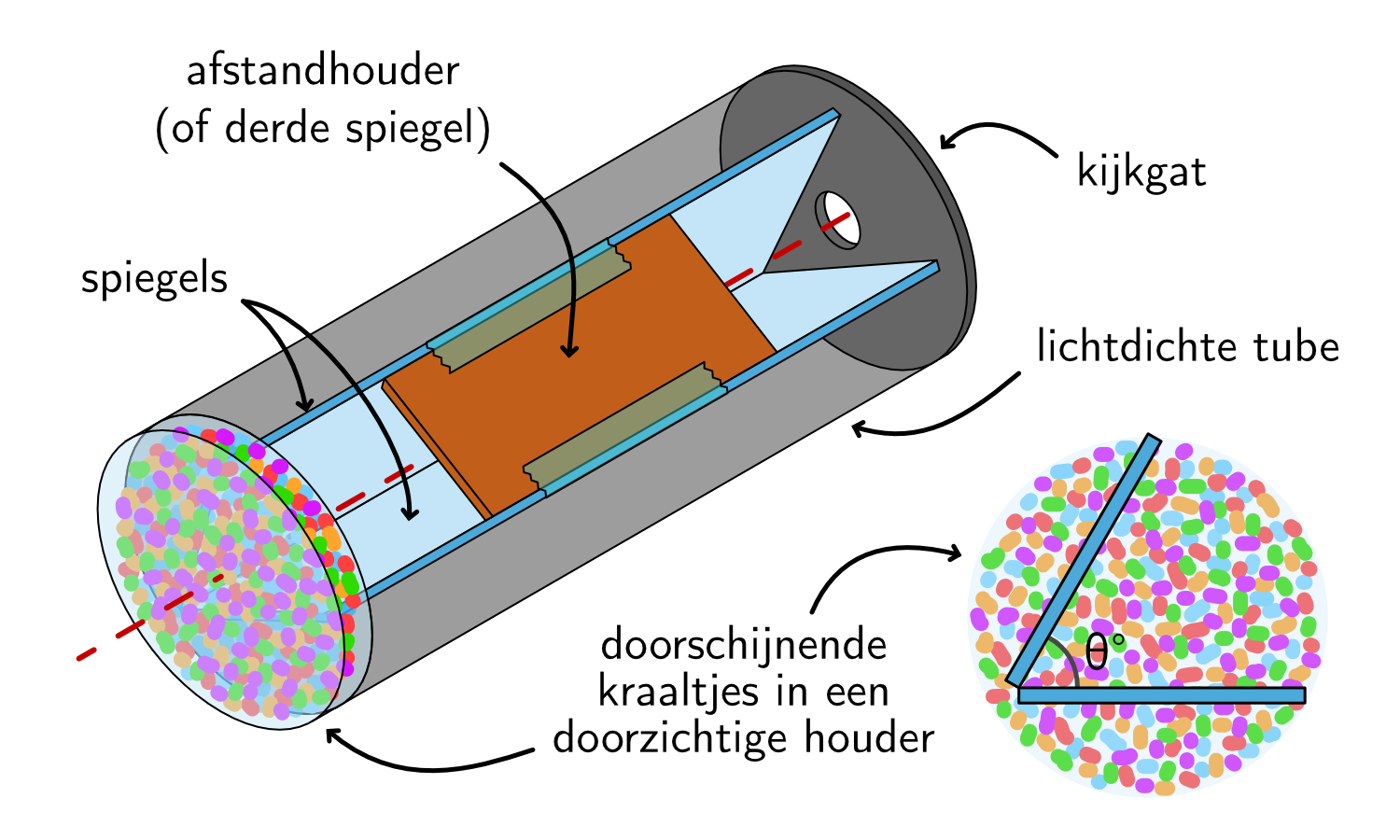
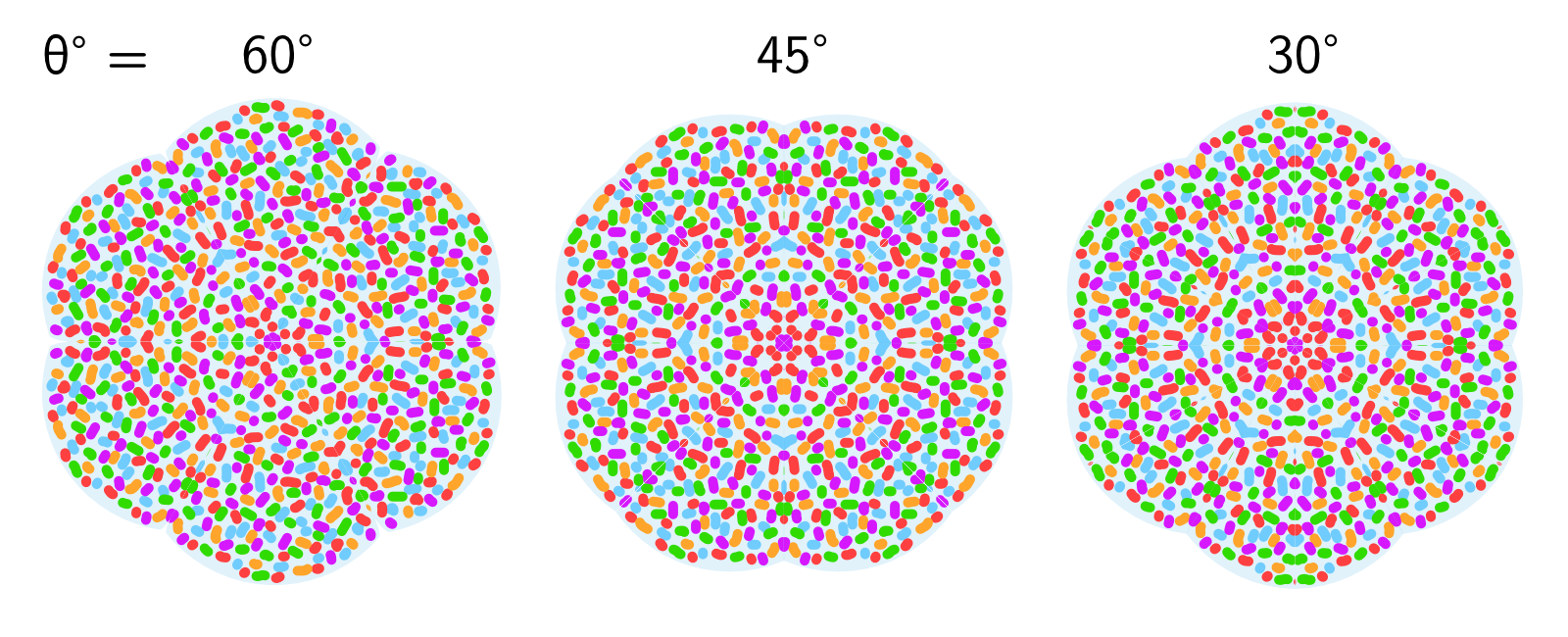
Als je aan het eind van de buis doorschijnende kraaltjes (of stukjes glas of plastic) in een doorzichtige houder stopt, krijg je al snel een interessant patroon. En dit werkt natuurlijk nog beter als de kraaltjes een beetje kunnen bewegen, dan kun je eindeloos veel patronen creëren door de buis rond te draaien of te schudden. De patronen zullen een beetje lijken op mandala’s, zoals je kunt zien in afbeelding 3.
Ad infinitum
Als je ooit zelf door een caleidoscoop gekeken hebt, is je misschien opgevallen dat het patroon dat je ziet niet zomaar ophoudt na één draaiing. Dat komt omdat de meeste caleidoscopen niet twee, maar dríe spiegels gebruiken. Door met drie spiegels een gelijkzijdige driehoek (θ = 60°) te construeren, blijft het patroon zich eindeloos herhalen – ad infinitum! Kun je in de voorbeelden in afbeelding 4 zien welke driehoek de oorsprong is van alle reflecties? Hij is misschien kleiner dan je denkt!

Je zou in plaats van een gelijkzijdige driehoek ook andere hoeken kunnen gebruiken, en/of meer spiegels. Brewster presenteert in zijn boek Treatise on the kaleidoscope (‘Verhandeling over de caleidoscoop,’ 1819) veel interessante configuraties, waarvan je er enkele ziet in afbeelding 5. Ook een leuk feitje: door een gelijkzijdige veelhoek van spiegels in elkaar te knutselen kun je niet alleen tweedimensionale patronen creëren, maar ook driedimensionale platonische lichamen! Benieuwd? Zie dan deze link. Ben je nu ook overtuigd van de schoonheid van symmetrie?