
Je zou verwachten dat ieder cijfer met kans 1/9 het begincijfer van een element uit de dataset is. Laten we het experiment uitvoeren met machten van 2. Onze verzameling bestaat dus uit de getallen 2,4,8,16,32, enzovoort. De verwachting is dat als een histogram met de begincijfers van de eerste duizend machten van 2, er vrij uniform uit zal zien, zoals is weergegeven in afbeelding 2.
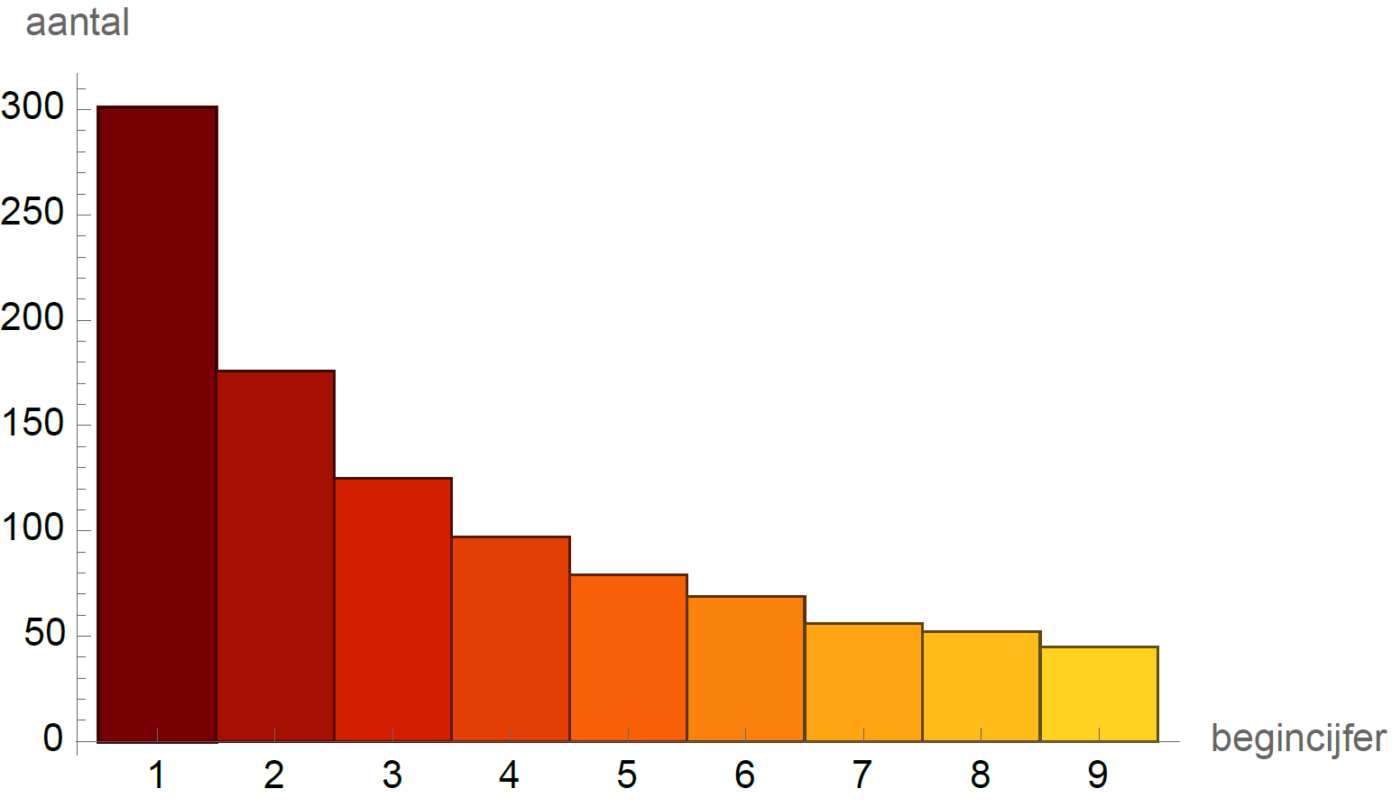
Hieronder, in afbeelding 3, laten we een histogram zien gemaakt met de daadwerkelijke begincijfers van de eerste duizend machten van 2.
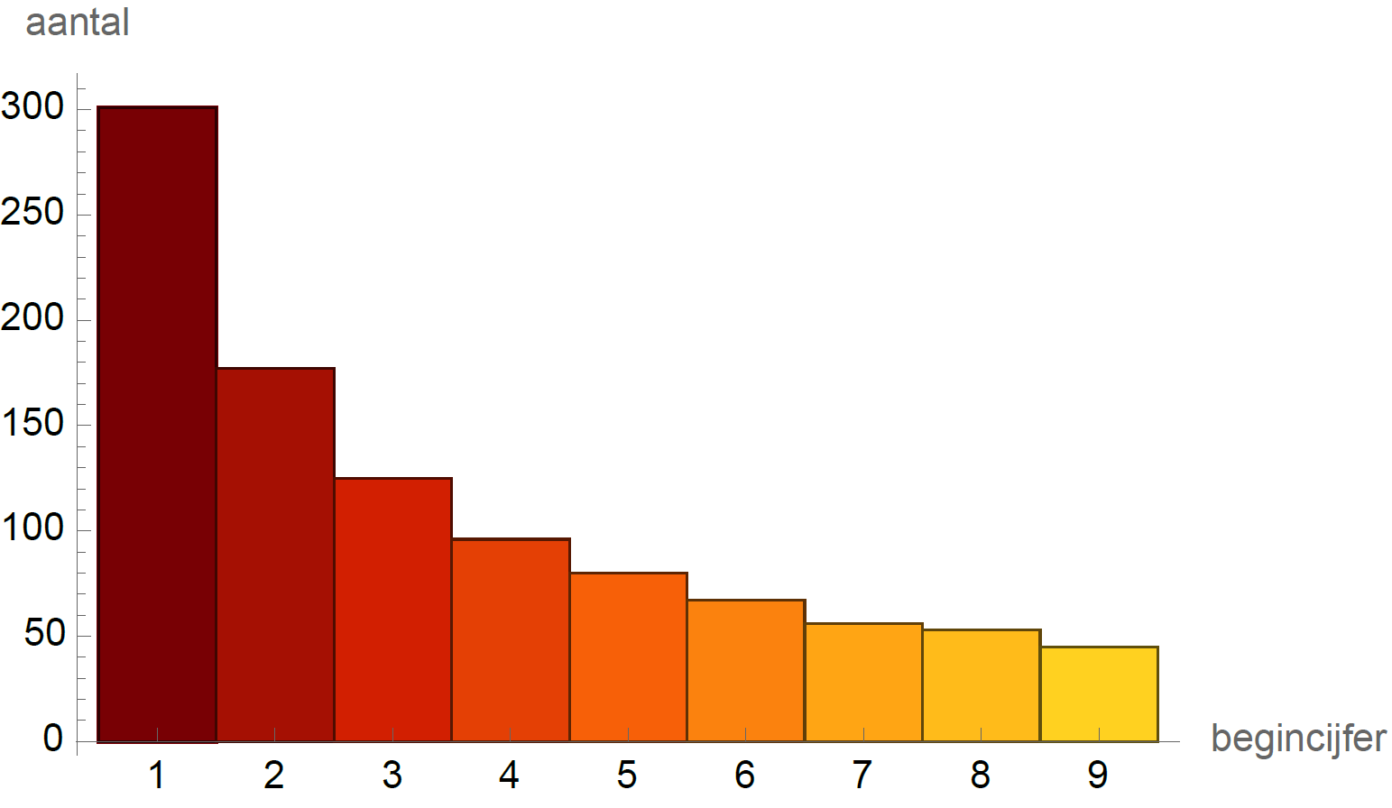
Onze verwachting lijkt toch niet te kloppen. Misschien zijn machten van 2 geen goede dataset? Een andere verzameling die meerdere orde van grootes omvat is de reeks van Fibonacci. De reeks van Fibonacci wordt gekenmerkt door het feit dat elk getal in de reeks de som is van de voorgaande twee. We nemen weer de eerste duizend getallen in de reeks en maken een histogram, weergegeven in afbeelding 4. En wat blijkt? De verdeling van begincijfers ziet er vrijwel hetzelfde uit als de verdeling voor machten van 2!
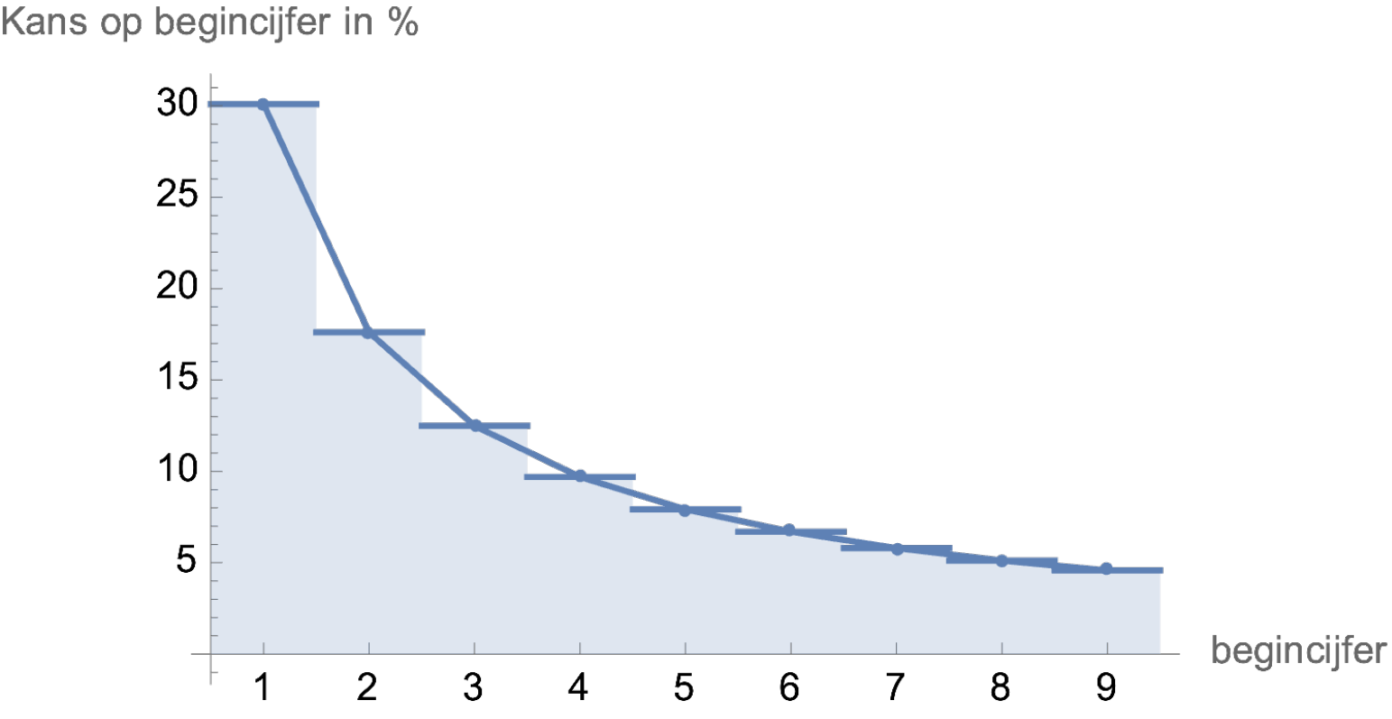
Het volgende patroon komt naar voren: het begincijfer 1 komt vaker voor dan 2, en 2 komt weer vaker voor dan 3, enzovoort. De begincijfers volgen de zogenaamde wet van Benford. Die wet zegt het volgende: het begincijfer 1 komt ongeveer 30% van de tijd voor, terwijl 2 slechts 18% van de tijd voorkomt, en zo door tot het cijfer 9 dat zelfs minder dan 5% van de tijd voorkomt. De precieze verdeling is gegeven door de volgende formule:
Kans op begincijfer \( d = \log_{10} \left( 1 + \frac{1}{d} \right) \),
en de verdeling ziet er uit als weergegeven in afbeelding 5.
Zoals je misschien al raadt volgen niet alleen machten van 2 en de Fibonaccireeks de wet van Benford. Bijna iedere verzameling getallen die een aantal ordes van grootte omvat volgt die wet. Voorbeelden zijn de inwonersaantallen van steden in Europa, beurskoersen, en de lengte van rivieren. De reden waarom zoveel verzamelingen de wet van Benford volgen is echter een raadsel.
De wiskundigen onder jullie zullen misschien denken: dit moet iets met eenheden te maken hebben! Makkelijk te controleren is dat het voor de lijst van natuurconstanten voor de verdeling niet uitmaakt in welke eenheden de constanten zijn uitgedrukt. Ook voor andere verzamelingen getallen met eenheden lijkt het niet uit te maken of we die in kilometers, mijlen of lichtjaren meten. Toch zul je misschien nog steeds een bezwaar maken dat te maken heeft met eenheden. We “meten” onze getallen namelijk in grondtal 10. Als we een getal in grondtal 10 bekijken, bijvoorbeeld een viercijferig getal \( g_{10} = abcd \) dat opgebouwd is uit de cijfers \( a, b, c \) en \( d \), dan is het getal gelijk aan \( g_{10} = d \times 10^0 + c \times 10^1 + b \times 10^2 + a \times 10^3 \). Maar we kunnen getallen natuurlijk net zo goed in een ander grondtal meten. Neem als voorbeeld het getal \( g_{10} = 9876 \). In grondtal 7 is het getal dan \( g_{7} = 40536 \), want
\( 9876 = 4 \times 7^4 + 0 \times 7^3 + 5 \times 7^2 + 3 \times 7^1 + 6 \times 7^0 \).
Dit voorbeeld laat al zien dat de begincijfers van getallen flink afhangen van het grondtal waarin we de getallen meten. Laten we ons experiment nogmaals doen, maar nu met de eerste 1000 machten van 2 in grondtal 7. De verdeling die we dan vinden is weergegeven in afbeelding 6.
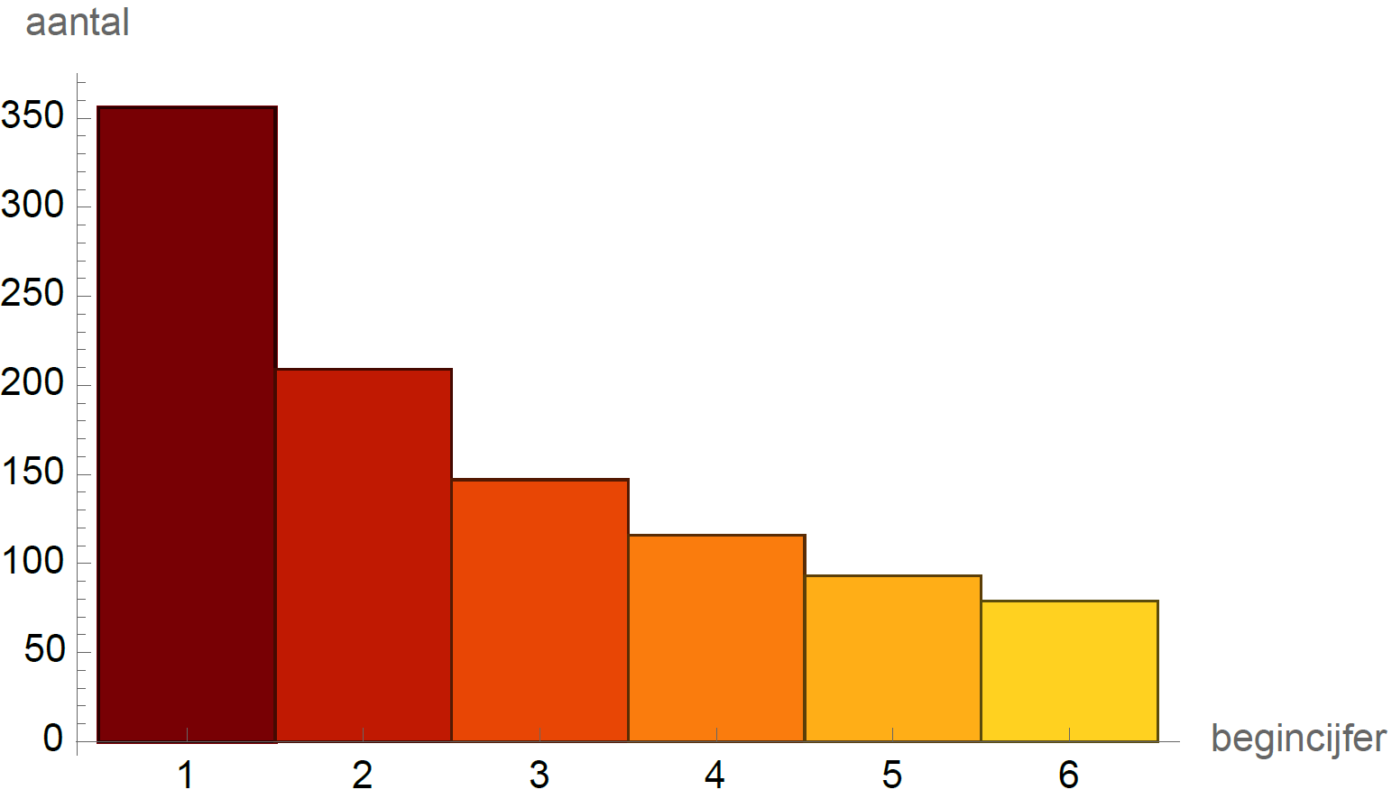
Nog steeds zijn de kansen op begincijfers niet uniform verdeeld. De begincijfers volgen, hoe kan het ook anders, Benford’s wet met grondtal 7. Deze kansverdeling is gegeven door
Kans op begincijfer \( d = \log_{7} \left( 1 + \frac{1}{d} \right) \).
Nu blijft de vraag natuurlijk: als het niet door de eenheden komt, waarom volgen getallen dan de wet van Benford? Na jaren puzzelen hebben veel wiskundigen de zoektocht naar een exact antwoord op deze vraag opgegeven. Warren Weaver, wiskundige en auteur van een boek over kansberekeningen “Lady Luck: The Theory of Probability” zei er in dat boek het volgende over:
“This fact, at first so strange that I have known very able mathematicians initially to pooh-pooh the idea, is simply an inherent characteristic of our decimal number system.”
Kort gezegd: de wet van Benford, is niet te verklaren en zit ingebakken in het getallenstelsel. Dat wil niet zeggen dat wiskundigen niet hebben geprobeerd een verklaring te vinden. Een idee is dat het fenomeen te maken heeft met schaalinvariantie: als de begincijfers van een verzameling een bepaalde universele verdeling volgen, dan moet die verdeling onafhankelijk zijn van de eenheden waarin we die getallen meten. Onder deze veronderstelling is het mogelijk om de wet van Benford af te leiden. Er zit echter een addertje onder het gras. Om het bewijs voltooien moet je ervan uitgaan dat er een universele verdeling bestaat, dus een verdeling die niet afhangt van de details van de verzameling zodat (vrijwel) iedere verzameling eraan voldoet; iets dat helemaal niet vanzelfsprekend is. Een volledig bewijs zou dus moeten laten zien waarom er een universele verdeling zou bestaan voor grote verzamelingen van getallen.
De wet van Benford lijkt dus te gelden, maar er is geen bewijs. Misschien vraag je je af waar de wet dan nuttig voor is. Het blijkt echter dat de wet van Benford juist erg nuttig is. Als je namelijk weet dat grote datasets vaak een patroon volgen, kan je die datasets testen en zien of ze daadwerkelijk dat patroon volgen. Als het antwoord op die vraag nee is, is dat natuurlijk een klein beetje verdacht. Is je dataset dan wel een “natuurlijk” verkregen dataset?
De Amerikaanse belastingdienst, de IRS, gebruikt de wet van Benford bijvoorbeeld om belastingfraude op te sporen. Als je belastingaangifte de wet van Benford niet volgt is dat natuurlijk niet genoeg om te bewijzen dat er fraude in het spel is, maar het zal er wel voor zorgen dat de accountants iets beter naar de getallen zullen kijken. Andere voorbeelden waarin de wet van Benford wordt gebruikt is het testen van datasets die gebruikt worden voor wetenschappelijk onderzoek, of om verkiezingsfraude op te sporen – iets dat de laatste jaren een hot topic is.
De wet van Benford werd bijvoorbeeld door Westerse landen gebruikt als bewijs voor grootschalige fraude bij de verkiezingen die in 2009 in Iran plaatsvonden. Daarnaast claimden aanhangers van voormalig president Donald Trump dat er in 2020 met verkiezingsdata uit enkele districten rond onder andere Chicago en Milwaukee gefraudeerd was, omdat de data de wet van Benford niet volgden. (De uitslagen uit de betreffende districten was niet erg gunstig voor Trump.) De verklaring hiervoor bleek echter te zijn dat de getallen die werden gebruikt niet de vereiste meerdere orde van groottes bevatten. Dit kun je ook als volgt zien: als er in alle districten ongeveer duizend stemmen worden uitgebracht, in een verkiezing tussen twee uitkomsten, dan verwacht natuurlijk je dat de begincijfers van de uitkomsten vaker met een 4, 5, of 6 beginnen dan met een 1, en dat de wet van Benford dus niet geldt.
Al met al is de wet van Benford nog een groot mysterie, zonder hoop op een oplossing. Desalniettemin heeft de wet handige toepassingen. Daarnaast zorgde het testen van verzamelingen van getallen voor de auteur van dit artikel voor een verrassend amusante middag. 🙂