
Eerder schreef Pim van den Heuvel op de QU-website al over de eerste resultaten van het DESI-onderzoek. Ik vat de hoofdpunten hier nog eens samen. DESI staat voor Dark Energy Spectroscopic Instrument; het experiment is een telescoop die op de Kitt Peak in Arizona in de Verenigde Staten staat. DESI meet de locaties van vele miljoenen sterrenstelsels, en wetenschappers hebben als doel hiermee de uitdijing van het heelal te bestuderen.
Het huidige model van ons heelal, ΛCDM (Lambda Cold Dark Matter), beschrijft de evolutie van een heelal met daarin materie, straling en donkere energie. Al deze ingrediënten gedragen zich anders onder de uitdijing van het heelal en hebben omgekeerd ook hun uitwerking op diezelfde uitdijing. Hoe dit precies gebeurt, wordt beschreven aan de hand van de Friedmannvergelijking:
\((H(a)/H_0)^2 = \Omega_m a^{-3} + \Omega_r a^{-4} + \Omega_k a^{-2}+\Omega_\Lambda.\)
Laat ik uitleggen wat de verschillende ingrediënten van deze vergelijking betekenen. De schaalfactor \(a(t)\) beschrijft de uitdijing, en is vandaag de dag (per definitie) gelijk aan één. Lang geleden was het heelal veel kleiner, en lag de schaalfactor tussen 0 en 1, terwijl wordt verwacht dat in de toekomst de schaalfactor alleen maar toeneemt. De linkerkant van de Friendmannvergelijking beschrijft de de snelheid waarmee het heelal uitdijt in termen van de Hubbleparameter \(H(a)\), en \(H_0\) is de waarde van die Hubbleparameter nu. De Hubbleparameter hangt af van de schaalfactor volgens
\(H(a(t)) \equiv \frac{\dot{a}(t)}{a(t)}.\)
De rechterkant van de Friedmannvergelijking beschrijft de energiedichtheid van de verschillende ingrediënten van ons heelal en hoe ze zich gedragen onder invloed van de uitdijing. \(\Omega_m\) is de materiedichtheid vandaag de dag. Als de ruimte uitzet verdunt de materie door zich te verdelen over de (driedimensionale) uitzetting, en dus verandert de energiedichtheid van materie als \( \Omega_m a^{-3}\). \(\Omega_r\) beschrijft de energiedichtheid van straling, en die straling verdunt nog sneller dan materie – vandaar de factor \( a^{-4} \). \(\Omega_k\) beschrijft de kromming van de ruimtetijd, maar die is vrijwel nul en wordt ook vaak weggelaten in de Friedmannvergelijking van ons universum.
Tot slot hebben we de term \(\Omega_\Lambda\). Dit is donkere energie; een ingrediënt waarvan Einstein zich gedwongen zag het toe te voegen aan zijn algemene relativiteitstheorie, om ervoor te zorgen dat het heelal volgens de formules niet ineen zou storten onder de invloed van zwaartekracht – en om dus een statisch universum te kunnen beschrijven. Ons universum is zoals we tegenwoordig weten helemaal niet statisch, maar dit nam Einstein toendertijd wel aan. Een beroemde anekdote is dan ook dat Einstein de donkere energie zijn grootste blunder zou hebben genoemd. Toch bleek de kosmologische constante Λ, een andere naam voor de donkere energie, wel degelijk nodig om ons universum te kunnen beschrijven. Het universum zet namelijk steeds sneller uit, en om dit te kunnen beschrijven bleek het toch nodig om Λ toe te voegen aan de theorie. Λ wordt de kosmologische constante genoemd omdat – zoals al te zien in de Friedmannvergelijking – wordt aangenomen dat de energiedichtheid van Λ niet schaalt met de uitzetting van het heelal, en in die zin dus “constant” is.
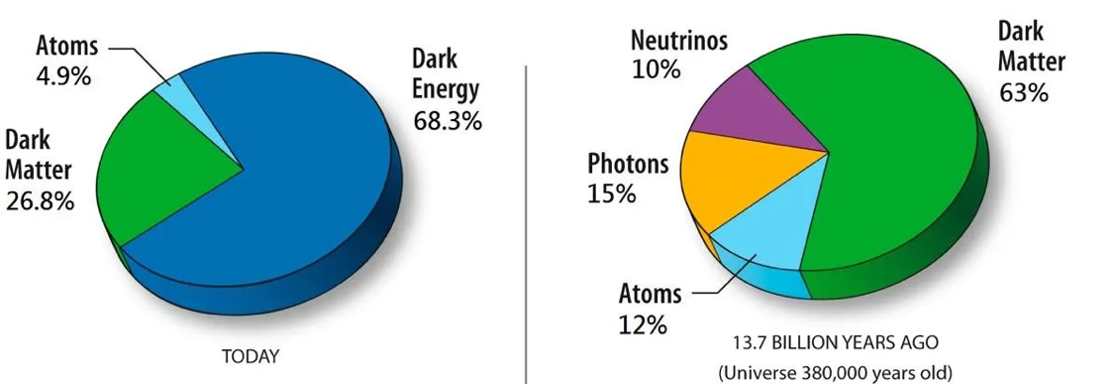
Dit is precies het gedrag dat wetenschappers met DESI wilden onderzoeken. Door nauwkeurig de positie van verschillende sterrenstelsels te bestuderen, kunnen we beter te weten komen hoe de uitdijing van het heelal zich gedurende de vele jaren heeft gedragen. Immers: het licht van een sterrenstelsel dat heel ver weg staat, bereikt ons pas na lange tijd; door heel ver het universum in te kijken, kijken we feitelijk terug de tijd in. Zo kan de evolutie van de uitdijing van het heelal in kaart gebracht worden. De wetenschappers in de DESI-samenwerking onderzoeken onder andere wat het model voorspelt als we niet aannemen dat de kosmologische constante echt constant is.
De afhankelijkheid van de energiedichtheid van een bepaalde vorm van “heelalvulling” als functie voor de schaalfactor wordt geparametriseerd door de bijbehorende toestandsvergelijking-parameter \(w\) volgens
\(\rho(a) = \rho_0 a^{-3(1+w)}.\)
In het ΛCDM-model wordt aangenomen dat bijvoorbeeld \(w=0\) voor materie, \(w=1/3\) voor straling en \( w=-1\) voor donkere energie. Je kunt zelf controleren dat die getallen inderdaad het gedrag van de termen aan de rechterkant van de Friedmannvergelijking hierboven reproduceren. De DESI-wetenschappers onderzoeken de mogelijkheid dat \(w\) voor donkere energie niet altijd exact gelijk is aan -1, maar dat die parameter afhankelijk is van de schaalfactor \( a \) zelf, en dus in de loop van de tijd verandert. Ze gebruiken de volgende aanname voor \(w\):
\(w(a) = w_0 + w_a (1-a).\)
De onderzoekers noemen dit het \(w_0 w_a\)CDM-model, als variant op ΛCDM, waarvoor \(w_0\) precies gelijk is aan -1 en \(w_a=0\).
Vorig jaar schreef Pim over de resultaten van het eerste jaar aan metingen van DESI, en twee maanden geleden werden de eerste drie jaar aan metingen gepubliceerd. De eerste metingen, beschreven in dit artikel, vonden dat waarden \(w_0>-1\) en \(w_a>0\) het meest consistent waren met de data. De gevonden resultaten weken af van ΛCDM met een nauwkeurigheid van tussen de 2,2 en 3,9 standaarddeviaties (of “sigma”), afhankelijk van welke datasets gecombineerd werden. In de wetenschappelijke wereld wordt gesproken van een ontdekking bij een nauwkeurigheid vanaf 5 sigma. Bij een nauwkeurigheid van 3 sigma is de kans dat de meting toevallig gedaan zou worden als het gemeten feit niet waar zou zijn al slechts 0,3 procent, maar het is vaker voorgekomen dat resultaten met 3 sigma significantie weer verdwijnen bij nauwkeurigere metingen. Een standaarddeviatie van 5 sigma betekent dat de kans dat de resultaten gevolg zijn van willekeurige fluctuaties slechts één op een miljoen is, en pas bij deze waarde spreekt de wetenschappelijke wereld echt van een ontdekking.
Wat hebben twee jaar extra aan metingen opgeleverd in het onderzoek naar de kosmologische constante? Een van de belangrijkste grafieken uit het artikel is hieronder weergegeven, en beschrijft de evolutie van de toestandsvergelijking-parameter \(w\) als functie van de roodverschuiving \(z\). De roodverschuiving van het licht van verre sterrenstelsels is een maat voor de schaalfactor die het heelal had op het moment waarnaar we terugkijken – en is gerelateerd aan die schaalfactor volgens \(a=(1+z)^{-1}\). “Vandaag” komt overeen met \(z=0\) en sterrenstelsels die ver weg staan, en waarvan het licht dus lang geleden is uitgezonden, corresponderen met hogere waardes van \(z\).
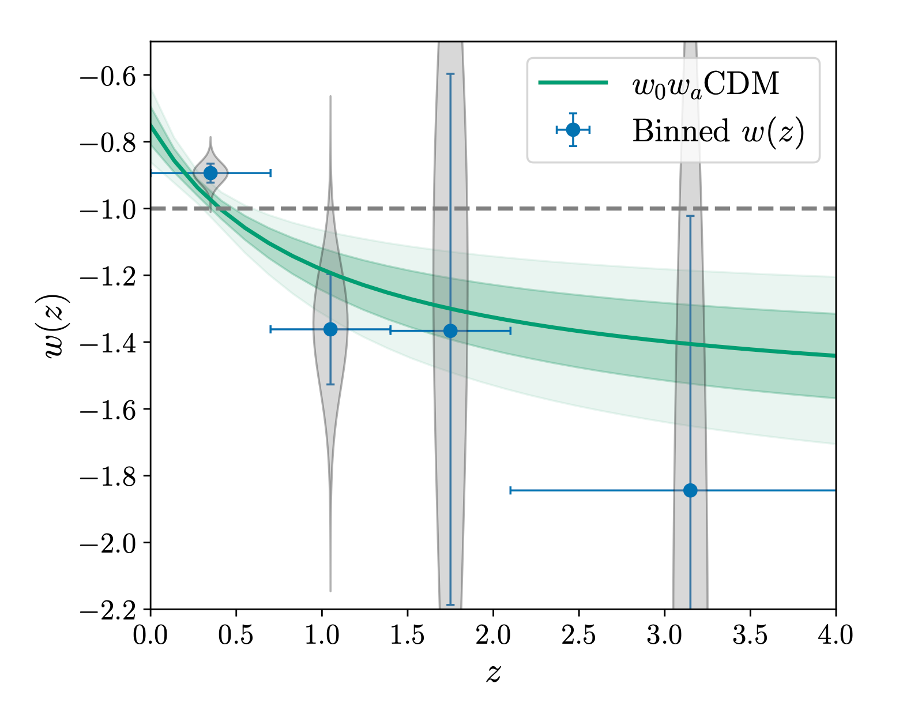
In de grafiek is een streepjeslijn getrokken op \(w(z)=-1\), de verwachting van ΛCDM, en de groene lijn beschrijft de best passende voorspelling volgens het \(w_0 w_a\)CDM-model. De blauwe stippen zijn de metingen. De wetenschappers vonden dus alweer dat de metingen beter bij \(w_0 w_a\)CDM aansluiten dan bij ΛCDM, wat suggereert dat de kosmologische constante misschien toch niet zo constant is. De huidige resultaten wijken af van ΛCDM met een nauwkeurigheid van 2,8 tot 4,2 sigma. Dit is dus een stuk nauwkeuriger dan de eerste publicatie van DESI, maar nog steeds onder de gouden standaard van 5 sigma.
Daarnaast – en dit is waar veel natuurkundigen zich zorgen over maken – is te zien dat de best passende lijn van het \(w_0 w_a\)CDM-model een toestandsvergelijking-parameter beschrijft die op hogere roodverschuiving een waarde aanneemt onder de -1. Dit breekt een aanname die voor veel natuurkundigen heel belangrijk is: de null energy condition (NEC), die inhoudt dat energiedichtheid nooit toeneemt als de ruimte uitzet.
Vanuit bijvoorbeeld de snaartheorie is het niet zo’n probleem als de kosmologische constante niet precies constant is: het is natuurkundigen juist zelfs nog niet gelukt om vanuit de snaartheorie een universum te beschrijven waarvoor dat wél zo is. Het blijkt misschien wel mogelijk te zijn om een situatie te krijgen waarin de kosmologische constante langzaam afneemt. Dit is eerder door Lars Aalsma besproken in dit artikel op onze website. Ook in deze theorie kan \(w\) overigens niet lager dan -1 zijn.
Kortom, de nieuwe DESI-metingen suggereren nog sterker dan eerst dat de kosmologische constante niet echt constant is, maar afneemt in de tijd. Als dit zo is, moet het dominerende model van ons universum, ΛCDM, aangepast worden. De huidige resultaten, waarbij \(w\) zelfs onder de -1 komt, zijn zeker nog controversieël, aangezien dit een van de belangrijkste aannames in de natuurkunde breekt. Dit onfysische gedrag zou echter nog goed kunnen verdwijnen als nauwkeurigere metingen beschikbaar komen, of een net iets ander model dan \(w_0 w_a\)CDM wordt aangenomen.
Bij de huidige resultaten zijn gegevens van 14 miljoen sterrenstelsels en quasars verzameld. DESI gaat nog tot 2026 door met data verzamelen, en verwacht wordt dat daarmee de 14 miljoen wordt uitgebreid tot wel 35 miljoen. Vele natuurkundigen en kosmologen zullen vol interesse uitkijken naar de volgende resultaten van deze samenwerking, om te zien of die resultaten de grens van 5 sigma zullen bereiken, of dat toch blijkt dat ΛCDM een goede omschrijving van ons universum is. Theoretisch natuurkundigen – en zeker ook snaartheoreten – zullen erg benieuwd zijn of in nieuwere resultaten nog steeds blijkt dat \(w\) onder de natuurkundige grens van -1 duikt, of dat dit probleem toch wordt opgelost bij betere resultaten. Zoals Pim al schreef in zijn artikel: als definitief wordt vastgesteld dat de kosmologische constante niet constant is, zou dit een van de grootste kosmologische ontdekkingen van deze eeuw zijn. Stay tuned!