Een ladingdichtheidsgolf is een enigszins misleidend woord omdat het suggereert dat zich op bepaalde plekken meer lading bevindt dan op andere, dat wil zeggen: op de ene plek (de piek van de golf) zou de ladingdichtheid hoog zijn en op de andere plek (het dal van de golf) laag. In werkelijkheid is echter niet de ladingdichtheid hoog, maar de elektronendichtheid. Een hoge elektronendichtheid komt echter niet noodzakelijk overeen met een hoge (negatieve) ladingsdichtheid: elektronen (met lading -e) en protonen (met lading +e) trekken elkaar namelijk aan, dus waar veel elektronen zijn, zullen waarschijnlijk ook veel positief geladen atoomkernen zijn. En als elektronen en atoomkernen dicht bij elkaar zitten (ca. \( 70 \cdot 10^{-12} \) m voor een koolstofatoom) ten opzichte van de afstand tussen de atomen (ca. \( 246 \cdot 10^{-12} \) m voor grafiet, dat volledig uit koolstofatomen bestaat), is de ladingsdichtheid in een netto ongeladen materiaal overal praktisch nul.
Als ik in het vervolg over een hoge ladingdichtheid spreek, zal ik de aanwezigheid van veel elektronen bedoelen. Ladingdichtheidsgolven worden gemeten door middel van een ingenieuze ‘elektronenmicroscoop’ die de Scanning Tunneling Microscope (STM) wordt genoemd.2 Een ladingdichtheidsgolf is dan dus aanwezig in een materiaal als er met een STM op bepaalde plekken een hogere elektronendichtheid wordt gemeten dan op andere.3 Als we nu even nadenken over de opbouw van een vaste stof, die bestaat uit gerangschikte atoomkernen met daaromheen een elektronenwolk, dan heeft zo’n materiaal een ladingdichtheidsgolf. Op plekken waar een atoomkern zit, bevinden zich namelijk veel elektronen, en tussen de atoomkernen bevinden zich weinig elektronen. De golflengte van zo’n golf komt dan overeen met de afstand tussen de atomen. Je ziet dit weergegeven in afbeelding 1.
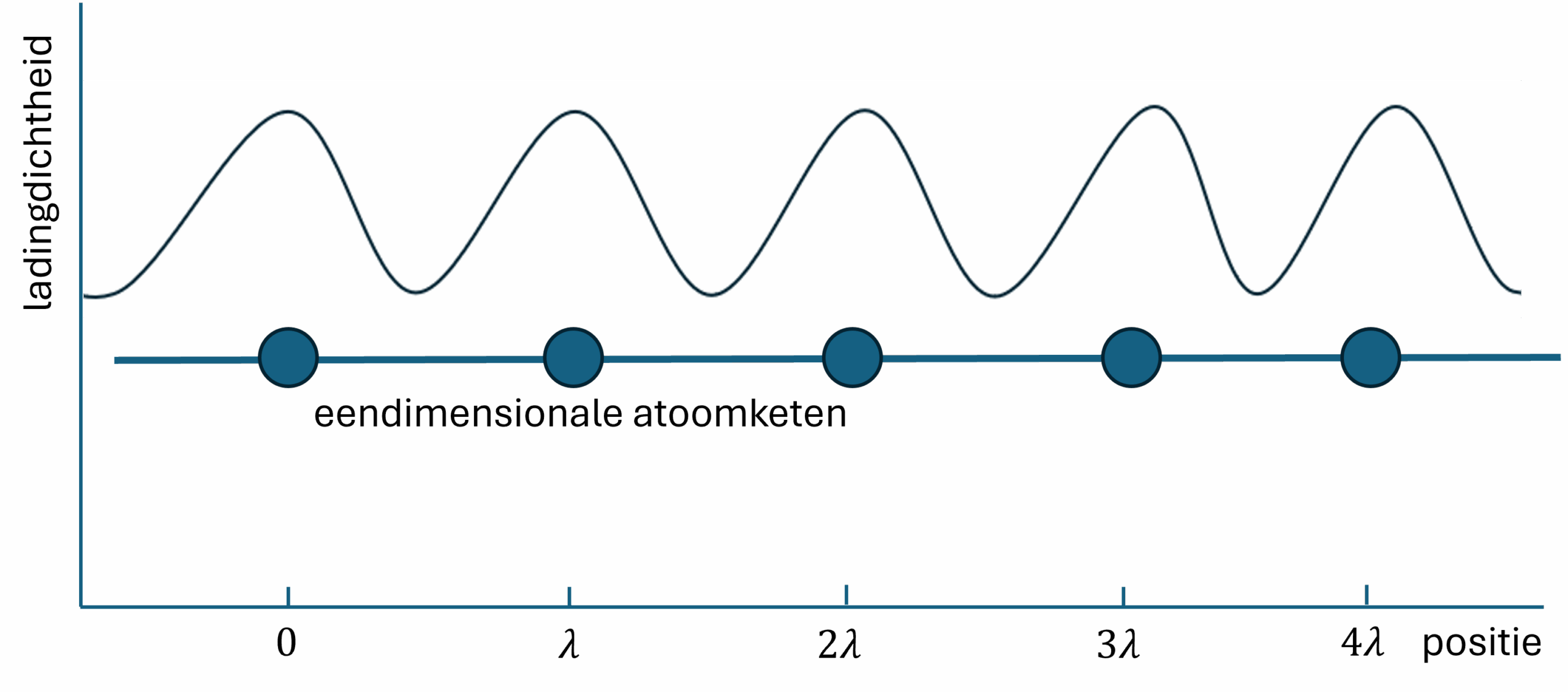
Ladingdichtheidsgolven worden bijzonderder als de golven een golflengte hebben die anders is dan de afstand tussen atomen. De natuurkundige Rudolf Peierls heeft in 1954 een model opgesteld dat uitlegt hoe zulke golven ontstaan in materialen die bestaan uit één eendimensionale atoomketen, zoals in afbeelding 2, waar de ladingdichtheidsgolf een golflengte van twee keer de atoomafstand heeft. Peierls liet zien dat een ladingdichtheidsgolf met een golflengte van twee keer de atoomafstand energetisch voordelig is wanneer de atomen in paren naar elkaar toe bewegen, zoals ook weergegeven in afbeelding 2. De elektronen zitten dan het liefst tussen twee dicht bij elkaar liggende atomen, omdat ze hier dicht bij twee atoomkernen zijn.
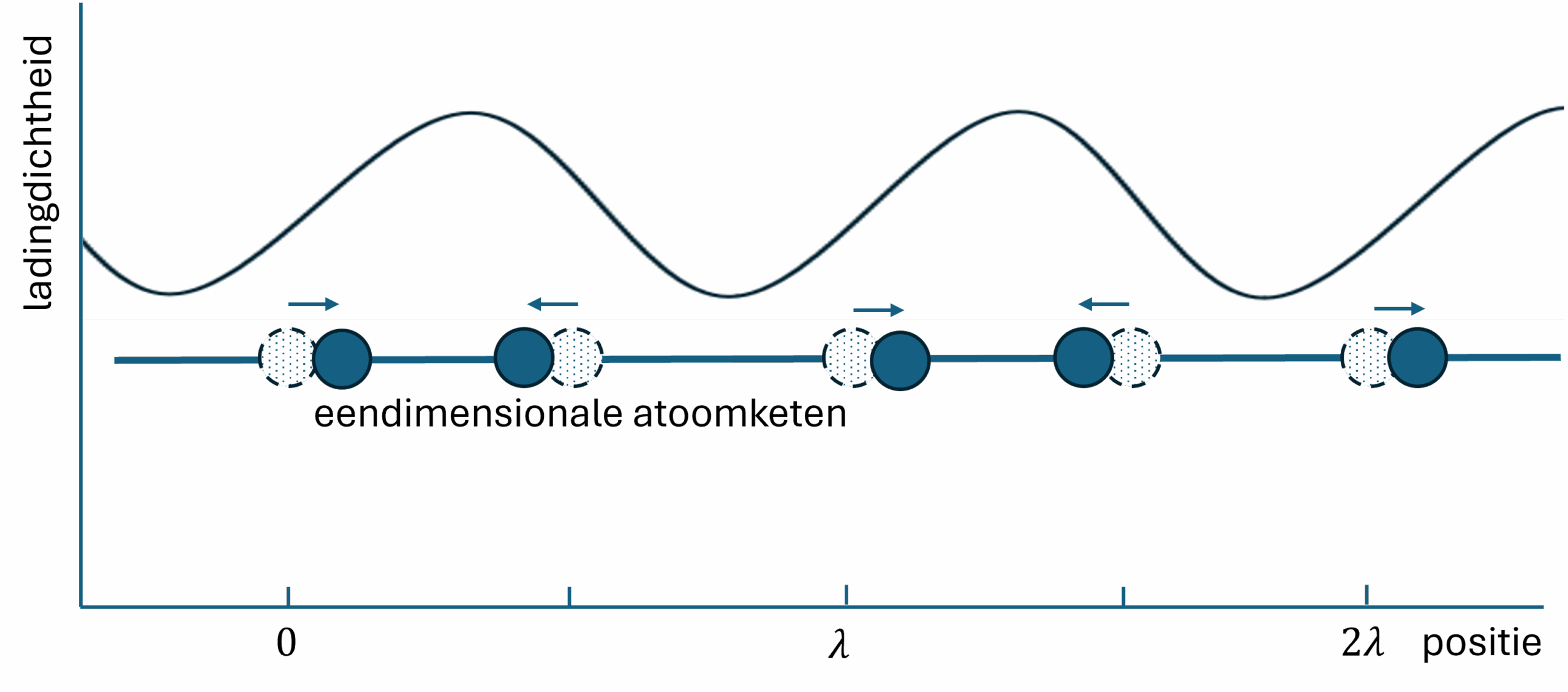
Sinds het eendimensionale model van Peierls is er steeds meer theoretisch begrip gekomen over het ontstaan van ladingdichtheidsgolven en zijn deze golven in allerlei materialen geobserveerd. Ladingdichtheidsgolven komen vooral voor in zogeheten quasi-tweedimensionale materialen. Deze materialen, waarvan TaS2 een voorbeeld is, bestaan uit ver uit elkaar liggende, opeengestapelde laagjes van steeds dezelfde atoomstructuur. In afbeelding 3 wordt dit weergegeven voor TaS2. Een enkel laagje is drie atomen hoog, en daarmee rond de nanometer (\( 10^{-9} \) m) dik. Het materiaal wordt daarom quasi-tweedimensionaal genoemd. Pas als het materiaal uit ver uit elkaar liggende lagen van slechts één atoom dik bestaat, wordt het materiaal tweedimensionaal genoemd.4 Dit is bijvoorbeeld het geval voor grafiek, waarvan je potlood gemaakt is. Omdat de laagjes koolstof waaruit grafiek bestaat ver uit elkaar liggen, interageren ze zwak. Hierdoor kan je met heel weinig kracht een laagje van het materiaal afhalen. Dit laagje blijft achter op het papier wanneer je schrijft of tekent.
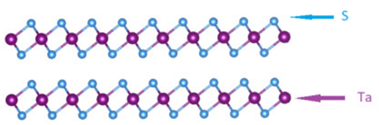
We zijn nu bijna klaar om de mooie ladingdichtheidsgolven in TaS2 te beschrijven en hebben alleen nog wat informatie over de specifieke structuur van dit materiaal nodig. De tantalium- en sulfideatomen in TaS2 zijn gerangschikt zoals in afbeelding 3, dat een zijaanzicht van twee quasi-tweedimensionale lagen weergeeft. Als je van bovenaf op een quasi-tweedimensionale laag kijkt, ziet het atoomrooster eruit zoals in afbeelding 4, waar de paarse stippen nog steeds de tantaliumatomen aangeven en de blauwe stippen de sulfideatomen.

In TaS2 vormt zich niet één ladingdichtheidsgolf, maar drie tegelijk. Dit gebeurt doordat de twaalf tantaliumatomen rondom een centraal tantaliumatoom, naar dit centrale atoom toe bewegen, zoals ik met pijltjes aangeef in afbeelding 5.
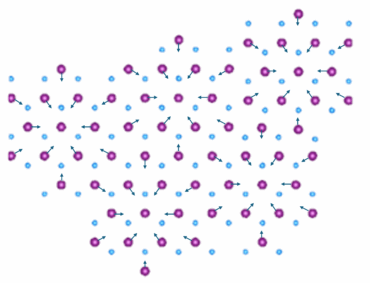
Door deze verplaatsing vormen zich zespuntige sterren van dichter bij elkaar liggende tantaliumatomen, zoals weergegeven in afbeelding 6.
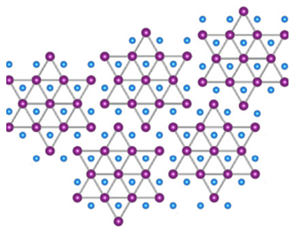
Net als in de eendimensionale atoomketen van afbeelding 2, willen de elektronen daar zitten waar veel atomen zijn. In dit geval komt dat overeen met de middens van de sterren. Ik laat de resulterende ladingdichtheidsgolf samen met de sterren zien in afbeelding 7.
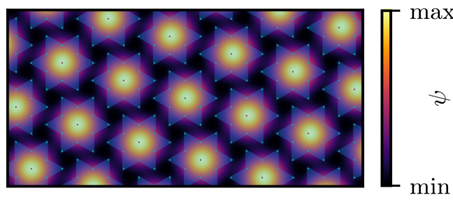
De stervorming en ladingdichtheidsgolf zoals in afbeelding 7 zijn geobserveerd in meerdere materialen en hebben intussen een theoretische verklaring gekregen door middel van de zogeheten Ginzburg-Landautheorie.5 Een ladingdichtheidsgolf zoals in afbeelding 7, die op zich al bijzonder is, komt in TaS2 voor bij relatief lage temperaturen, onder de 180 kelvin – bijna 100 graden onder het vriespunt. TaS2 heeft echter nog twee andere soorten ladingdichtheidsgolven, die voorkomen bij hogere temperaturen.
Boven de 350 kelvin – zo’n tachtig graden celsius – heeft TaS2 een vergelijkbare ladingdichtheidsgolf, maar van een net iets andere golflengte en net iets andere richting dan de golf in afbeelding 7. In het bijzonder is de golflengte niet proportioneel aan een roostervector, waarmee ik een pijl bedoel die van het ene atoom naar het andere atoom wijst. Deze ladingdichtheidsgolf wordt onevenredig genoemd (in het Engels: incommensurate), in tegenstelling tot de evenredige (commensurate) ladingdichtheidsgolf van afbeelding 7. Je ziet de golf in afbeelding 8.

Tussen de 180 en 350 kelvin heeft TaS2 nog een andere soort ladingdichtheidsgolf, die bijna evenredig (in het Engels: nearly-commensurate) genoemd wordt. De bijna-evenredige ladingdichtheidsgolf bestaat uit domeinen van evenredige ladingdichtheidsgolven, met tussen deze domeinen een sterk niet-evenredig deel, zoals weergegeven in afbeelding 9, waar de niet-paarse sterren het gebied tussen de domeinen weergeven.
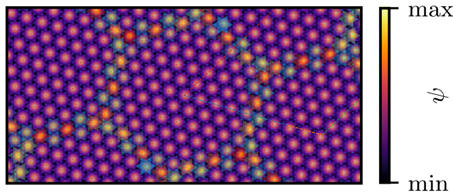
Wanneer je de locaties van de maxima van de ladingdichtheidsgolven tussen twee verschillende domeinen bekijkt, bijvoorbeeld door de rood gestreepte lijn te volgen, zie je dat deze locatie verschuift: in het middelste domein bevinden de maxima zich op de lijn, terwijl in het domein rechtsboven de maxima zich rechts onder de lijn bevinden. En in het domein rechtsonder bevinden de maxima zich links onder de gestreepte lijn. Het blijkt dat de maxima van de ladingdichtheidsgolf met de klok mee roteren ten opzichte van het middelste domein. Vanuit een ander domein kun je precies dezelfde conclusie trekken. Blijkbaar wil de ladingdichtheidsgolf graag draaien tussen de domeinen door. Maar waarom? Welk mechanisme zet deze draaiing in gang? En welke materiaaleigenschap maakt deze draaiende ladingdichtheidsgolf energetisch voordelig? We weten de antwoorden op deze vragen nog niet, maar in mijn huidige onderzoek probeer ik ze te beantwoorden door middel van een veralgemenisering van de eerdergenoemde Ginzburg-Landautheorie. Dus wat maakt TaS2 zo speciaal…? Wordt vervolgd!
[1] Deze resultaten zijn gepresenteerd in het volgende artikel: Singh, Manoj, et al. “Lattice-driven chiral charge density wave state in 1T-TaS2.” Physical Review B 106.8 (2022): L081407.
[2] Hoe deze microscoop precies werkt, leg ik niet uit in dit artikel, maar zie voor meer informatie bijvoorbeeld Wikipedia – Scanning Tunneling Microscope.
[3] Merk op: een ladingdichtheids- of elektronendichtheidsgolf is een quantumeigenschap van een material en de golf duidt op het over de ruimte uitgespreid zijn van de elektronen. Dit is mogelijk vanwege de golf-deeltjesdualiteit.
[4] Merk op dat als we wiskundig precies zijn eigenlijk niets tweedimensionaal kan worden genoemd, omdat iets pas exact tweedimensionaal is als het dikte nul heeft. Iets met dikte nul bestaat echter niet! Om deze reden wordt een materiaal tweedimensionaal genoemd als het de minimale dikte heeft, oftewel: uit een laag van één atoom dik bestaat.
[5] Zie voor meer informatie over deze theorie ook het artikel Classificatie van Fasen op deze website.