Space, time and gravity do not exist on a microscopic scale. New insights in theoretical physics would appear to lead to this surprising conclusion. On a macroscopic scale, these everyday phenomena arise from microscopic physics as ‘emergent’ effects. Last week, physicist Erik Verlinde presented his new theory of emergent gravity, an adaptation of the current gravitational laws of Newton and Einstein. His theory explains both the accelerated expansion of the universe – caused by dark energy – and the extra gravity that is observed at the edge of galaxies, which is commonly attributed to the mysterious ‘dark matter’.
By Manus Visser and Marcel Vonk

Figure 1. Erik Verlinde.In his article ‘Emergent Gravity and the Dark Universe’, which was published last week, the UvA researcher presented his latest insights into the behaviour of gravity.
- Three mysteries about gravity
- A solution: emergent gravity
- Gravity from information
- Entropy and surface area
- Positively and negatively curved space
- Dark energy: a volume contribution to entropy
- The creation of ordinary matter
- A formula for dark matter
- Conclusion
Three mysteries about gravity
Gravity is what keeps our feet on the ground. It makes the earth roughly spherical and makes our planet orbit around the sun. Without gravity, our world would look completely different. And yet, of the four fundamental forces of nature, it is gravity that physicists understand the least.
There are no fewer than three problems associated with our understanding of gravity. Firstly, we do not fully understand how gravity behaves on a microscopic scale. Combining quantum mechanics with the general theory of relativity results in notorious infinities, which would suggest that we cannot simply apply Einstein’s laws at a subatomic level. This conflict is known as the quantum gravity problem.
The second problem originates in cosmological observation. In 1998, two independent teams of astronomers came to the conclusion that our universe is experiencing accelerated expansion. This discovery came as a great surprise to many physicists. After all, gravity is a force that attracts, which should actually slow down the expansion of the universe! To be able to explain the phenomenon of repulsion, it had to be assumed that the universe contains an enormous amount of additional energy. Such energy, also known as dark energy, can be seen as the energy of the vacuum itself. The mysterious dark energy constitutes no less than sixty-nine per cent of the total amount of energy in the universe.
The third problem posed by gravity was identified in the early 1930s by Jan Oort and Frits Zwicky, and was revived in the 1960s and 1970s as a result of observations made by Vera Rubin and Kent Ford. These astronomers discovered that the speed at which stars at the edge of galaxies rotate around the centre is much greater than might be expected in these galaxies on the basis of the visible matter. A similar pattern exists for the speeds at which galaxies rotate around the centre of a cluster of such systems. According to Newton’s theory of gravity, the speed at which distant objects rotate around a large mass concentration reduces as the distance to the centre increases. Astronomers observed, however, that the rotation speeds in the outer regions of many galaxies and clusters actually remain the same or even increase! And despite these high speeds, such stars and galaxies do not deviate from their orbit. Apparently, they are being pulled harder than might be expected on the basis of the visible mass. So where does this additional attracting force come from?
Most researchers attribute this additional gravity to dark matter – matter consisting of particles that remain unknown. And here, too, the effect is enormous: the universe should contain about five times as much dark matter as ordinary, visible matter. Moreover, twenty-six per cent of the content of the universe remains unknown, which, to say the least, is an unsatisfactory situation. Extensive research is therefore currently being carried out to detect the particles, either directly or indirectly, that could make up dark matter.
Erik Verlinde’s new theory, however, predicts that such particles will not be found through these experiments. He believes that the additional attracting force in the outer regions of galaxies has a completely different origin.
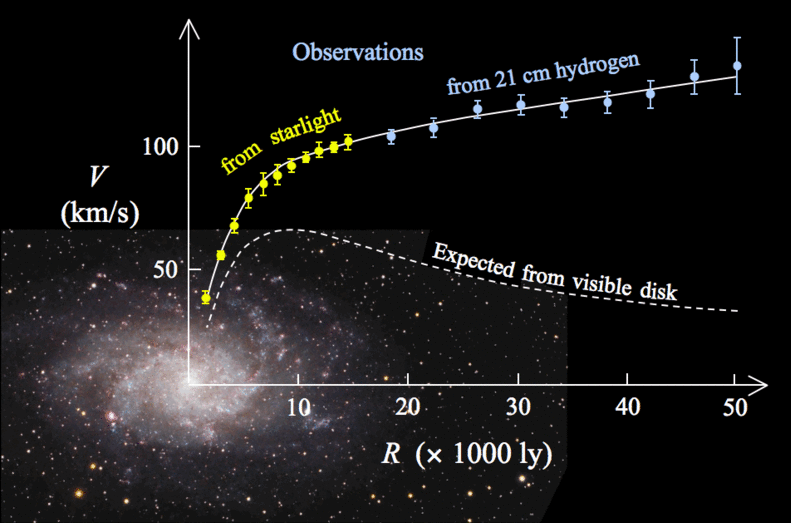
Figure 2. Rotational speed of stars in a galaxyAccording to Newton’s laws of gravity, stars in the outer regions of galaxies should move more slowly the further they are from the core. (Dotted line.) In practice, however, the speed is observed to remain the same or, as in this case, even to increase. (Solid line.) Image: Stefania Deluca.
A solution: emergent gravity
How should we tackle the problems of quantum gravity, dark matter and dark energy? Seeing that all these issues concern the nature of gravity, it is conceivable that they are ultimately interrelated. We might have to change our views about gravity itself in order to throw light on the whole range of problems. And this is precisely what Erik Verlinde hopes to achieve with his new theory.
Verlinde’s ideas build on developments in the physics of black holes and string theory. Back in the 1970s, Stephen Hawking, Jacob Bekenstein and others discovered that the physics of black holes could be described surprisingly well through natural laws derived from thermodynamics. As a result, physicists soon came to the conclusion that gravity – at least near black holes – is a thermodynamic phenomenon.
Thermodynamics deals with macroscopic phenomena, such as heat and pressure, which originate from microscopic physics. Consider the temperature of a cup of coffee, which is produced by the movements of countless individual molecules. Thermodynamic properties such as temperature and pressure do not exist on a microscopic level, but are emergent and are only visible on a macroscopic scale. The relationship between thermodynamics and gravity suggests that gravity – as well as space and time – does not exist on a microscopic scale and only emerges on a larger scale.
This idea of gravity as an emergent force offers an elegant solution to the problem of quantum gravity. After all, gravity does not exist on a quantum level, so there is no need to go looking for laws that unify the theories of relativity and quantum physics! Verlinde’s new insight is that emergent gravity can also solve the other two issues concerning dark energy and dark matter. To understand how that works, we have to go back to what theoretical physicists discovered about the origin of gravity, following Bekenstein and Hawking.
Gravity from information
What are the ‘atoms’ of space-time? In a cup of coffee, the vibrations of the smallest building blocks – atoms and molecules – ensure that the coffee is hot. To understand gravity as a thermodynamic effect, we need to search for the building blocks of the space around us. Many physicists have been occupied with this very question in recent decades.
An important lesson from this research is that ultimately it does not really matter what the atoms of the space-time actually look like. Compare this with the cup of coffee again: in order to understand the thermodynamic properties of coffee, we do not need to know the type of molecules in the coffee or how the atoms in these molecules are actually arranged. Much more important is understanding the total number of molecules or the freedom of movement that these molecules have. In other words: we are interested in the information that the molecules carry with them. And the situation is the same for gravity: in a sense, we can see the information itself as the fundamental building block.
In quantum physics, however, information behaves differently to our expectations. In classical physics, a single unit of information is always located in one particular location. The ‘computer bits’ of classical physics are the properties of individual particles, which are situated at well-defined locations. In quantum mechanics, however, information can also be shared by different particles – a phenomenon that is known as entanglement. Information may, for example, be hidden in a particle pair, with one half located here on earth and the other half on the moon. Quantum information is not localised!
In recent years, vast numbers of theoretical physicists have thrown themselves into trying to understand the consequences of this entanglement. The picture that emerged is that space and time at the quantum level consist completely of – and in a sense even originate from – non-localised information. How can we understand this rather science-fiction-like concept?
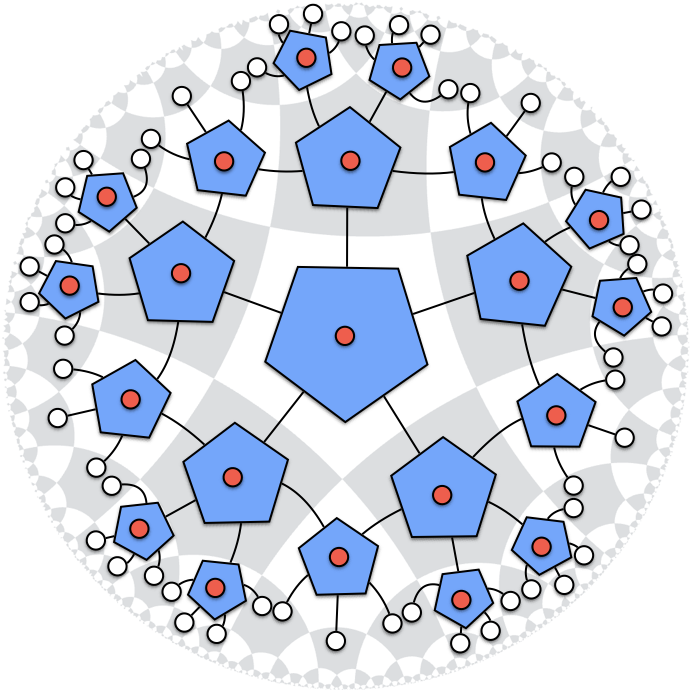
Figure 3. Entanglement and information.To depict the distribution of information throughout space and how that information is entangled, physicists make use of so-called ‘tensor networks’. The figure above is a simple example of such a network. Each circle represents a quantum bit and the lines show the entanglement between the various bits. Image courtesy of ‘Holographic quantum error-correcting codes’ by F. Pastawski, B. Yoshida, D. Harlow and J. Preskill.
Entropy and surface area
Imagine space that at quantum level is broken up into numerous tiny ‘bits’, which are all entangled with each other. On this scale, geometric concepts such as length and surface area mean very little. How does space appear on a macroscopic scale?
In 2010, the Canadian physicist Mark van Raamsdonk had an important insight on this subject. His hypothesis is that space is connected, exactly because bits are entangled at quantum level. We experience space as a continuous whole: you can walk or hover through space without ever encountering areas where ‘there is no space’. Van Raamsdonk’s premise is that the entanglement is the glue that holds together the quantum building blocks of space. It is this glue that ultimately ensures that empty space is connected on a macroscopic scale.
Van Raamsdonk’s hypothesis can also be described in a more quantitative way. His premise is based on a simple formula, taken from the work of Bekenstein and Hawking on black holes, which in the context of quantum information was elaborated on by the Japanese physicists Shinsei Ryu and Tadashi Takayanagi. The formula states the following: if we divide a piece of space into two areas, the amount of entanglement between these areas is equal to
S = A / (4 G ħ)
In this formula, S stands for so-called entanglement entropy – a quantity measuring the amount of information that the two areas share with each other. A is the size of the imaginary surface area that separates the two areas. G and ħ are two natural constants: Newton’s constant, G, determines the strength of gravity, while Planck’s constant, ħ, indicates the scale at which quantum effects play a role.
We can easily understand the structure of this formula. The two areas – let us call them 1 and 2 for the sake of convenience – share non-localised quantum information, because there are quantum bits in area 1 that are entangled with quantum bits in area 2. If we view entanglement from the perspective of Van Raamsdonk’s hypothesis as the property that connects space, it is clear that most of the entanglement takes place around the boundary between 1 and 2. The amount of information that the two areas share, S, is therefore proportional to the surface area of that boundary, A. The factor 4Għ determines the precise relationship between the two variables.
This phenomenon, that an amount of information is related to a surface area, proves to be an essential feature of Einstein’s theory of gravity. In 1995, Ted Jacobson demonstrated that this relationship is actually necessary for Einstein’s laws of gravity to be deduced. Conversely, a correction to this relationship would therefore inevitably lead to a modification of the laws of gravity. Where might such a correction come from?
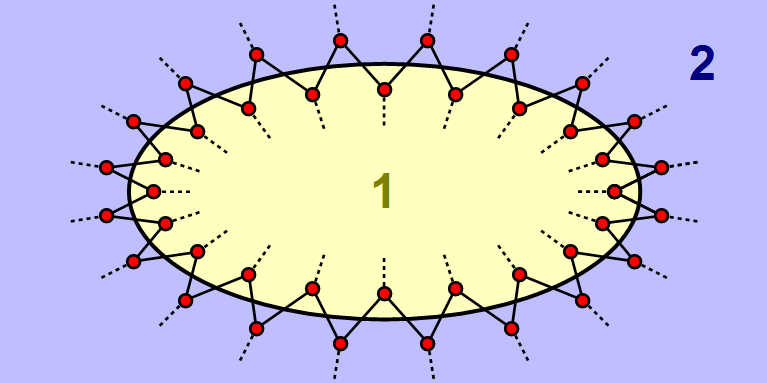
Figure 4. Entanglement, information and surface area.If entanglement connects space, the entanglement between bits in area 1 and bits in area 2 will primarily occur around the surface area that separates the areas. It is not surprising, therefore, that the information the areas share is also proportional to the size of that surface area.
Positively and negatively curved space
The geometric properties of space around us greatly influence the nature of gravity. On a large scale, our universe is not a flat stage: space is curved. According to theory, such curvature can take two forms. The universe can be ‘positively’ curved, like the surface of a sphere, or ‘negatively’ curved, like a horse’s saddle. There is a direct connection between this curvature and the mystery of the repulsion of dark energy. A negative curvature of the universe should lead to a major additional attracting force. In our universe, however, the opposite scenario is taking place: dark energy produces a positive curvature, which in turn is causing the repulsive force that is observed in the accelerating expansion of space.

Figure 5. Positive and negative curvature.On the left is a positively curved surface area, and on the right a surface area with negative curvature. Our four-dimensional space-time can be positively and negatively curved in a similar way.
In order to demonstrate the relationship between information and surface area, Ryu and Takayanagi had to assume that space is negatively curved. However, as already indicated, we do not live in a negatively curved universe, but in positively curved space, also known as De Sitter space. On a large scale, where the curvature of the universe plays a role, the theoretically better understood negatively curved scenario – which unsurprisingly is called Anti-de Sitter space – is only an approximation of reality.
The major difference between Anti-De Sitter space and De Sitter space is that the latter contains energy. Anti-De Sitter space can be seen as an ‘empty’ vacuum state, whereas De Sitter space is a highly energetic state. The additional energy in De Sitter space is the dark energy that causes the expansion of the universe.
The questions that Verlinde asked himself are: what impact do the additional energy and additional curvature have on the distribution of information in space-time and what effect does this have on gravity? He soon realised that the formula of Ryu and Takayanagi, which relates information and surface area, needed to be analysed in more detail.
Dark energy: a volume contribution to entropy
Does the relationship between information and surface area also apply in De Sitter space? According to Verlinde the answer is ‘yes’, but besides the surface area component there is another contribution to entropy. In Verlinde’s model, this additional information, which is associated with dark energy, is spread throughout space. And for this reason, this contribution depends on the volume of a unit of space and not on its surface area.
This relationship can once again be expressed in a formula. The additional volume contribution to the entropy within a spherical surface area is equal to
S = A R / (4 G L ħ)
L represents the cosmological scale: the distance to the edge of the visible universe. A = 4 π R2 is the surface area of a spherical piece of space with radius R, and G and ħ are Newton’s and Planck’s constants, as before.
In order to understand that this expression actually concerns a contribution that is proportional to the volume, we need to realise that the volume of a sphere is represented by V = 4/3 π R3. Using some simple algebra, the formula above can be written as
S = V / V0
in which V0 stands for the combination 4 G ħ L / 3. We can think of V0 as the volume that one bit of information in the dark energy occupies: according to the formula, the total volume divided by V0 is equal to the amount of information in the dark energy, S. It is important to note that the volume contribution (2) to the entropy will usually be much smaller than the surface area contribution (1). The two expressions differ from each other by a factor R / L. If we take R to be the radius of our Milky Way galaxy, for example, this factor is roughly equal to 0.00001.
The next question is therefore: if the volume contribution to the entropy is so small, even on a galactic scale, can it still have a discernible effect? Surprisingly enough, Verlinde’s theory answers this question affirmatively. The volume contribution ensures that it is precisely on the scale of galaxies that the laws of gravity of Newton and Einstein no longer exactly apply.

Figure 6. Information in De Stitter space.Because De Sitter space is filled with dark energy, not all information can be contained at the boundary. It is precisely the information in the dark energy itself, here shown schematically by the blue squares, which is proportional to the volume.
The creation of ordinary matter
Of course, the universe does not consist of dark energy alone. It also contains the ordinary matter from which everything we see around us is made. Only when we add ordinary matter to de Sitter space does it become clear that existing laws of gravity need to be adjusted.
According to Verlinde, ordinary matter can be created by removing dark energy from the universe and localising it somewhere. However, the creation of such a mass, like the sun, leaves a permanent ‘scar’ in De Sitter space. The universe remembers, as it were, that a mass has been created. Firstly, this causes space to curve, and causes other masses, like the earth, to be drawn to the matter. Einstein described this curvature in his general theory of relativity.
There is, however, a secondary effect. The creation of a mass also affects the distribution of information present in the dark energy. Some of the information is now associated with the matter, while the remaining information must rearrange itself in space. Mass, therefore, relocates information. Action, however, always leads to reaction: the information also ‘pushes’ back. On the scale of galaxies and galactic clusters, so much energy is removed that this effect, irrespective of the relatively small contribution of the dark energy to the total information, is still significant. The resulting additional force is therefore observed on this scale: it is exactly the force that is attributed to the dark matter!
Again, this statement can be made quantitative. Empty space is created in areas where information is removed, while the space outside is still filled with information and energy. The majority of empty space is therefore found around matter. This means that at a certain distance around a mass there is a transition from empty space to filled space.
Verlinde calculates this transition distance as follows. In his model of emergent gravity, the amount of information that is associated with matter and which is removed from the dark energy is equal to
SM = 2 π M R / ħ
SM is the amount of ‘removed’ information, M is the mass of the matter and R is the radius of the volume in which this matter is located. The transition from empty space to filled space occurs exactly when the amount of information that is associated with the dark energy (equation (2)) begins to dominate over the amount of information removed by the matter (equation (3)). The gravitational effects that are attributed to dark matter will therefore start to occur when
A / (4 G ħ) > 2 π M L / ħ
This formula is written in such a way that the familiar combination from the formula of Ryu and Takayanagi (formula (1)) is on the left. The surface area A that can be calculated from this formula indicates the boundary of the volume beyond which ‘dark matter’ in a galaxy, for example, will play a role. The size of this boundary turns out to be consistent with what is actually observed in galaxies.
Note that in the formula above the cosmological scale L occurs. This factor originates from the earlier formula (2), for the amount of information present in dark energy. Surprisingly, the additional gravity that we observe on the scale of individual galaxies is therefore determined by physics on the scale of the whole universe!

Figure 7. Matter in De Sitter space.Matter, such as a galaxy, is formed from the information associated with the dark energy. This creates an area of ‘empty’ space, which at a certain distance becomes space filled with information. Around galaxies, this distance corresponds with the observed distance at which ‘dark matter’ starts to play a role.
A formula for dark matter
The above explanation serves as motivation for Verlinde for deriving his most important result: a general relationship between the actual amount of normal matter and the apparent amount of dark matter. As already indicated, according to Verlinde, this dark matter does not exist, but we are able to describe its attributed effects on the basis of an effective mass – the mass which the dark matter would have had if it had been the explanation for the additional gravity. Verlinde deduces the following relationship for this effective mass, MD:
2 π L / ħ (MD)2 = MB / 3 A / (4 G ħ)
Here, MB is the amount of ordinary (‘baryonic’) matter; all other symbols are as described above. Two things are striking about this formula. Firstly, it once again contains the cosmological scale L: again we see that the size of the effect of dark matter is determined by physics on the scale of the whole universe. And secondly, it is noteworthy that a connection between the amount of ordinary matter and the apparent amount of dark matter exists at all. This is a manifestation of what is explained above: ‘dark matter’ is a reaction force that occurs when information is removed in order to form ordinary matter. It is therefore not surprising that there is a connection between the two. Verlinde’s formula demonstrates this connection very accurately.
Conclusion
Emergence, the creation of gravity on a large scale from the distribution of information on a small scale, addresses three problems at the same time. Firstly, gravity as we know it does not exist on a microscopic scale and therefore an understanding of the laws of gravity on a quantum scale is unnecessary. Secondly, space on a quantum scale consists of information bits that are entangled with each other. If the microscopic state of all bits has a high energy, space seen on a large scale is De Sitter space. This explains the origin of dark energy. Thirdly, the creation of a mass in De Sitter space relocates the information associated with the dark energy. This relocation of information has implications for masses that are located, for example, at the edge of a galaxy. This reaction force corresponds to the effects that are attributed to the mysterious dark matter.
Solving three problems in one go is a wonderful prospect, but can Verlinde’s ideas be put to the test? They certainly can: we have seen that his theory not only offers qualitative descriptions, but also provides quantitative formulas that can be verified through observational data. Conversely, falsification is, of course, also possible: as soon as one of the many current quests results in finding an actual matter particle to provide an explanation for the dark matter, Verlinde’s theory will obviously be incorrect.
But even if Verlinde’s theory is correct, there is still much work to be done. One major open question, for example, is how the dynamics of the universe enters into his formulation: can this theory also offer an accurate description of the history of the universe and the movement of matter and ‘dark matter’ over the course of time? Can it be used to explain the properties of cosmic background radiation, the light coming from the early universe that we are still observing today? In addition, in some observations, such as those of the so-called Bullet Cluster, not only the relationship between ordinary and ‘dark’ matter is measured, but also the way in which these two appear to be distributed over space. This distribution does not always prove to be nicely symmetrical, and it therefore offers a wonderful challenge for Verlinde’s model to explain such observations.
Whatever the case may be, Erik Verlinde’s ideas do sound appealing and offer an interesting alternative view to decades-old fundamental problems concerning gravity. Hopefully, within the not too distant future, his theory will contribute to gaining a clear understanding of the everyday force that we have been experiencing for millions of years.
Translation: UvA Talen.