In het eerste deel van deze serie over fouriertransformaties en fourieranalyses kwamen we enkele real-lifetoepassingen van moderne wiskundige technieken tegen, en zagen we de oorsprong van deze technieken in de context van de warmtevergelijking. Het bleek dat fouriertransformaties een grotere rol spelen dan op het eerste gezicht lijkt: de quantummechanica barst van de fouriertransformaties, zoals met name volgt uit het feit dat plaats en snelheid ‘elkaars fouriergetransformeerde’ zijn. Naast fouriertransformaties heb ik ook fourieranalyses geïntroduceerd. Voor de duidelijkheid: een fourieranalyse vertelt je hoe je een fouriertransformatie kunt doen. In andere woorden: de analyse vertelt je welke ‘golven’ je met welk relatief gewicht moet optellen om van een functie de fouriergetransformeerde te vinden. Op dit laatste ga ik in dit artikel wat dieper in, want fourieranalyses blijken zeer sterk gerelateerd aan het vinden van tijdsafhankelijke quantummechanische golfuncties door een methode die ‘Fourier’s truc’ genoemd wordt.
De schrödingervergelijking oplossen
De schrödingervergelijking oplossen. Dat is feitelijk wat een groot deel van de natuurkundigen tracht te doen, dag in, dag uit. In wiskundige termen is deze vergelijking te omschrijven als een lineaire, partiële differentiaalvergelijking. Dat is een hele mond vol, maar het betekent twee op zich begrijpelijke dingen. Dat de vergelijking ‘lineair’ is, betekent dat je oplossingen van deze vergelijkingen kunt optellen en vermenigvuldigen met een constante, en zo weer nieuwe oplossingen vindt. Dat deze vergelijking daarnaast een ‘partiële differentiaalvergelijking’ is, betekent dat er verschillende componenten in voorkomen die afhankelijk zijn van verschillende variabelen, zoals bijvoorbeeld de plaats en de tijd.
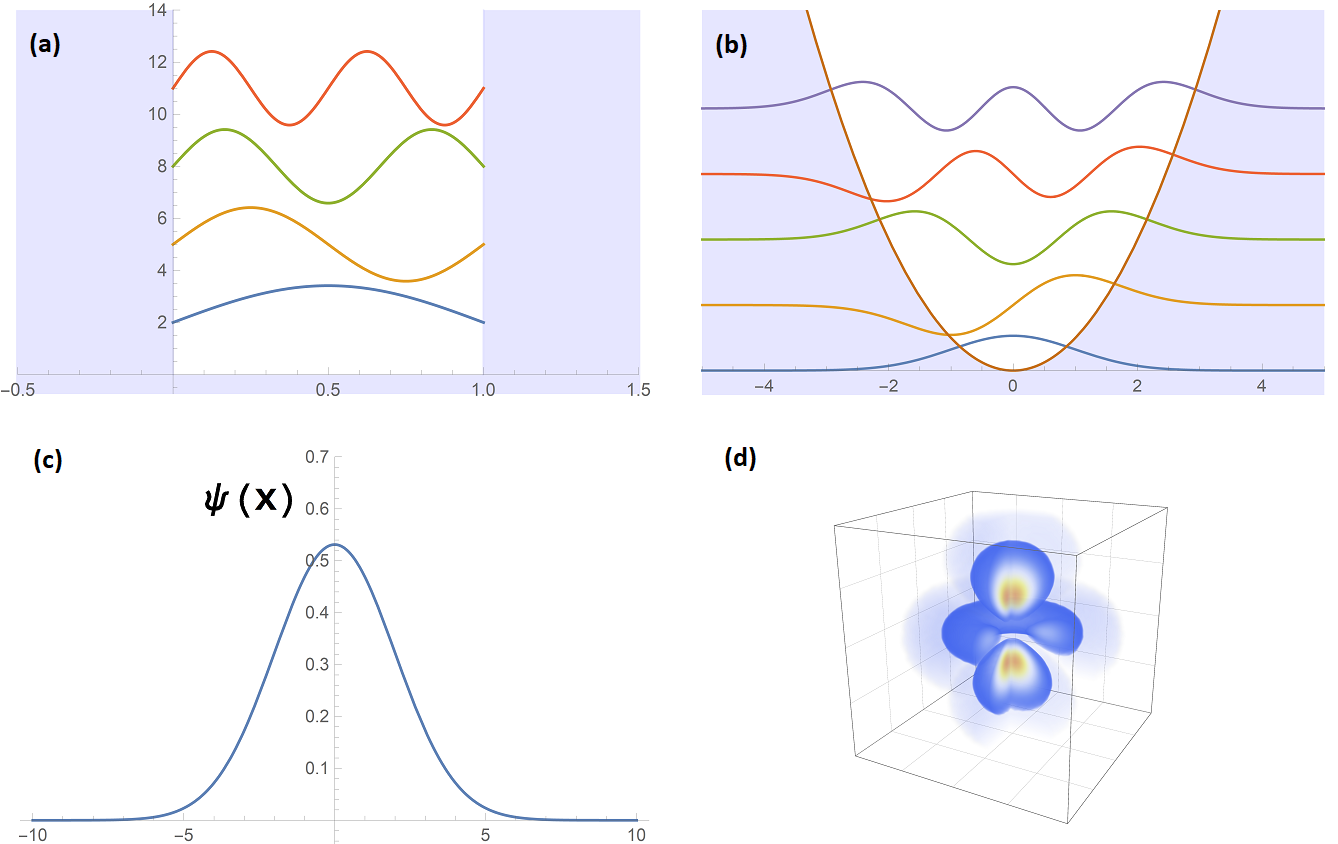
De schrödingervergelijking oplossen is bijzonder complex! Er zijn dan ook zeer weinig natuurkundige systemen te bedenken waarvoor we de vergelijking daadwerkelijk exact kunnen oplossen. De meeste inleidende boeken voor quantummechanica hebben het slechts over 4 á 5 systemen (zie afbeelding 1). Deze verschillende systemen zijn herkenbaar aan hun potentiaal: een potentiaal bepaalt hoe moeilijk het is – hoeveel potentiële energie het kost – voor een deeltje om op een bepaalde plaats te zijn. Voor het gemak heb ik in een deel van de afbeeldingen ook de potentiaal ingekleurd. Alleen al over deze ‘makkelijke’ systemen zou ik enkele hoofdstukken kunnen schrijven, maar dat zal ik hier niet doen. Wij gaan namelijk kijken naar de oplossingen van deze systemen.
De schrödingervergelijking is op deze website al heel vaak genoemd en beschreven. Waar ik de lezer dit keer op zou willen wijzen, is iets wat waarschijnlijk niet eerder genoemd is: de gelijkenis tussen de schrödingervergelijking en de warmtevergelijking (zie afbeelding 2). Hopelijk valt het op dat de vorm van de twee vergelijkingen grofweg dezelfde is: de vergelijkingen zijn allebei voorbeelden van lineaire, partiële differentiaalvergelijkingen!
\(\frac{\partial u(x,t)}{\partial t} = K \frac{\partial^2 u(x,t)}{\partial x^2} \\\),
\(-i\hbar \frac{d}{dt} \Psi = \hat{H} \Psi, \qquad \mbox{met} \; \hat{H} = -i \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V(x)\).
Afbeelding 2. De warmte- en de schrödingervergelijking. De warmtevergelijking (boven) is al uitgebreid ter sprake gekomen in het eerste deel van deze serie. Het valt op dat deze vergelijking erg lijkt op de onderste vergelijking, de schrödingervergelijking. Er zijn echter ook een paar grote verschillen tussen deze twee vergelijkingen: de schrödingervergelijking is een vergelijking voor complexe functies, wat blijkt uit de factor ‘i’, en de vergelijking bevat de quantummechanische constante ħ, die de constante van Planck wordt genoemd. De H-term heet de ‘Hamiltoniaan’ van het systeem en bestaat uit een dubbele afgeleide naar de plaats, een term die geassocieerd is met kinetische energie, en een term V(x), die de potentiaal beschrijft. Voorbeelden van verschillende potentialen zijn te zien in afbeelding 1.
Zoals bekend uit het eerste deel van deze serie, kan fourieranalyse gebruikt worden om de exacte, tijdsafhankelijke oplossing van de warmtevergelijking te vinden van een metalen staaf die afkoelt in een koude omgeving. (Zie afbeelding 5 in het eerste deel van de serie.) Het oplossen van de schrödingervergelijking is helaas iets ingewikkelder dan het oplossen van de warmtevergelijking, omdat in het geval van de schrödingervergelijking vrijwel alle termen operatoren zijn: ingewikkelde voorschriften die van een functie een andere functie maken. Zulke operatoren gedragen zich niet zo netjes als (vermenigvuldiging met) gewone getallen, en moeten op een speciale manier behandeld worden.
Desondanks is het mogelijk om de schrödingervergelijking op te lossen (soms zelfs exact, zoals bij de systemen die zijn weergegeven in afbeelding 1, en anders in een willekeurig goede benadering), en de technieken die gebruikt worden om de oplossingen te vinden zijn precies zoals bij de warmtevergelijking. Merk op dat hierbij ook de tijdsafhankelijkheid van de oplossing wordt bepaald: de linker term in de schrödingervergelijking (de afgeleide naar de tijd) vertelt je hoe de oplossing in de loop van de tijd verandert.
Alle systemen in afbeelding 1 vallen opvallend genoeg binnen dezelfde klasse van quantumsystemen, namelijk die systemen waar de potentiaal onafhankelijk is van de tijd! Dit is op zich geen raar fenomeen. Een alledaags voorbeeld van een potentiaalbarrière die we allemaal wel eens moeten overwinnen is dat van een brug. De brug blijft als het goed is altijd staan, en verandert niet van vorm in de loop van de tijd, wat betekent dat de potentiaalbarrière onafhankelijk van de tijd is. Let op: dat de barrière niet afhangt van de tijd, wil nog niet zeggen dat de oplossing van de schrödingervergelijking niet van de tijd afhangt – net zoals de plek waarop jij je op je fiets bevindt wel degelijk verandert in de loop van de tijd!
In het geval van tijdsonafhankelijke potentialen is het mogelijk om voor de schrödingervergelijking een wiskundige oplosmethode te gebruiken die bekend staat als ‘scheiding van variabelen’. Men splitst daarbij de differentiaalvergelijking in verschillende stukken die ieder onafhankelijk van elkaar op te lossen zijn. De oplossing voor het totaal is dan simpelweg het product van de oplossingen van de individuele vergelijkingen. Het is op dit punt dat onze goeie oude fourieranalyses de kop op steken: die spelen een belangrijke rol als het gaat om het vinden van de tijdsafhankelijkheid van de golffuncties die we willen beschrijven.
Laat ik de laatste zinnen van de bovenstaande alinea iets concreter maken. De schrödingervergelijking lossen we, zoals gezegd, op door middel van het scheiden van variabelen. Dit betekent dat we de linkerkant van de schrödingervergelijking en de rechterkant ervan apart van elkaar kunnen oplossen. De exacte wiskunde hierachter is niet heel ingewikkeld, maar omwille van leesbaarheid zal ik die hier niet in detail beschrijven. Het resultaat is dat we twee verschillende golfvergelijkingen krijgen: één voor de tijdsafhankelijkheid van de golffunctie (de linkerkant van afbeelding 2b), en één voor het tijdsonafhankelijke deel (de rechterkant van die afbeelding). Deze ‘rechterkant’ ziet er altijd uit als \(-\hbar^2/2m d^2/dx^2\), de ‘kinetische energie van een deeltje’ en een term \(V(x)\) die de potentiaal beschrijft, en die in ons geval alleen afhangt van de plaats ‘x’, maar niet van de tijd.
Deze methode van het scheiden van variabelen wordt zo vaak gebruikt, dat deze tweede vergelijking (die met alleen het kinetische en potentiele deel) een aparte naam heeft: de tijdsonafhankelijke schrödingervergelijking. Laten we nu even ervan uitgaan dat het lukt om deze vergelijking op te lossen. Dat is best lastig, maar, zoals eerder in dit stuk aangegeven is er in elk geval één fysisch systeem wat we exact kunnen oplossen: het waterstofatoom. Voor allerlei andere systemen kunnen we op zijn minst een benaderde oplossing maken. De ‘rechterkant’ oplossen zal er nu toe leiden dat we een set basisoplossingen, de zogeheten eigenfuncties \(\psi_n\) krijgen (dit zijn bijvoorbeeld de verschillende golfjes die getekend zijn in afbeelding 1a en 1b). De eigenfuncties zijn functies die ieder onafhankelijk een oplossing zijn van de ‘rechterkant’, en die een prachtige eigenschap hebben: indien men de functie invult in de tijdsonafhankelijke schrödingervergelijking, dan vinden we exact dezelfde functie terug, maar vermenigvuldigd met een eigenwaarde \(E_n\). Deze waarde identificeren we met de energie van deze specifieke eigenfunctie.
Samenvattend zien de oplossingen van de ‘rechterkant’ van de schrödingervergelijking er dus als volgt uit:
\(\hat{H} \psi_n = E_n \psi_n\)
Afbeelding 3. De tijdsonafhankelijke schrödingervergelijking en zijn oplossingen. De Hamiltoniaan H is ook te zien in het rechterlid van de schrödingervergelijking in afbeelding 2. Als je de bovenstaande vergelijking oplost, krijg je een hele serie oplossingen ψn, genaamd eigenfuncties. Elk van deze oplossingen is een legitieme oplossing van de tijdsonafhankelijke vergelijking. Omdat de vergelijking lineair is, is de meest algemene oplossing een optelsom van deze individuele oplossingen. Een voorbeeld van de individuele eigenfuncties zijn de golven die getekend zijn in afbeelding 1a en 1b. De getallen En zijn de eigenwaardes die horen bij de eigenfuncties ψn. Elke ψn heeft zijn eigen bijbehorende eigenwaarde. De eigenwaardes zijn in dit geval getallen die de energie aangeven die hoort bij de toestand die de eigenfunctie ψn beschrijft.
De ‘n’ is hier niets anders dan een label om bij te houden over welke oplossing we het hebben. Als we niet geïnteresseerd waren in tijdsafhankelijkheid, zouden we hier stoppen: we hebben de quantummechanische tijdsonafhankelijke golffuncties gevonden als een som van alle mogelijke \(\psi_n\)’s! Maar: natuurlijk zijn we wél in de tijdsafhankelijkheid geïnteresseerd.
Nu zijn we bijna zover dat fourieranalyse een rol zal gaan spelen, maar laten we eerst de volledige oplossing van de tijdsafhankelijke schrödingervergelijking opschrijven. Het resultaat is betrekkelijk eenvoudig (dat wil zeggen: het echt zware werk hebben we met het oplossen van de tijdsonafhankelijke vergelijking al gedaan): de oplossingen zijn de eigenfuncties zoals we die gevonden hadden in afbeelding 3, vermenigvuldigd met complexe e-machten: \(e^{-iE_n t}\). Voor wie niet weet wat een complexe e-macht precies is: het gaat hier om tijdsafhankelijke functies die ‘golven’, net zoals sinus- en cosinusfuncties dat doen. Het is belangrijk om nog eens te vermelden dat \(E_n\) overeenkomt met de energie die hoort bij de specifieke eigenfunctie van \(\hat{H}\). Onthoud dat immers elke eigenfunctie een bijbehorende eigenwaarde heeft. De exacte en meest algemene tijdsafhankelijke oplossing voor de schrödingervergelijking is daarom een som van verschillende tijdsafhankelijke bijdragen, elk met een eigen gewicht \(a_n\):
\(\Psi(x,t) = \sum_n a_n \psi_n(x) e^{-i \hbar E_n t}\).
Afbeelding 4. De exacte oplossing. De exacte tijdsafhankelijke oplossing voor de schrödingervergelijking is een som van termen. Elke term bestaat uit de eigenfunctie ψn zoals ook te zien in afbeelding 3, vermenigvuldigd met een complexe e-macht waar de tijdsafhankelijkheid in zit. Elke term heeft daarnaast ook nog een factor an, die bepaalt hoeveel deze specifieke term bijdraagt aan de totale oplossing. Het vinden van de getallen an gebeurt aan de hand van fourieranalyses, en heet ook wel ‘Fourier’s trick’.
Ik voel me wel genoodzaakt om te herhalen dat dit resultaat alleen nuttig is als men in staat is om in de eerste instantie de eigenfuncties \(\psi_n\) te bepalen uit de tijdsonafhankelijke schrödingervergelijking, iets wat écht een complexe opgave is! Maar ben je eenmaal zover, dan kun je nu fourieranalyse gaan toepassen.
Fourieranalyse en Fourier’s trick
De totale tijdsafhankelijke oplossing is een som van alle tijdsonafhankelijke golffuncties, de \(\psi_n(x)\), die ieder een eigen, aparte, tijdsafhankelijkheid krijgen door middel van de e-macht. De individuele componenten die de het eindantwoord opmaken evolueren dus ieder onafhankelijk van elkaar in de tijd!
Laat ik nu aan de hand van een voorbeeld Fourier’s trick introduceren. We beschouwen voor het gemak een deeltje in een oneindig diepe potentiaalput (afbeelding 1a). Stel dat de golffunctie op tijdstip t = 0 (aangegeven met \(\Psi(x,0)\)) er als volgt uit ziet:
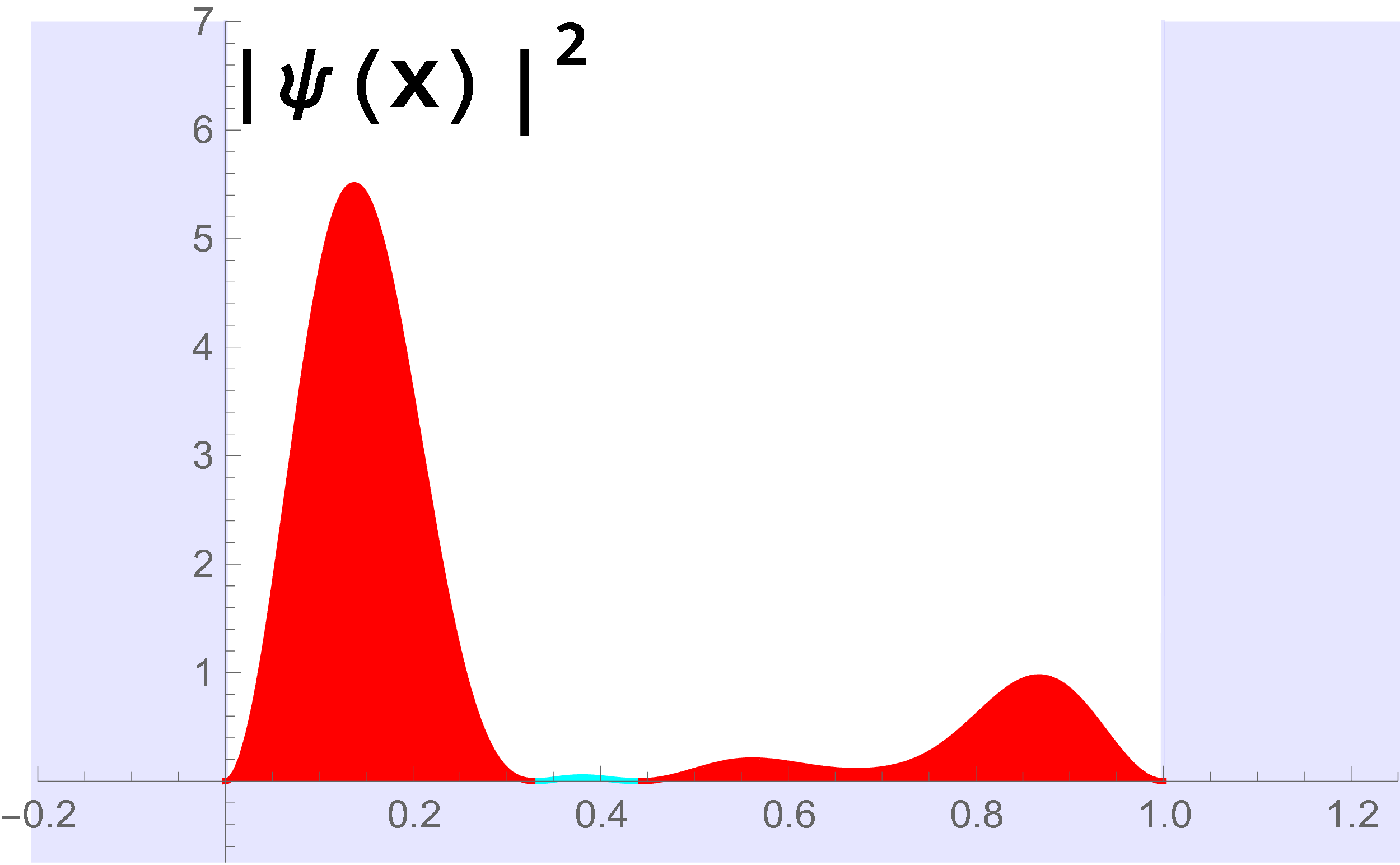
De vraag is nu: hoe zal deze golf, die we nu alleen nog op tijdstip t = 0 hebben getekend, zich in de loop van de tijd gaan gedragen? Om hier achter te komen, zullen we er eerst achter moeten komen uit welke tijdsonafhankelijke golffuncties \(\psi_n\) deze start-golffunctie is opgebouwd. Hier komt de truc: fourieranalyse! Alles wat we hoeven te doen is de bovenstaande golf fourieranalyseren, en we weten welke golven (welke eigenfuncties) een bijdrage leveren aan de golf in afbeelding 5. Het is deze specifieke toepassing van fourieranalyse die een eigen naam heeft gekregen: Fourier’s trick. Eigenlijk is dat best raar, aangezien het niets anders is dan een ‘normale’ fourieranalyse. Hoe dan ook, het blijkt dat de golf hierboven te schrijven is als de volgende som:
\(\Psi(x,0) = 0.72 \sin(\pi x) + 0.29 \sin(2\pi x) + 0.96 \sin(3\pi x) + 0.48 \sin(4\pi x) + 0.55 \sin(5\pi x)\).
Afbeelding 6: Fourierreeks van de golf in afbeelding 5. De sinussen in deze formule zijn de eigenfuncties ψn zoals te zien in afbeelding 3 en 4. De getallen voor deze sinussen zijn de getallen ψn uit afbeelding 4.
Het ‘gewicht’ \(a_1\) is dus bijvoorbeeld 0,72. De energie die hierbij hoort kunnen we ook vinden. Omdat de berekening niet echt belangrijk is voor dit artikel geven we alleen het resultaat: de bijbehorende energie is \(\pi^2 \hbar^2 / 2\). Daarmee kunnen we de eerste term in de som die de volledige tijdsafhankelijke golffunctie beschrijft opschrijven: \(0.72 \sin(\pi x) * e^{-i \hbar (\pi^2 \hbar^2)/2 t}\). (Een opmerking terzijde voor natuurkundig geschoolden die zich verbazen over het feit dat in de e-macht maar liefst drie factoren \(\hbar\) voorkomen: dat komt doordat we in afbeelding 6 wat slordig zijn geweest, en de sinussen als argument een veelvoud van x hebben meegegeven – de eenheden in alle vergelijkingen zijn daardoor niet heel natuurlijk.)
Het bovenstaande proces kunnen we herhalen voor elke term in de fourierexpansie in afbeelding 6, en daarmee we vinden onze tijdsafhankelijke golffunctie. Dat wil zeggen: we kunnen nu op elk tijdstip bepalen hoe de quantumgolf eruit ziet! Het eindresultaat heb ik in het filmpje hieronder weergegeven. De kleuren komen weer overeen met de ‘complexe fase’ van de golffuncties, en zijn verder niet van belang. Een hoge geconcentreerde piek betekent dat het deeltje hoogstwaarschijnlijk daar gevonden zal worden. Zoals je kunt zien zit het deeltje op een rare manier ‘heen en weer te springen’ in de put – we zien hier quantummechaica in actie!
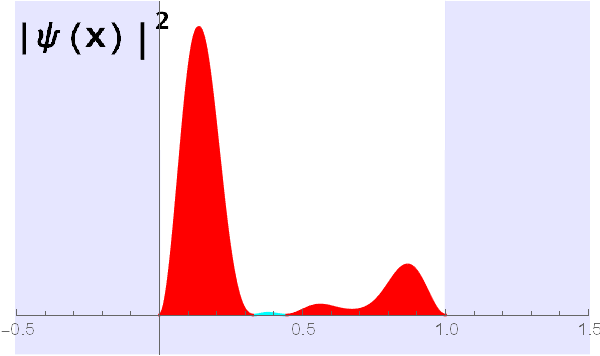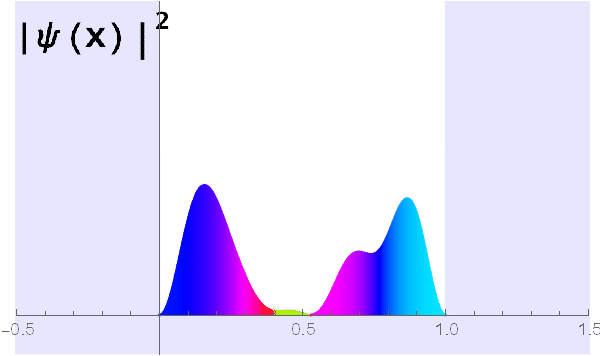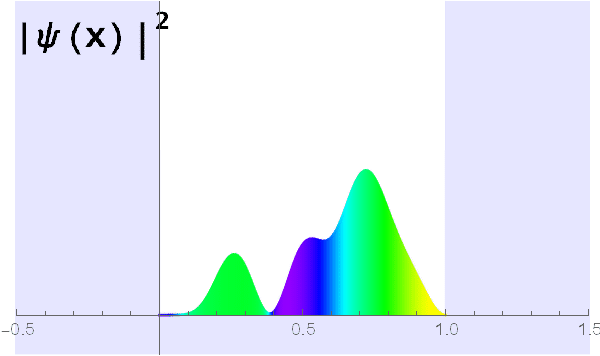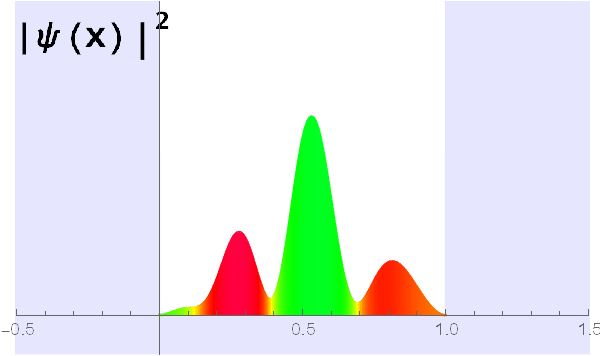
Tijdsafhankelijke golffunctie van het waterstofatoom
Dit proces van het vinden van tijdsafhankelijke golffuncties kunnen we ook doorlopen voor complexere systemen. Ikzelf vind het plaatje rechtsonder in afbeelding 1 erg mooi, dus ik vroeg me af of ik een vergelijkbare tijdsafhankelijke golffunctie voor een waterstof atoom kon maken. Het proces is precies hetzelfde als hierboven voor het deeltje in de put: vind de juiste eigenfuncties van de tijdsonafhankelijke schrödingervergelijking, gebruik Fourier’s trick om erachter te komen welke golffuncties een bijdrage leveren aan de initiële tijdsonafhankelijke golffunctie (in ons geval ‘kies’ ik gewoon een willekeurige begintoestand van het waterstofatoom), en schrijf vervolgens de volledige tijdsafhankelijke golffunctie op!
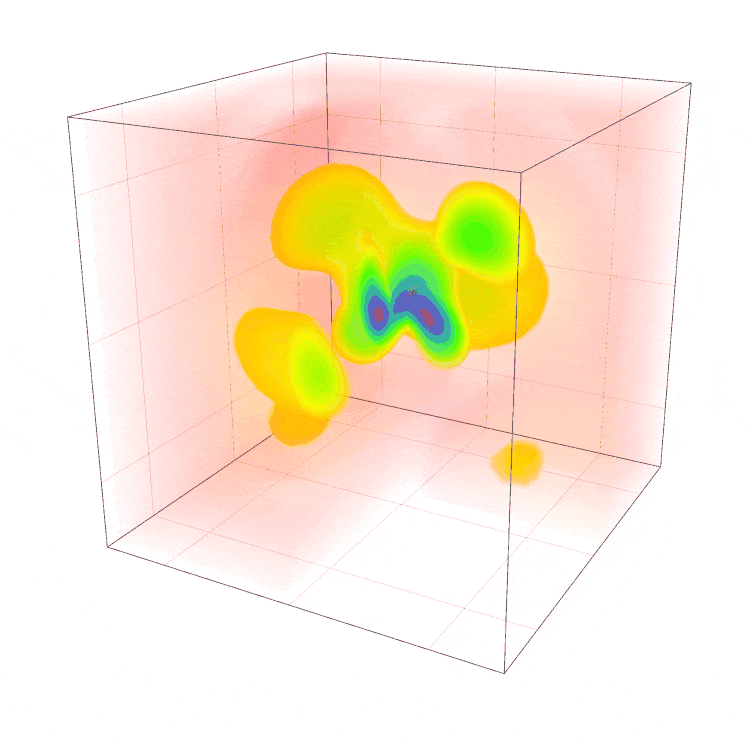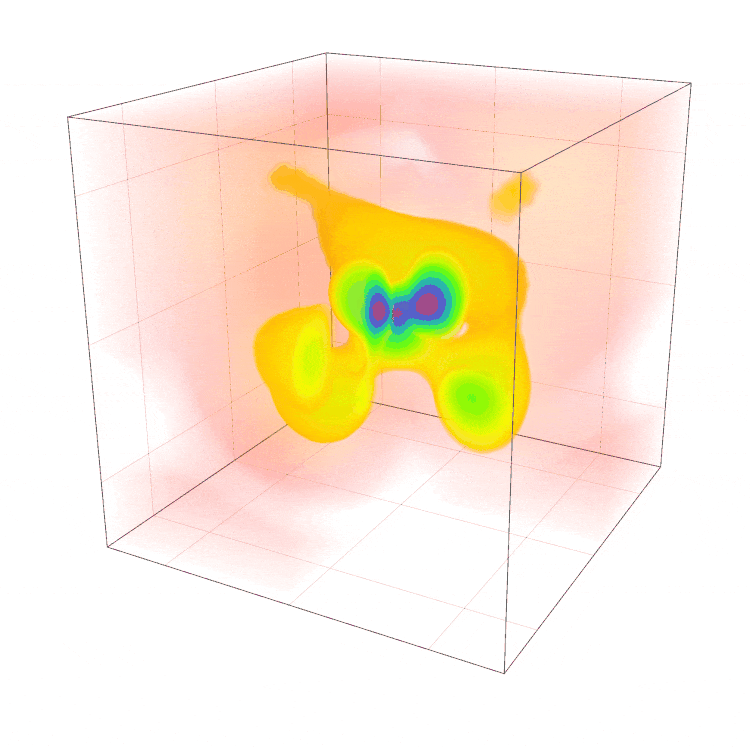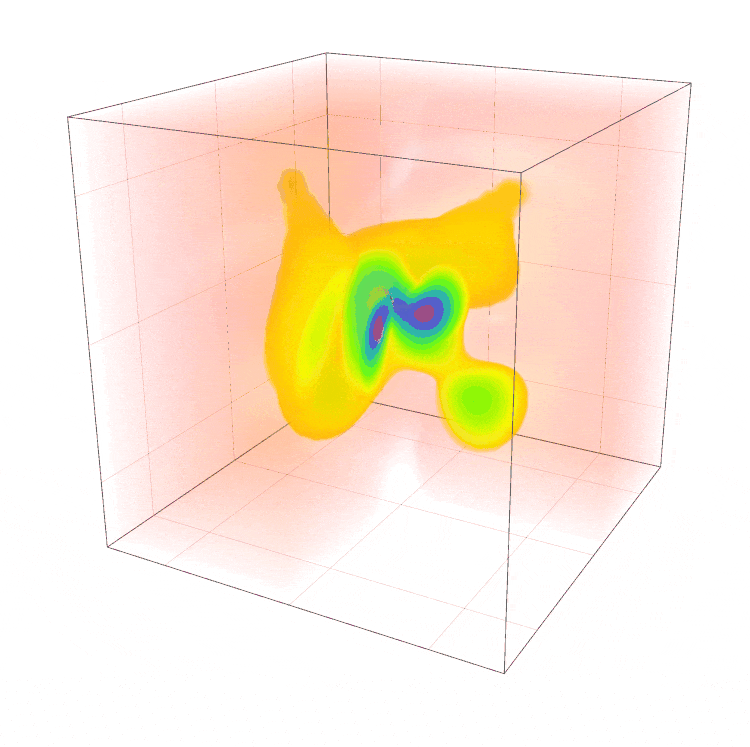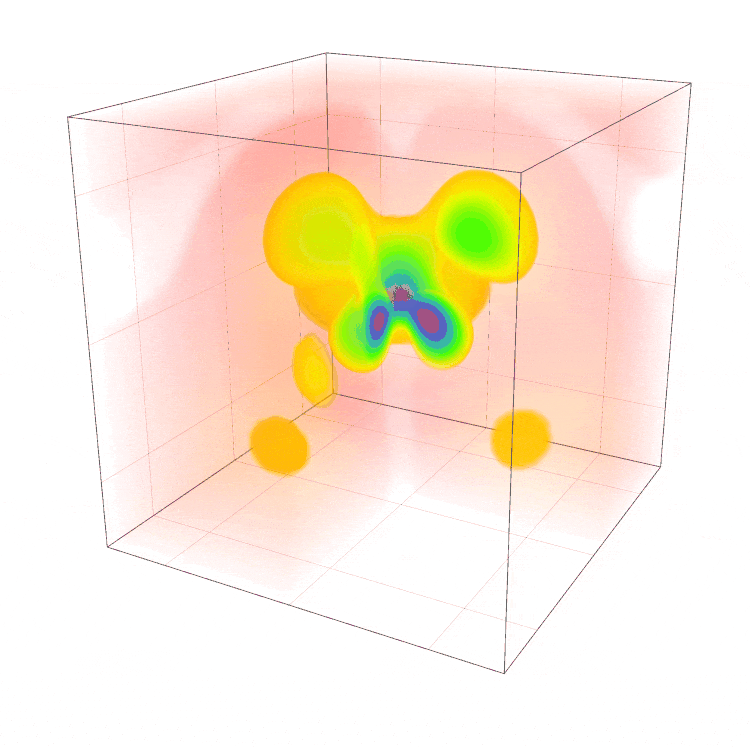
Afbeelding 8: Tijdsafhankelijk filmpje van waterstof. De kleur geeft aan hoe waarschijnlijk het is om een deeltje ergens te vinden. Roder komt overeen met een kleinere waarschijnlijkheid, terwijl blauw overeenkomt met hoge waarschijnlijkheid. In dit gifje van een waterstofatoom heb ikter illustratie een dwarsdoorsnede gemaakt door een hoek van het plaatje ‘eruit te knippen’. Hierdoor kun je de binnenkant zien, en dus ook de plekken waar het elektron zich waarschijnlijker zou bevinden, namelijk ergens binnenin de oranje ‘bubbels’.
Fourieranalyses en -transformaties vinden we zó vaak terug in de natuurkunde, dat het onmogelijk zou zijn om alle toepassingen op deze website te beschrijven. In dit artikel illustreerde ik hoe fourieranalyse gebruikt wordt om de tijdsafhankelijke oplossing voor quantummechanische golffuncties te vinden door middel van Fourier’s trick. Er zijn natuurlijk nog veel meer leuke voorbeelden waar fouriertransformaties een rol spelen, maar die bewaar ik voor latere artikelen in deze serie!