
Het Lenz-Ising-model
Het Ising-model (of Lenz-Ising-model) werd in 1920 door Wilhelm Lenz bedacht, en hij gaf zijn student Ernst Ising de opdracht het uit te werken. In de simpelste variant van het model, en ook de situatie die Ising analytisch wist op te lossen, wordt er een ééndimensionaal rooster beschouwd: een serie punten op gelijke afstanden op een lijn. Het model kan echter ook in meerdere dimensies gedefinieerd worden. Op elk roosterpunt bevindt zich een ‘deeltje’ met waarde +1 of -1. Door verschillende betekenissen aan die waarden te verbinden, kunnen verschillende systemen worden beschreven. In het geval van magnetisme geven we de waarden de betekenis ‘spin omhoog’ of ‘spin omlaag’. Je kunt de ‘spin’ dus zien als de richting van het magneetveld van één enkel deeltje; wil je preciezer weten wat spin is, lees dan bijvoorbeeld dit artikel. Ook bijvoorbeeld legeringen (mengsels van een metaal en een ander materiaal) kunnen worden beschreven aan de hand van het Ising-model. Bij bijvoorbeeld brons, een legering van koper en tin, zouden we +1 kunnen associëren met een koperatoom en -1 met een tinatoom.

Laten we voor nu de magnetisme-interpretatie kiezen, aangezien Ising graag wilde weten of het model bepaalde eigenschappen van magnetisme zou kunnen beschrijven. In de simpelste variant van het model hebben de verschillende spins interacties met alleen hun directe buren. Afhankelijk van de situatie willen naastgelegen spins dezelfde kant op wijzen (zoals bij ferromagnetisme, wat je in veel magnetische materialen waaronder ijzer tegenkomt) of juist andersom uitgelijnd zijn (anti-ferromagnetisme).
Daarnaast kan er ook een extern magnetisch veld worden aangebracht. Dit betekent dat het energetisch voordelig is voor de spins om in dezelfde richting als het magneetveld te wijzen.
Dit alles kan worden samengevat in de hamiltoniaan van het systeem, een grootheid die aangeeft hoeveel energie het het systeem kost om een bepaalde configuratie aan te nemen:
\( H = -\sum_{\text{buren }i,j} J \sigma_i \sigma_j -B \sum_i \sigma_i. \)
De spin van roosterpunt \(i\) wordt aangegeven met \(\sigma_i\). Als \(\sigma_i=+1\), dan wijst de spin omhoog, bij \(\sigma_i=-1\) wijst de spin omlaag. \(J\) beschrijft de koppeling tussen de spins op naast elkaar gelegen roosterpunten. Als \(J\) positief is, dan is de waarde van de hamiltoniaan lager als de spins dezelfde kant op wijzen, terwijl bij een negatieve \(J\) naastgelegen spins juist de tegenovergestelde kant op willen wijzen. De absolute waarde van \(J\) geeft aan hoe sterk de interactie is. Tot slot is er nog het externe magneetveld \(B\). Bij een positieve waarde van \( B \) kost het minder energie als alle spins omhoog wijzen, bij negatieve waarde juist andersom. Ook hier geeft de absolute waarde aan hoe sterk het magneetveld is.
De kans op een bepaalde configuratie \(s\) kan nu worden berekend aan de hand van de volgende formule:
\(P_T(s) = \frac{e^{-H(s)/(k_B T)}}{\sum_{s’} e^{-H(s’)/(k_B T)}}.\)
Hierin is \(T\) de temperatuur en \(k_B\) de Boltzmannconstante – vernoemd naar Ludwig Boltzmann, vorige week nog besproken in dit artikel door Jort de Groot. Als de temperatuur heel laag is, worden configuraties met een hoge energie sterk exponentieel onderdrukt in deze formule. Bij een lage temperatuur zal het systeem zich dus bijna altijd in de grondtoestand – de laagst energetische toestand – bevinden. Bij hogere temperaturen is deze onderdrukking minder sterk en zullen er dus meer thermische fluctuaties plaatsvinden.
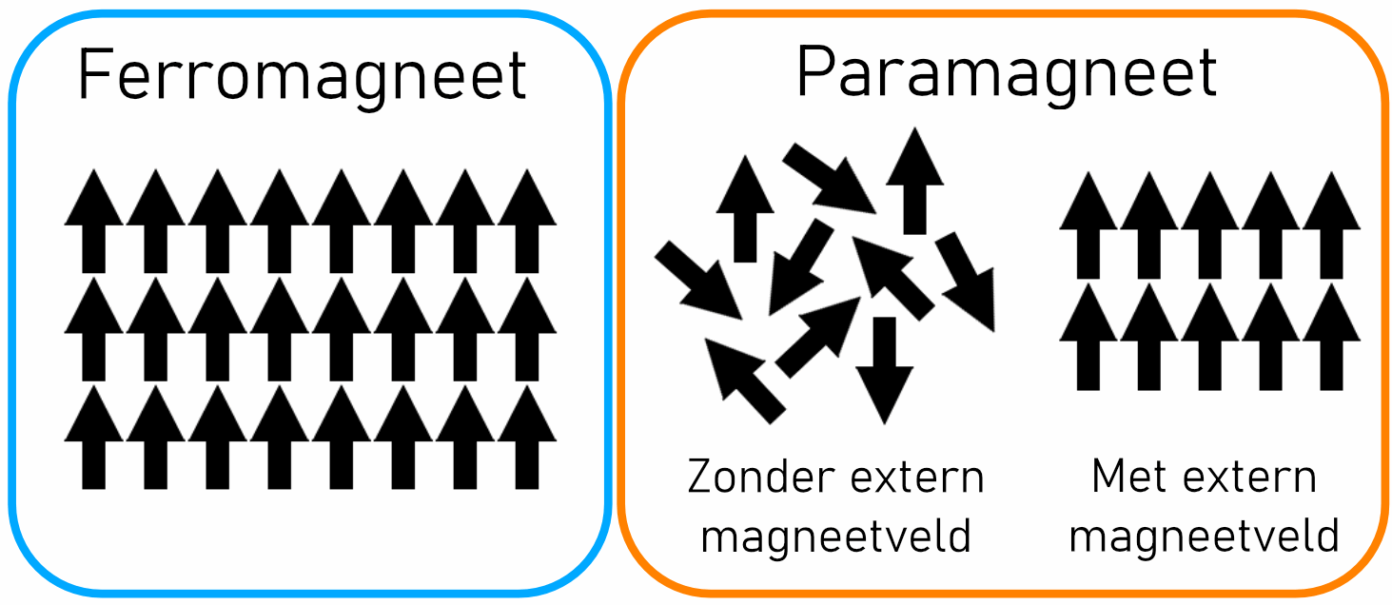
Ferromagneten zijn magneten die alleen onder een bepaalde temperatuur – de Curietemperatuur \(T_c\) – magnetisch zijn. Boven die temperatuur worden het zogeheten paramagneten, die alleen gemagnetiseerd worden in de aanwezigheid van een extern magneetveld. Dit komt doordat bij deze temperatuur de onderdrukking van de toestanden met hogere energie niet meer sterk genoeg is om het systeem te dwingen in de grondtoestand te blijven. Ising was benieuwd of deze eigenschap van ferromagneten te beschrijven viel aan de hand van dit Lenz-Ising-model.
Het lukte hem het ééndimensionale Ising-model op te lossen en hij publiceerde het resultaat, eerst in zijn dissertatie en een jaar later in een kort artikel. Het resultaat was wellicht een beetje teleurstellend: in één dimensie heeft het Ising-model géén faseovergang. Dit betekent dat er niet zo’n Curietemperatuur bestaat waaronder het systeem zich gedraagt als ferromagneet en daarboven als paramagneet: bij alle temperaturen is het een paramagneet. Ising gaf hierdoor de hoop voor dit model op en concludeerde dat waarschijnlijk in hogere dimensies ook geen faseovergang zou plaatsvinden.
Het ontbreken van spontane magnetisatie (ferromagnetisme) kan ook kwalitatief worden begrepen, zonder in details te treden over Isings berekening. Stel je voor dat alle spins dezelfde kant op wijzen: dit komt overeen met complete magnetisatie. Als nu door een thermische fluctuaties er slechts één spin wisselt van richting, is het voor alle spins aan de linker- (of juist rechter-) kant van die ene spin juist voordeliger om ook allemaal om te klappen. Het omdraaien van slechts een enkele spin in één dimensie verbreekt compleet alle communicatie tussen beide helften – de omgeklapte spin is een soort “muur” waar je niet omheen kunt – en hierom is het relatief makkelijk voor het systeem om niet in de grondtoestand te zitten.
Hieruit blijkt ook waarin Ising misschien iets te snel het model van hem en zijn begeleider in de prullenbak gooide: in twee of meer dimensies is er nog wél contact mogelijk met de spins aan de andere kant van de ‘omklapper’ en is het dus lastiger om de magnetisatie teniet te doen.
In 1944 wist Lars Onsager, een Noors-Amerikaanse wetenschapper, ook het tweedimensionale Ising-model analytisch op te lossen en te laten zien dat er daar wel degelijk een faseovergang plaatsvindt! Een leuke manier om zelf met dat model te spelen is bijvoorbeeld deze simulatie, waarbij je de temperatuur en het externe magneetveld kunt aanpassen en kunt zien welk effect dit heeft op de energie en magnetisatie in het systeem.
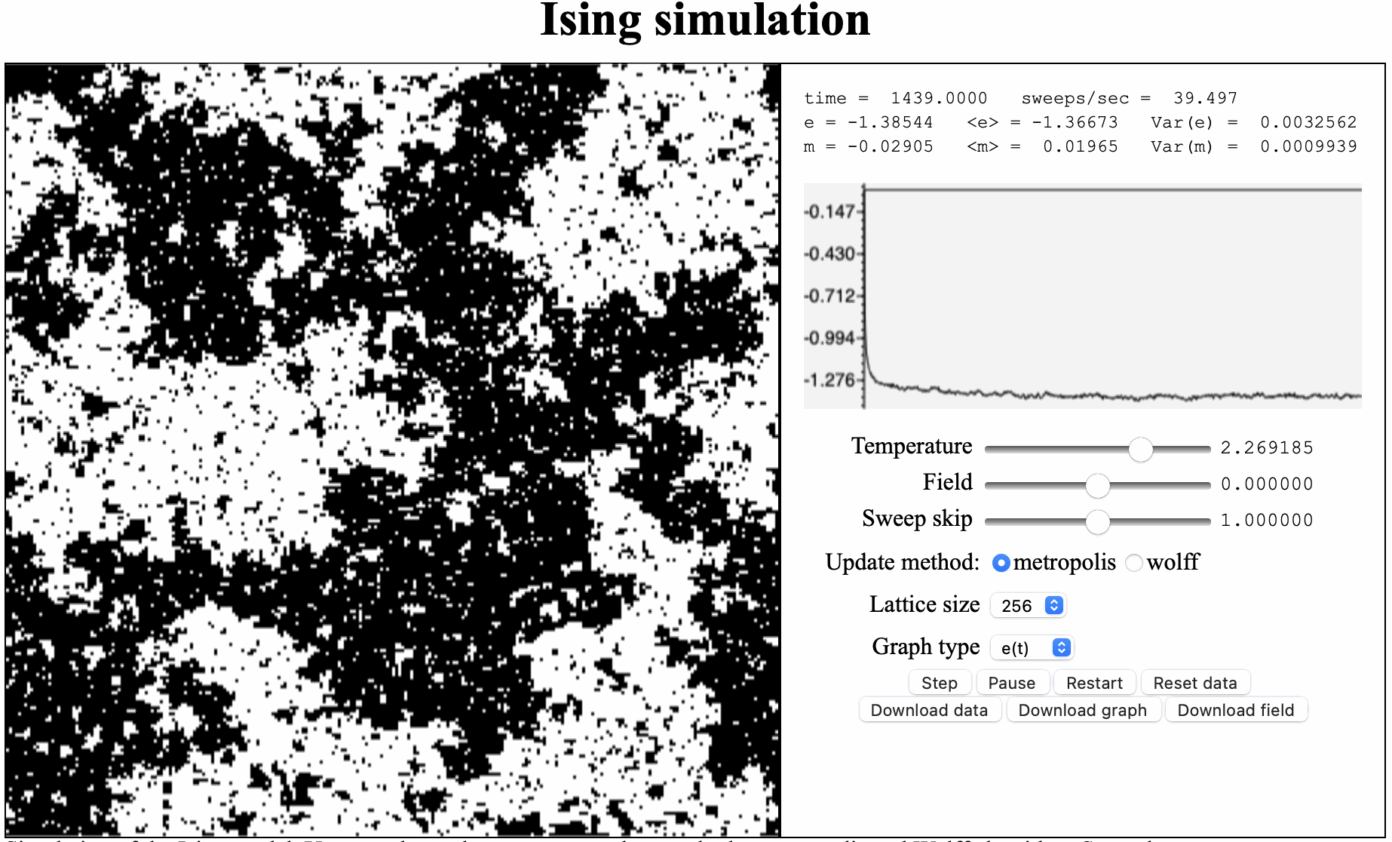
Het feit dat het Ising-model relatief weinig ingrediënten heeft en tóch fysisch interessante fenomenen zoals faseovergangen kan beschrijven maakt het zo speciaal. Door de eenvoud van het model is het niet alleen toe te passen op magnetisme, maar ook op bijvoorbeeld legeringen en zelfs gassen. Het Ising-model beschrijft namelijk niet de natuurkundige krachten die ten grondslag liggen aan de interacties, maar de hamiltoniaan geeft een effectieve en algemene beschrijving van energieconfiguraties die in allerlei verschillende systemen voorkomen. Als een wiskundig model op veel plekken in de natuurkunde voorkomt, noemen we dit een vorm van universaliteit – een eigenschap die wetenschappers graag zien. Een ingewikkeld systeem kan hiermee op relatief eenvoudige wijze beschreven worden.
Ondanks de relatieve eenvoud in één en twee dimensies is het Ising-model in drie dimensies een nog onopgelost probleem. Er bestaan wel veel numerieke resultaten en analytische resultaten in bepaalde grensgevallen (bijvoorbeeld bij heel lage temperaturen), maar 100 jaar na het oorspronkelijke artikel van Ising is er nog altijd geen analytische oplossing voor het driedimensionale Ising-model gevonden.
Het Ising-model is ook een rijk model: er kunnen vele aspecten aan veranderd worden om net andere systemen te beschrijven. Zo kunnen interacties afhankelijk zijn van de precieze roosterpunten, kunnen ook interacties verder dan de directe buren worden meegenomen of kan zelfs de reactie op het externe magneetveld gevarieerd worden per roosterpunt. Deze combinatie van rijkdom en eenvoud maakt dat menig natuurkundestudent de tanden mag zetten in het Ising-model, om door verschillende situaties te simuleren kennis te maken met de fascinerende vakgebieden van statistische fysica en magnetisme.