Hoe complex is de natuur? (2)

Afbeelding 1. Golven.Golfverschijnselen – of het nu gaat om watergolven, geluidsgolven of golven in het elektromagnetische veld – kunnen goed beschreven worden met complexe getallen. Afbeelding: Kai Stachowiak.

Golven

Verrassend genoeg zijn er talloze plaatsen in de natuurkunde waar complexe getallen opduiken. Eén reden daarvoor is dat golfverschijnselen met behulp van complexe getallen vaak veel eenvoudiger te beschrijven zijn dan met reële getallen. Dat heeft vooral te maken met een bijzondere eigenschap van machtsverheffen met complexe getallen. In afbeelding 2 zien we in een animatie het getal

2^it

getekend als een rode stip in het complexe vlak. Hierbij is de waarde van de variabele t geïnterpreteerd als een tijdstip. We zien dat getallen van deze vorm zich op een cirkel bevinden, en dat die cirkel met constante snelheid doorlopen wordt als we t veranderen. Overigens hadden we ook 3^it of 17^it op deze manier kunnen tekenen; het enige verschil zou dan zijn dat de cirkel met een andere snelheid doorlopen wordt.

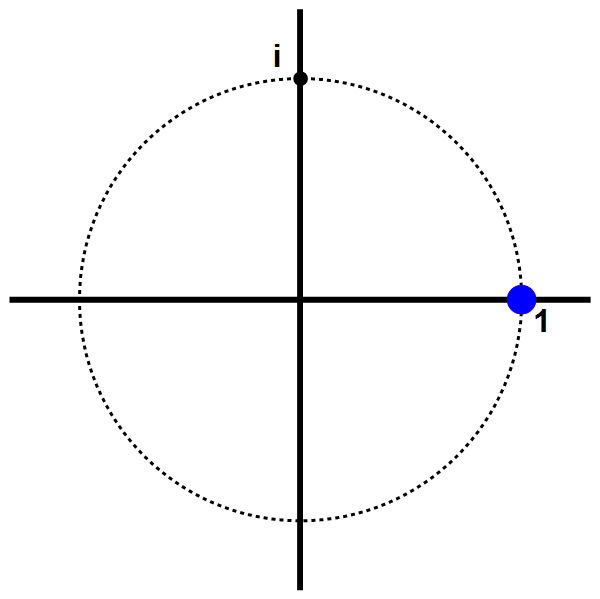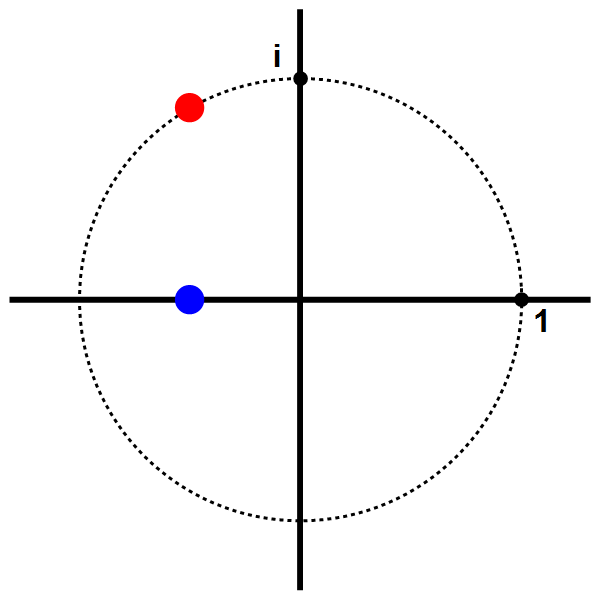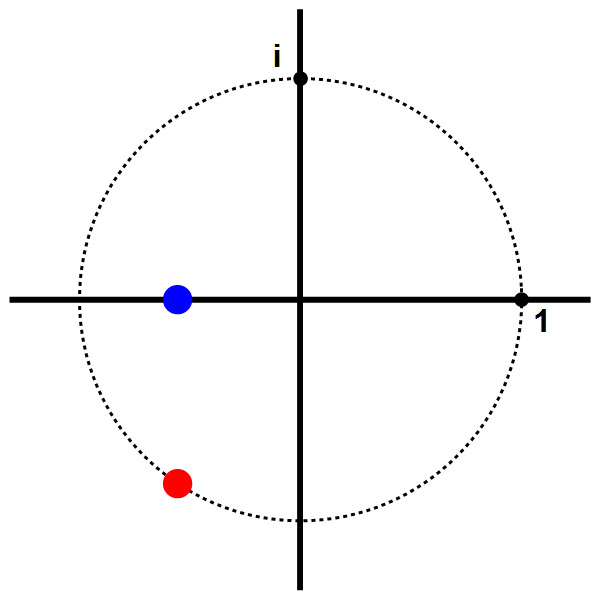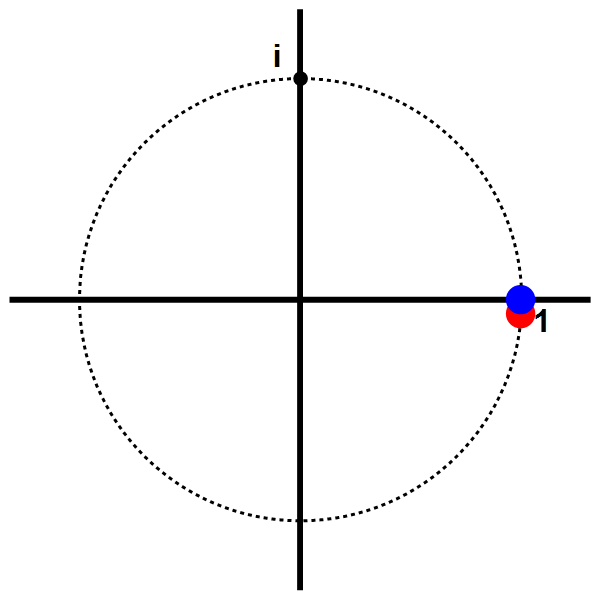
Afbeelding 2. Complex machtsverheffen.De rode stip toont het complexe getal 2^it als functie van de tijd t. De blauwe stip toont het reële deel van dit getal; dit getal trilt heen-en-weer in een sinus-beweging.

Als we nu alleen het reële deel van 2^it bekijken – de blauwe stip in de animatie – ziet we dat dit deel een regelmatige trilling uitvoert rond het getal 0. Nadere wiskundige bestudering laat zien dat deze trilling de vorm van een sinus heeft: de meest regelmatige golfvorm (ook wel een ‘vlakke golf’ genoemd) die er is. Dergelijke vlakke golven komen overal in de natuur voor: in watergolven, in de spanningsgolven die wisselstroom veroorzaken, in licht- en geluidsgolven, enzovoort.

Complexe getallen zijn daarmee dus erg nuttig om golfverschijnselen in de natuur te beschrijven. De vraag blijft echter: gaat het daarbij om een handige wiskundige truc, of kunnen we door complexe getallen te gebruiken ook echt iets nieuws leren? Dat dat laatste het geval is blijkt als we de bovenstaande functie vergelijken met de op het oog nauw verbonden functie

2^-t

Wie iets van de wiskunde van machtsverheffen weet, zal weten dat dit een functie is die, naarmate t toeneemt, een steeds kleinere waarde in de buurt van 0 krijgt. Met andere woorden: dit is het soort functie dat we gebruiken als er sprake is van demping in een systeem.

Demping en golfverschijnselen lijken op het eerste gezicht totaal verschillend. Toch zijn er allerlei systemen die bij een heel kleine verandering van de parameters overgaan van een trillende naar een gedempte toestand. Denk aan een gewicht dat we op een trampoline laten vallen: als de elasticiteit van de trampoline groot genoeg is zal het gewicht weer omhoog stuiteren, opnieuw omlaag vallen, enzovoort – een golfbeweging. Is de elasticiteit lager, dan wordt de val van het gewicht door de trampoline gebroken, maar stuitert het niet terug omhoog: een gedempte beweging. Als we reële getallen gebruiken, is het beslist niet direct duidelijk dat deze twee bewegingen sterk op elkaar lijken, maar met behulp van complexe getallen zien we dat meteen: de functie 2^-t heeft immers vrijwel dezelfde structuur als de functie 2^it. Het enige dat het verhogen van de elasticiteit dus doet is het veranderen van de exponent van een reëel naar een imaginair getal!

Afbeelding 3. Een schokdemper.Schokdempers worden gebruikt om trillingen te voorkomen. Toch is de wiskunde van demping en trillingen vrijwel hetzelfde, als we die bekijken door de bril van de complexe getallen. Afbeelding: Hans Brameier.

Relativiteit

Ook in de relativiteitstheorie van Albert Einstein spelen complexe getallen een belangrijke rol. Zoals in ons dossier over relativiteitstheorie uitgebreid valt te lezen, is het centrale idee uit deze theorie dat ruimte en tijd samen één vierdimensionaal geheel vormen: de ruimtetijd. De structuur van die ruimtetijd lijkt sterk op de structuur van de ruimte zelf, maar er zijn enkele belangrijke verschillen.

Eén zo’n verschil wordt duidelijk als we kijken naar de symmetrieën van de ruimtetijd. Laten we, om eenvoudig te beginnen, eens kijken naar de symmetrieën van alleen de ruimte. Onze ruimte heeft bijvoorbeeld translatie, oftewel verplaatsing, als symmetrie. Als we een natuurkundig experiment een meter naar links, rechts, boven of beneden opschuiven, zullen de uitkomsten ervan precies hetzelfde zijn. (Daarbij gaan we er natuurlijk van uit dat we alles wat invloed heeft op het experiment meeschuiven: als bijvoorbeeld het zwaartekrachtsveld van de aarde van belang is in het experiment, moeten we de hele aarde meeverschuiven.)

Ook in de ruimtetijd is translatie een symmetrie. Dat geldt zelfs voor een ’translatie’ in de vierde richting: een verschuiving in de tijd. Als we een bepaald experiment immers niet vandaag maar morgen uitvoeren, verwachten we exact dezelfde uitkomsten. (Ook hier weer: als alle andere omstandigheden die van invloed zijn op het experiment vandaag en morgen precies hetzelfde zijn.)

Een andere symmetrie die de driedimensionale ruimte heeft is ‘rotatie’, oftewel: draaiïng. Als we een experimentele meetopstelling een kwartslag draaien, verwachten we geen andere meetuitkomsten. Ook in de ruimtetijd kunnen we een meetopstelling natuurlijk een kwartslag draaien, maar we kunnen nu de vraag stellen: is het ook mogelijk om iets in de tijdrichting te ‘draaien’?

Afbeelding 4. Rotatie.Als we een natuurkundig systeem in de ruimte draaien, gelden in het gedraaide systeem exact dezelfde natuurwetten. Kunnen we iets echter ook in de tijdrichting ‘draaien’?

In eerste instantie is het absoluut niet duidelijk hoe we dat zouden moeten doen, maar hier biedt de wikunde van de complexe getallen uitkomst. Laten we eerst eens de volgende vraag stellen: als we iets draaien om een bepaald draaipunt, wat verandert er dan niet? Het draaipunt zelf verandert natuurlijk niet, maar belangrijker: van alle andere punten in ons systeem verandert de afstand tot het draaipunt niet. Als we het draaipunt coördinaten (0,0,0) geven, betekent dat (met behulp van de beroemde stelling van Pythagoras) dat voor iets wat zich oorspronkelijk op coördinaten (x,y,z) bevindt, de combinatie

x²+y²+z²

niet verandert – die combinatie is immers het kwadraat van de afstand tot (0,0,0).

Hoe zit dit nu in de ruimtetijd? In de ruimtetijd blijken afstanden niet meer vast bepaald te zijn: verschillende waarnemers kunnen het bijvoorbeeld oneens zijn over de lengte van een meetlat. Waar alle waarnemers het wel over eens blijken te zijn, is een bepaalde combinatie van ruimtelijke afstand en afstand in de tijd tussen twee gebeurtenissen. Die combinatie is

x²+y²+z²-(ct)²

Hierin staat de constante c voor de lichtsnelheid. Het zou te ver voeren om hier exact uit te leggen waarom alle waarnemers het over deze combinatie van coördinaten eens zijn, maar het bijzondere geval waarin deze combinatie 0 is, is eenvoudiger te begrijpen. In dat geval geldt namelijk dat

(ct)² = x²+y²+z²

In woorden: het kwadraat van de afstand tussen de twee gebeurtenissen (de rechterkant) is gelijk aan het kwadraat van de tijd maal de lichtsnelheid (de linkerkant). De tijd maal de lichtsnelheid is precies de afstand die een lichtstraal aflegt, dus deze formule zegt niets anders dan dat de waarnemers het eens zijn over de afstand die licht in een bepaalde tijd aflegt. Met andere woorden: voor iedereen is de snelheid van het licht hetzelfde – inderdaad een beroemd resultaat uit de relativiteitstheorie!

Net zoals rotaties afstand onveranderd laten, zijn de symmetrieën in de relativiteitstheorie dus de transformaties die de combinatie

x²+y²+z²-(ct)²

van coördinaten onveranderd laten. Dit zijn geen rotaties,maar ze lijken er wel heel erg op! Dat zien we nog beter als we de relatie i²=-1 gebruiken om de bovenstaande combinatie te schrijven als

x²+y²+z²+(ict)²

Kortom: de symmetrieën laten wel degelijk een ‘afstand’ onveranderd, en zijn dus wel degelijk ‘rotaties’, maar niet in de gewone coördinaten x, y, z en t, maar in coördinaten waarin de tijd wordt vermenigvuldigd met ic, en dus een complex getal is geworden!

Wat zijn deze symmetrieën precies? Verdere bestudering van de formules leidt tot het antwoord dat deze nieuwe ’tijdrotatie’-symmetrieën, uitgedrukt in onze oude coördinaten, zogeheten ‘boosts’ zijn. Dat wil zeggen: we nemen ons experiment, en geven het een bepaalde constante snelheid, bijvoorbeeld door het experiment in een rijdende trein uit te voeren. De wiskunde van de complexe getallen zegt dan dat de uitkomsten van het experiment niet zullen veranderen. Daarmee beschrijven complexe getallen dus heel elegant een ander beroemd principe uit de relativiteitstheorie: alle natuurwetten zijn precies hetzelfde voor stilstaande waarnemers en voor waarnemers die met constante snelheid bewegen!

Afbeelding 5. Een restaurant in de trein.In een trein die met constante snelheid beweegt zijn de natuurwetten precies hetzelfde als in een stilstaande trein. Daarom kunnen we in een trein een restaurant hebben: borden vallen niet van de tafel, koffie koelt precies even snel af, elektrische kookapparatuur werkt hetzelfde. enzovoort. Foto: Wikipedia-gebruiker JIP.

Volgende week

In het derde en laatste deel van deze mini-serie over complexe getallen bespreken we nog een laatste voorbeeld van hoe deze bijzondere getallen opduiken in de natuurkunde. Ook in de quantummechanica blijken complexe getallen namelijk van cruciaal belang te zijn. Nadat we ook dat voorbeeld hebben beschreven komen we terug op de vraag: zijn complexe getallen nu alleen een handig hulpmiddel voor de natuurkundige, of is onze natuur ook echt ‘complex’?

Het derde en laatste artikel in deze serie verschijnt op dinsdag 22 maart.