
Naast de getallen die we in het dagelijks leven tegenkomen – denk hierbij bijvoorbeeld aan de gehele getallen 1, 2, 3, … om dingen te kunnen tellen, maar ook aan meer ingewikkelde kommagetallen of het getal dat tevoorschijn komt bij cirkelberekeningen – zijn er ook meer ‘exotische’ getallen die je waarschijnlijk wat minder vaak tegenkomt. Een voorbeeld zijn imaginaire getallen die tevoorschijn komen zodra je bepaalde vergelijkingen probeert op te lossen. Op de middelbare school wordt vaak gezegd dat de volgende vergelijking geen oplossingen heeft:
\( x^2 = -1 \).
Dit komt doordat een getal in het kwadraat nooit negatief kan worden (min keer min is immers plus!) Deze uitspraak is waar voor de reële getallen die we normaal gesproken gebruiken. Het idee is nu om een nieuw getal te introduceren dat deze vergelijking wél oplost. We introduceren daarom het getal \( i \) met de volgende eigenschap:
\( i^2 = -1 \).
We hebben de gebruikelijke reële getallen nu uitgebreid met het imaginaire getal \( i \); de getallen die je op deze manier kunt maken – door reële en imaginaire getallen te combineren – noemen we complexe getallen. Ieder complex getal is daarmee te schrijven op de volgende manier:
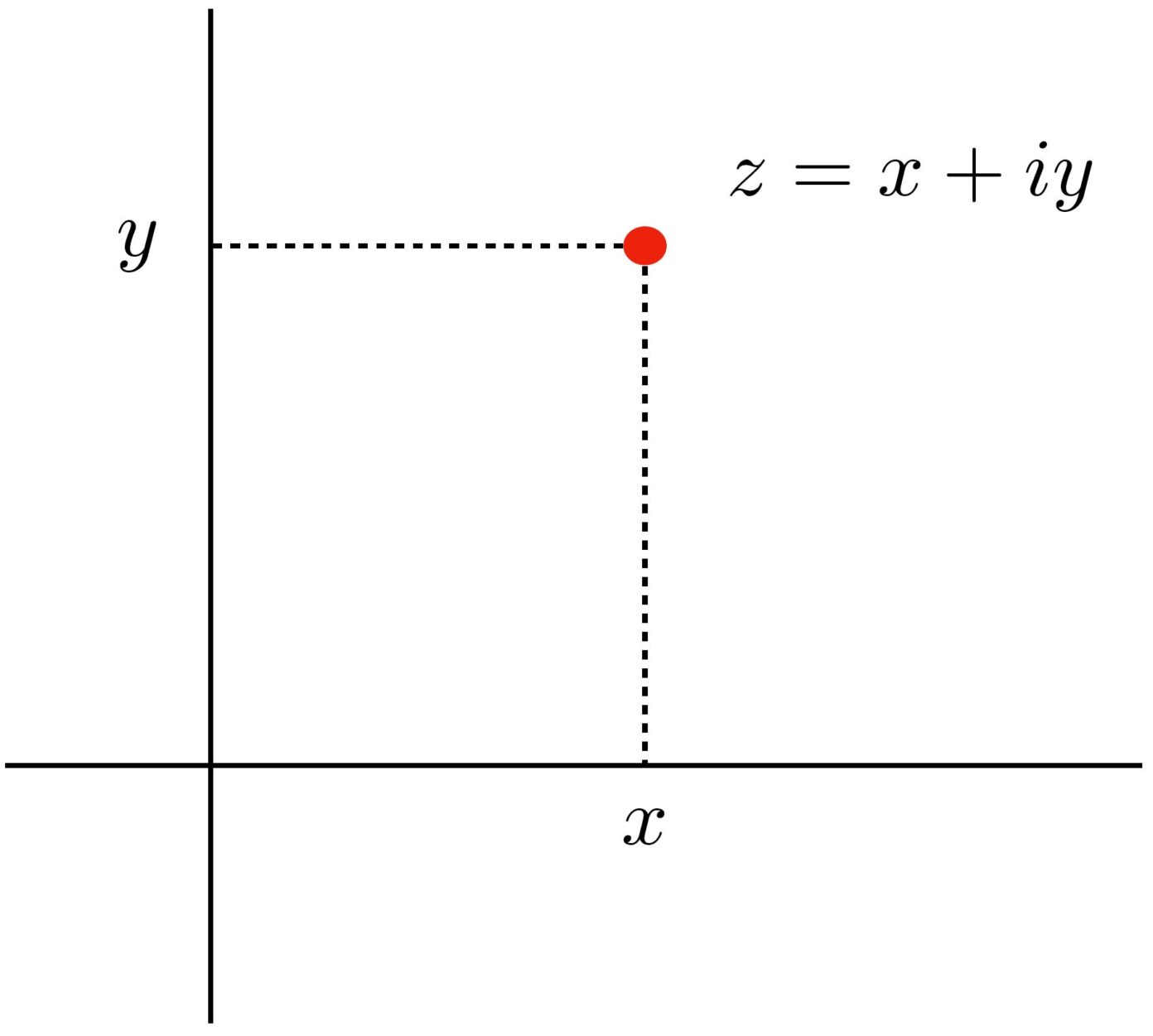
\( z = x + i y \).
Hier zijn x en y reële getallen, die respectievelijk het reële en imaginaire deel van z worden genoemd. Op deze manier kunnen we over complexe getallen nadenken in termen van punten in een vlak: de x-en y-coördinaten van dit punt worden precies gegeven door de coëfficiënten in de bovenstaande formule. Het complexe vlak is daarmee een mooi hulpmiddel om op een meetkundige manier over complexe getallen na te denken. Merk op dat de gebruikelijke reële getallen maar een klein deel van het complexe vlak beslaan: ze liggen op de x-as, oftewel: het zijn de punten met y = 0.
Deze uitbreiding van reële naar de complexe getallen is voor de niet-ingewijde lezer wellicht wat abstract. Waar kunnen deze ‘imaginaire’ getallen nou goed voor zijn? Verrassend genoeg blijken complexe getallen van essentieel belang in onze huidige beschrijving van de natuur. Zo rust de gehele quantummechanica – de natuurkundige theorie die de natuur in het klein beschrijft – op het gebruik van complexe getallen. Het lijkt er daarmee op dat de natuur op een fundamenteel niveau wel degelijk gebruik maakt van complexe getallen!
Laten we nu gaan naar het onderwerp van dit artikel: de Juliaverzameling. De definitie van deze verzameling volgt uit de formule
\( z_n = z_{n-1}^2 + c \).
De bovenstaande vergelijking kun je als volgt interpreteren: beginnend met een bepaald complex getal z0 kunnen we het voorschrift gebruiken – door het aan de rechterkant in te vullen – om een nieuw complex getal z1 – aan de linkerkant – te maken. De truc is nu om het getal z1 opnieuw aan de rechterkant in te vullen, en het resultaat daarvan noemen we z2. Door dit proces oneindig vaak te herhalen vinden we een rijtje van complexe getallen:
\( z_0, z_1, z_2, z_3, \ldots \).
Wat is het gedrag van de getallen zn als n heel groot wordt? Dit hangt natuurlijk af van de beginwaarde z0. Je kunt bewijzen dat voor de meeste waarden van z0 het bovenstaande rijtje van complexe getallen onbegrensd groeit1. Voor bepaalde waarden van z0 springen de getallen in het rijtje ook heen en weer in het complexe vlak, maar op zo’n manier dat ze binnen een bepaald gebied blijven: ze zitten daar als het ware gevangen. De verzameling van alle z0 waarvoor het bovenstaande rijtje op die manier begrensd is, heet de Juliaverzameling, naar de wiskundige Gaston Julia. Als je al deze waarden van z0 in het complexe vlak zou weergeven krijg je tweedimensionale plaatjes – waarvan een voorbeeld (voor een bepaalde waarde van de constante c) in afbeelding 3 is te zien.
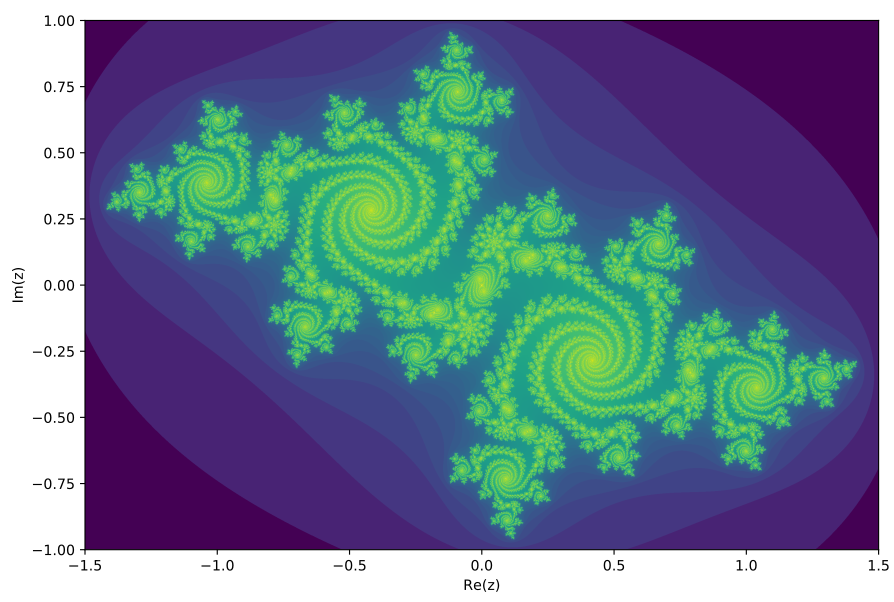
Het is aardig om de rand van de Juliaverzameling in wat meer detail te bekijken. Die bestaat uit precies de grensgevallen waarbij het rijtje net wel naar oneindig ontsnapt. Het blijkt dat deze rand een enorm rijke structuur heeft: zodra je ergens op de rand inzoomt vindt je nieuwe patronen die erg veel weg hebben van de originele Juliaverzameling, maar er toch steeds weer net anders uitzien. Ook houdt de mate van detail nooit op: je vindt met iedere schaalverkleining weer iets nieuws. Wiskundigen noemen een meetkundig object met dergelijke eigenschappen een fractal – een patroon met oneindig veel detail dat zichzelf op steeds kleinere schaal bij benadering herhaalt. Als je meer over fractals te weten wilt komen, kun je een van mijn vorige artikelen hierover raadplegen: daarin leg ik in meer detail uit wat fractals zijn, en wat deze patronen te maken hebben met bijvoorbeeld sneeuwvlokjes en broccoli.

Kortom: we hebben gezien hoe een simpele vergelijking voor complexe getallen aanleiding kan geven tot enorm complex gedrag. De Juliaverzameling bestaat uit alle complexe getallen die bij het herhaald invullen van een specifieke formule binnen een bepaald gebied gevangen blijven zitten. De rand van deze verzameling beschrijft een patroon met oneindig veel detail, door wiskundigen ook wel een fractal genoemd. Juliaverzamelingen zijn daarmee een interessant voorbeeld van hoe complexe getallen in de wiskunde worden gebruikt. Al met al: een complex, maar boeiend verhaal.
Wil je meer weten? In het onderstaande filmpje wordt in meer detail uitgelegd wat de Juliaverzameling en de nauw verwante Mandelbrotverzameling zijn.
[1] We bedoelen hiermee dat de absolute waarde van het complexe getal – dat wil zeggen de afstand van het punt in het complexe vlak tot de oorsprong – naar oneindig gaat.