
In dit artikel:
Het raadsel
Wat is de wiskundige definitie van een bit aan informatie?
Wat is de wiskundige definitie van Shannon-entropie? (En van de binaire entropiefunctie?
Bonus: hoe hielp Informatietheorie mij om het raadsel op te lossen?
Informatietheorie in de natuurkunde en het raadsel
In de jaren rondom de conceptie van de thermodynamica van zwarte gaten is men gaan onderzoeken in hoeverre zwaartekracht op te vatten valt als emergent fenomeen. Op deze website is een aantal artikelen over dit onderwerp te vinden: 1, 2, 3. In mijn masterscriptie doe ik onderzoek naar de vraag in hoeverre quantumcomputers ons kunnen helpen met het experimenteren aan dergelijke theorieën. Alhoewel de kwestie van quantumzwaartekracht mooi genoeg is om pagina’s tekst te verdienen, richten we nu onze aandacht op het volgende raadsel:
Paardenraces: je hebt 25 paarden en een renbaan met 5 startplekken. Door de renbaan te gebruiken weet je de volgorde waarin de vijf paarden zijn gefinisht – maar je weet niet de exacte tijden. Je wilt erachter komen wat je snelste drie paarden zijn, en in welke volgorde. Wat is het kleinste aantal keren dat je de renbaan moet gebruiken om met zekerheid achter de top drie te komen?
Een bit aan informatie
Om mijn oplossing van dit raadsel te formuleren heb ik de informatietheorie gebruikt. De theorie is onder andere ontwikkeld om fundamentele limieten op communicatie te bepalen, gegeven dat het communicatiekanaal een beetje ruis heeft. De ruis wordt vaak geformaliseerd via een kansproces, en daarmee vormt de kansrekening een fundament voor de definitie van informatie.
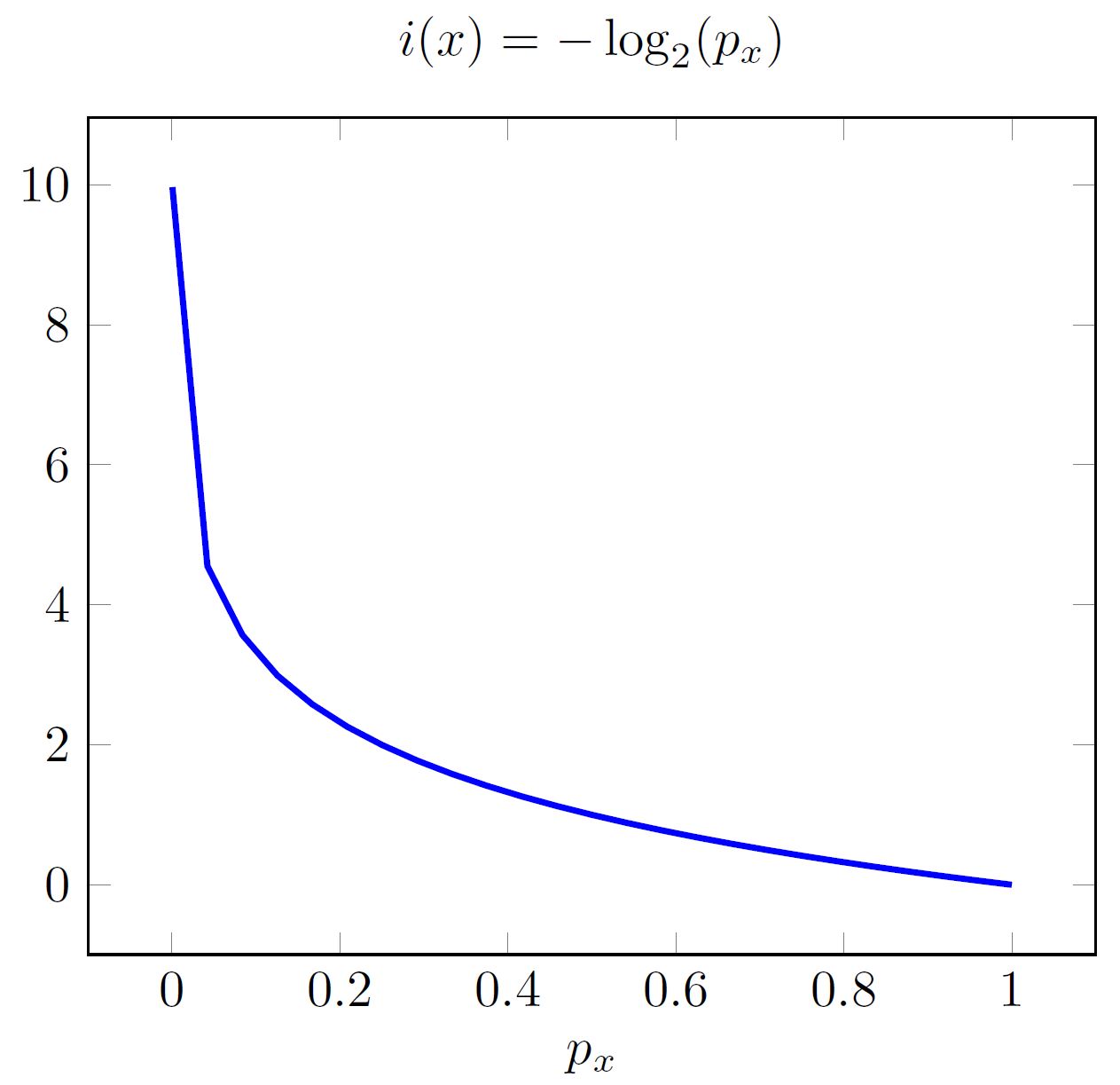
De hoeveelheid informatie \( i(x) \) die bevat is in de uitkomst \( x \) van een experiment met willekeurige uitkomsten hangt af van de kans op die uitkomst. In een formule: als de kans op de uitkomst \( x \) gelijk is aan \( p_x \), dan wordt de informatie gedefinieerd als
\(i(x)=-\log_2(p_x).\)
De logaritme met grondtal 2 impliceert dat de grootheid \( i(x) \) gemeten wordt in bits. Hoe relateert dit aan ons alledaagse begrip van bits? Wanneer je een munt opgooit krijg je de uitkomst \( x=\text{munt} \) met een kans \( p_x=0{,}5\). Je kan dan nagaan dat de hoeveelheid informatie gelijk is aan 1 bit: \( i(\text{munt})=1~\text{bit}\). Neem twee muntjes: de hoeveelheid informatie in het gooien van kop en kop (met kans \( 0{,}25 \)) is dan 2 bits. Dit generaliseert: in de uitkomst van het opgooien van \(N\) muntjes zitten \( N~\text{ bits}\) aan informatie.
Toch moet je voorzichtig zijn met de analogie. Wanneer je plots een oneerlijk muntje hebt gekregen waarvoor de kans op \( x=\text{munt}\) gelijk is aan \( p_x=0{,}25 \) (en de kans op \( y=\text{ kop}\) dus \( 1-p_x=0{,}75 \)) is de informatie \( i(x)= 2\) als je tóch munt gooit – ondanks dat we maar 1 muntje hebben! Hoe zit dat?
De informatie \(i(x)\) in een uitkomst \(x \) kan gezien worden als een mate van verrassing: hoe groter \(i(x)\), hoe verrassender de uitkomst. Dit is ook duidelijk als ik de hoeveelheid informatie plot tegenover de kans, zoals in afbeelding 1 gedaan is. De hoeveelheid informatie in een proces waarvan de uitkomst vooraf al vastligt (dus met kans \( p_x=1 \) op één uitkomst \( x \)) is nul! Dit noemen we een deterministisch proces.
Shannon-entropie en de binaire entropiefunctie
Entropie \( S \) is een grootheid die vooral bekend is uit de thermische fysica: entropie is een maat voor het aantal microscopische toestanden \( \Omega \) dat hoort bij een bepaalde macroscopische toestand (\( S=k_\text{B} \ln\Omega\), zie ook 1 en 2, en voor de geschiedenis achter het begrip 3). In zekere zin karakteriseert entropie onze onwetendheid over een systeem: we weten bijvoorbeeld niet hoe elk deeltje in een gas beweegt, maar er is toch enig begrip door met het emergente fenomeen temperatuur te duiden hoe snel de deeltjes in een gas gemiddeld bewegen. Omgekeerd horen bij één temperatuur heel veel mogelijke configuraties van snelheden voor de individuele deeltjes, en dat aantal wordt bepaald door de entropie.
Ook voor kansprocessen bestaat een definitie van entropie: de zogeheten Shannon-entropie. De wiskundige definitie van die Shannon-entropie is als volgt: laat \( x_1, x_2, x_3, \ldots, x_N\) uitkomsten zijn die willekeurig verdeeld zijn met bijbehorende kansen \( p_1, p_2, p_3, \ldots, p_N\). Dan is de Shannon-entropie \( H \) gegeven door:
\( H = \sum_{n=1}^N p_n i(x_n)= -\sum_{n=1}^N p_n\log_2(p_n). \)
De eerste gelijkheid toont aan dat de Shannon-entropie niets meer of minder is dan een gewogen gemiddelde van de informatie in een systeem dat probabilistisch is. In de tweede gelijkheid heb ik de definitie van informatie \( i(x) \) ingevuld – controleer die stap vooral zelf. Merk op dat Shannon-entropie ook de eenheid bits heeft: het is immers een gewogen gemiddelde van \( i(x)\), uitgedrukt in bits.
Voorbeeld 1: Laten we de definitie beter begrijpen aan de hand van een voorbeeld: de munt die wordt opgegooid. Wat is de Shannon-entropie die bij deze munt hoort? De uitkomsten zijn \( x_1=\text{kop}, x_2=\text{munt}\), beide met kans \( p_1=p_2=0{,}5\). Invullen van die getallen geeft:
\( H=-p_1\log_2(p_1)-p_2\log(p_2)= -\frac{1}{2} \times (-1) – \frac{1}{2} \times (-1) = 1 ~\text{bit}. \)
Voorbeeld 2: Hoe zit het met de oneerlijke munt? In dat geval blijft alles hetzelfde behalve dat de kans op kop niet identiek \( 0{,}5 \) is maar een willekeurig getal tussen nul en één dat ik \( p \) noem. Automatisch is de kans voor munt (en dus niet kop) vastgesteld op \( 1-p \). Dit geeft de binaire entropiefunctie
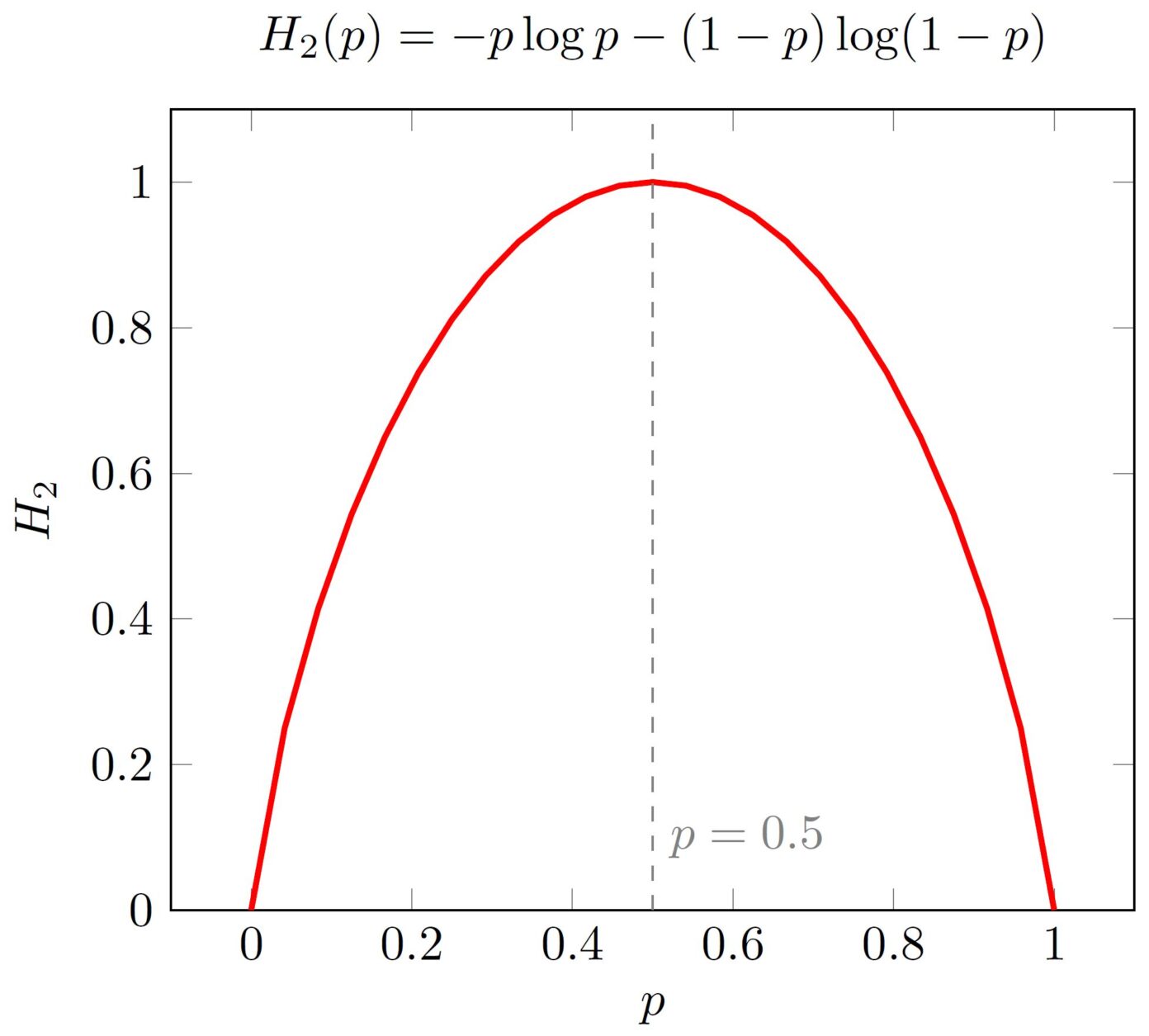
\( H_2(p) = -p\log_2(p)-(1-p)\log_2(1-p). \)
De ‘2’ aan de linkerkant schrijven we om aan te geven dat het gaat om twee mogelijke uitkomsten – vandaar ook de naam binaire entropiefunctie. Voor \( p= 0{,}5 \) vinden we terug dat \( S(0{,}5)=1 \), zoals we zouden verwachten.
De binaire entropiefunctie is weergegeven in afbeelding 2 als functie van \(p\). Merk op dat de functie piekt bij \( p=0{,}5 \) (de uniforme verdeling – hierover later meer). Ten slotte is het te zien dat de Shannon-entropie identiek nul is bij een deterministisch systeem. Er is dan immers geen verrassing, dus ook het gewogen gemiddelde van de informatie moet nul zijn.
Voorbeeld 3 (Uniforme verdeling): De binaire entropiefunctie wordt zoals we gezien hebben maximaal voor een verdeling waarbij de twee kansen gelijk zijn (namelijk \(0{,}5\)): dit heet een uniforme kansverdeling met twee uitkomsten. In het algemeen, met \(N\) uitkomsten, is de uniforme verdeling van \( N\) kansen er een waar alle kansen gelijk zijn aan \(1/N\). Denk bijvoorbeeld aan een eerlijke dobbelsteen, waar \( N = 6 \) en alle kansen gelijk aan \( 1/6 \). Je kan dan berekenen wat de Shannon-entropie voor een uniforme verdeling is:
\( H(\text{ uniform })=-\sum_{n=1}^N\frac{1}{N}\log_2(1/N)=-\log_2(1/N)=\log_2(N) ~\text{bits}. \)
Dit is exact de hoeveelheid bits die nodig is om de \( N \) uitkomsten te kunnen weergeven!
Knipoog naar Zwarte Gaten: de formule van Bekenstein-Hawking zegt dat de entropie van een zwart gat van een zonnemassa ongeveer van de ordegrootte \(S\sim10^{54}~\text{J/K}\) is. Dit komt overeen met een Shannon-entropie van \(H\sim 10^{78}~\text{bits} \). Volgens het holografisch principe kun je de entropie van een zwart gat zien als de informatie in een theorie die de rand van dat zwarte gat beschrijft (zie ook zwarte gaten en entropie). Dat zijn een hoop nullen en ééntjes die je op die event horizon moet voorstellen!

Bonus: informatietheorie helpt met het raadsel
Tot slot gaan we terug naar het raadsel met de 25 paarden en renbaan met 5 plekken. Heb je het al opgelost? Als je bedenkt dat de paarden in beginsel allemaal evenveel kans hebben om de snelste te zijn (een uniforme verdeling), dan is de Shannon-entropie van dit systeem maximaal: er is maximale onzekerheid. Nu is het aan jou om de Shannon-entropie in zo min mogelijk stappen naar nul te brengen: dan weet je het antwoord met zekerheid (deterministisch). Dit kan je doen door keuzes te maken die de meeste informatie \( i(x) \) bevatten – zie deze video vanaf 8:09 die voor een ander, vergelijkbaar raadsel uitlegt waarom dit de beste keuze is.
Dit toont aan dat je het beste eerst simpelweg de vijfentwintig paarden kan laten rennen in je eerste vijf rondes: na je eerste ronde ben je nog maximaal onzeker over de overige twintig, dus maximaliseert de informatie wanneer je vijf paarden uit deze twintig laat rennen (enzovoort). Dit geeft je dus de beste eerste vijf stappen.
Ik zal de lol van het raadsel niet verpesten door de laatste twee stappen te verklappen!
Ten slotte
Hoe gaan paardenraces ons helpen met het oplossen van de raadsels rond quantumzwaartekracht? Helaas weet ik het antwoord daar niet meteen op, maar hopelijk heb ik je iets bijgebracht over de begrippen informatie (gelinkt aan verrassing) en Shannonentropie – en die begrippen spelen een heel belangrijke rol in het moderne onderzoek naar quantumzwaartekracht. Veel plezier met het oplossen van het raadsel – ik hoor het graag als je nog een ander raadsel vindt waarbij de intuïtie van informatietheorie helpt!
[1] Met dank aan Martijn Pellegrom voor het voorstellen van het raadsel.
QU is sinds kort weer actief op Instagram! Volg ons voor nieuws en aankondigingen van nieuwe artikelen: https://www.instagram.com/quantumuniverse.nl/