Zulk gedrag kan chaotisch zijn, of het kan gebeuren dat er verschillende ‘fasen’ zijn waarin het systeem zich kan bevinden. Eén manier om te laten zien hoe complexe systemen chaotisch gedrag kunnen vertonen, is door te kijken naar het gedrag van de oplossingen. Gelukkig kunnen we daar ook al veel over zeggen in de gevallen waarin een vergelijking niet oplosbaar is. Zo is er het concept van een bifurcatie: door parameters in een systeem te veranderen, zullen de oplossingen kwalitatief heel anders zijn. Een heel mooi voorbeeld wat ik in dit artikel wil illustreren, is het concept van limietcykels. Dit doe ik aan de hand van een eenvoudig maar rijk voorbeeld uit de biofysica: het jager-prooimodel.
Het jager-prooimodel en limietcykels
Het jager-prooimodel, ook wel de Lotka–Volterravergelijkigen genoemd, is een model van wiskundige vergelijkingen waarbij twee types ‘populaties’ beschreven worden: de jagers en de prooi. Het doel is te beschrijven hoe deze twee populaties samenleven. Laten we eerst een simpel geval bekijken aan de hand van een paar aannames. Zo nemen we bijvoorbeeld aan dat de prooi altijd voldoende te eten heeft om zich voort te planten. De vorm van de Lotka-Volterravergelijkingen is dan vrij eenvoudig te beredeneren. Dit doen we als volgt: Laten we de populatie (het aantal levende exemplaren) van de prooi ‘x’ noemen, en de populatie van de jagers ‘y’. Als de jagers niet op de prooi jagen, dan zou de prooi natuurlijk ongelimiteerd groeien: voor hen is er immers geen tekort aan eten. De jagers daarentegen hebben in dat geval een probleem, want die hebben geen eten. Hun populatie zal dus afnemen. Nu nemen we aan dat in dit geval de snelheid waarmee de populaties groeien of afnemen afhankelijk is van de huidige totale populatie (dat wil zeggen: een vast percentage van de bestaande populatie wordt geboren of sterft juist), met een evenredigheidsconstante α voor de prooi, en –γ (met een minteken, de populatie neemt immers af) voor de jagers. De populaties groeien dan volgens de volgende vergelijkingen:
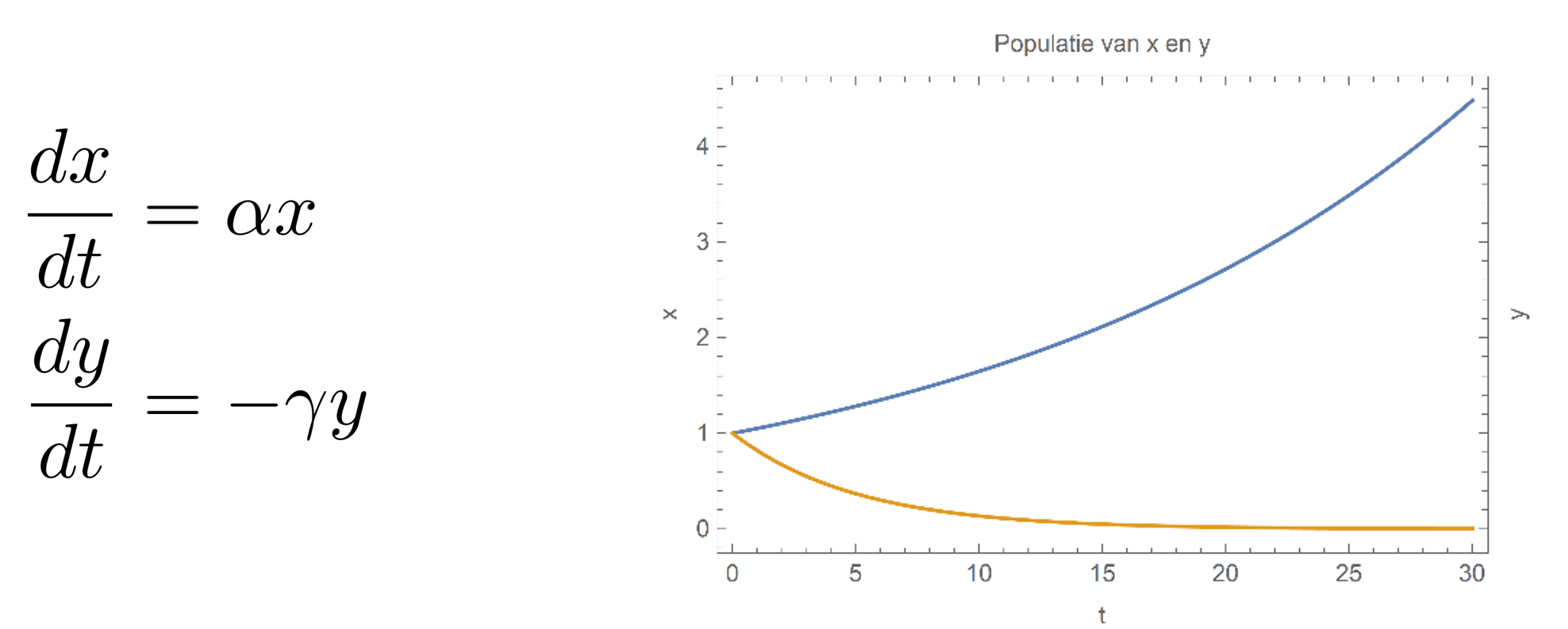
Uiteraard is het de bedoeling dat de jagers wél gaan jagen op de prooi! Als we dat toelaten hebben de jagers wel te eten, en kan de populatie van jagers dus weer toenemen. Als we nu aannemen dat elke jager in contact kan komen met elke prooi op ieder tijdstip, dan verandert de jagerspopulatie evenredig met zowel ‘x’ als ‘y’ (dus met het product), met een evenredigheidsconstante δ. Hetzelfde geldt voor de prooipopulatie ‘x’, maar die gaat natuurlijk juist áfnemen, met een evenredigheidsconstante die we β noemen. De volledige set van vergelijkingen is dan als volgt:
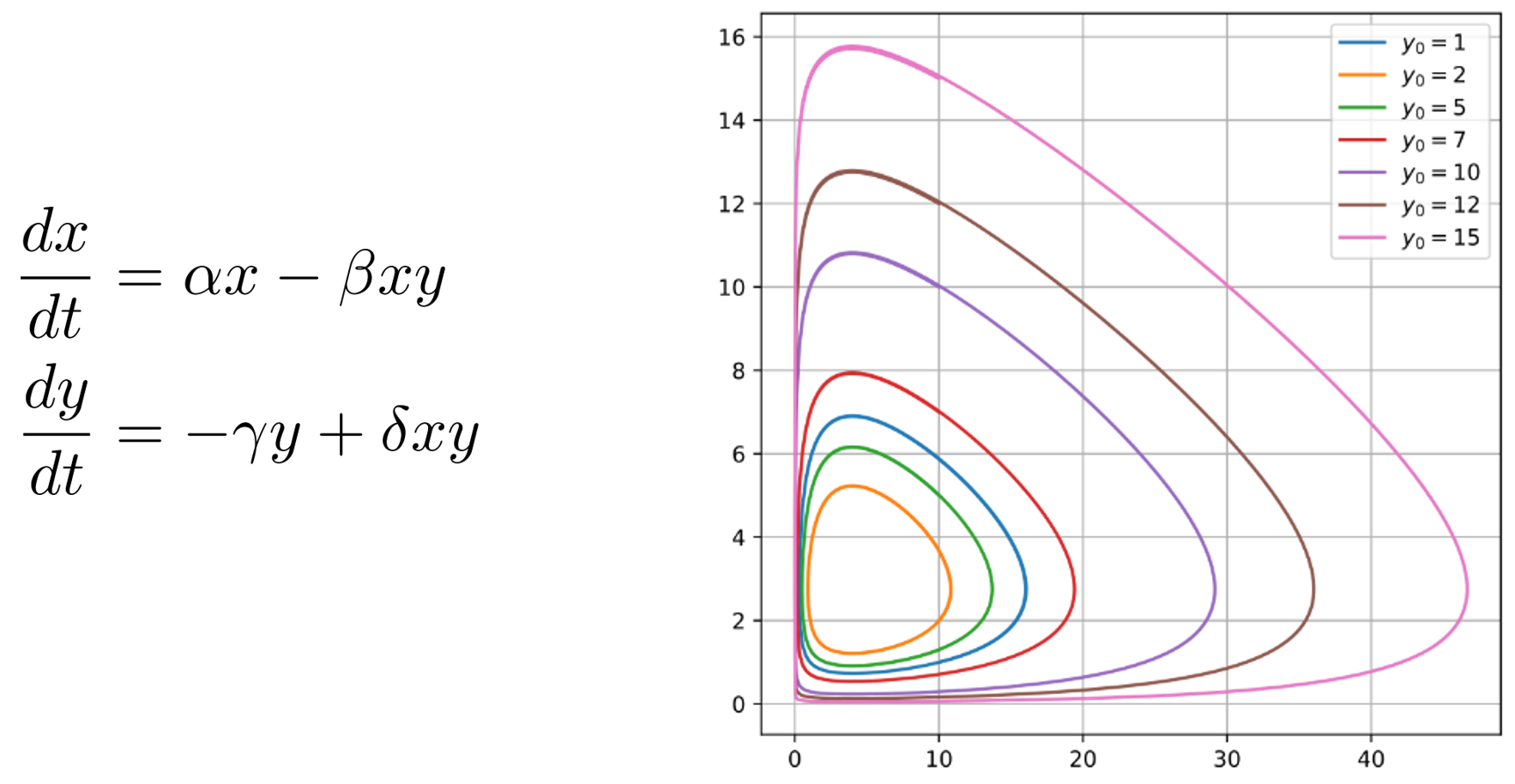
Let weer op het verschil van de plus- en mintekens; de jagers gaan er in populatie op vooruit als er gejaagd wordt, en de prooi juist erop achteruit. Het blijkt dat de oplossingen van dit systeem altijd de vorm hebben van ‘oscillaties’ tussen de twee populaties. Als de ene populatie heel groot is, zal dat een effect hebben op de andere populatie. Die zal dan toe- of afnemen, afhankelijk van of het om de jager of de prooi gaat. (Bijvoorbeeld: als er veel jagers zijn hebben die elk relatief weinig te eten, en neemt de populatie dus af.) Dit is voor een aantal voorbeelden te zien in de grafiek in afbeelding 2. De oscillaties die we daar zien heten ook wel ‘limietcykels’. Zulke cykels zijn meta-stabiele toestanden van het systeem: wanneer de begintoestand iets afwijkt van een situatie op de limietcykel, zal het systeem vanzelf naar de cykel toevloeien, en daar blijven oscilleren als een stabiele toestand. In dit voorbeeld is de situatie nog relatief eenvoudig, maar het blijkt dat limietcykels ook vele malen complexer kunnen worden.
Een complexer voorbeeld
De vergelijkingen die we hierboven gezien hebben zijn een voorbeeld van een gekoppeld, dynamisch systeem. Op zich is dat systeem nog eenvoudig op te lossen en vereist het vrij weinig wiskundige trucs. Het blijkt echter dat een variatie van het jager-prooimodel van hierboven een rijker verhaal vertelt. Deze variatie wordt gegeven door de volgende vergelijkingen:
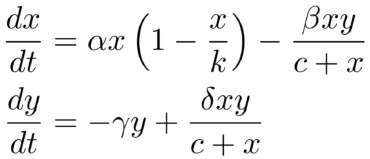
Het bovenstaande systeem is in grote mate hetzelfde als het vorige, alleen zijn er nu twee extra parameters. Zo zorgen we ervoor dat er een maximum populatie van de prooi (x) kan zijn door middel van een nieuwe parameter k. Je ziet in de vergelijking dat als x gelijk is aan k, de groeiterm voor de prooi x gelijk wordt aan 0. Daarnaast controleren we de consumptiesnelheid (hoe snel wordt de prooi gevangen wordt door de jager) voor het geval de populatie van x klein is. Als we het systeem in detail onderzoeken zien we een aantal interessante fenomenen. Afhankelijk van de keuze van de parameters α, β, γ, δ, k en c kan het systeem zich verschillend gedragen. Zo kan het gebeuren dat het aantal jagers en prooien simpelweg niet verandert in de loop van de tijd: de toename van beide populaties is evenveel als de afname. Waardes waarvoor dit gebeurt zijn eenvoudig te vinden door het volgende te stellen: als het systeem zo in evenwicht is, dan veranderen de waardes van ‘x’ en ‘y’ niet in de loop van de tijd. De linkerkant van de vergelijkingen in afbeelding 3 is dan dus gelijk aan nul. Dit levert een betrekkelijk eenvoudig op te lossen systeem van vergelijkingen op.
We moeten wel goed opletten met wat we met een dergelijke oplossing nu eigenlijk berekend hebben. Het feit dat een bepaalde combinatie van waardes een evenwicht oplevert (toename gelijk aan afname), wil niet zeggen dat het systeem ook daadwerkelijk in een stabiel evenwicht is. Wat gebeurt er bijvoorbeeld als onze begintoestand héél klein beetje van de evenwichtstoestand afwijkt? Zoiets kan in de natuur altijd gebeuren: een extra prooi kan toevallig overlijden, of een extra jager kan toevallig overleven. Als we vanuit deze iets afgeweken begintoestand weer ‘terugvloeien’ naar de oorspronkelijke evenwichtstoestand, dan is er sprake van een stabiel evenwicht. Omgekeerd echter: als een minimale afwijking het systeem steeds verder wegdrukt van de evenwichtstoestand, dan is het instabiel. Vergelijk die situatie met een bal die je op de top van een heuvel legt, en de eerdere situatie met een bal in het dal tussen twee heuvels. Als je de bal op de top van de heuvel een heel klein beetje verplaatst, dan rolt hij vanzelf naar beneden: er is een instabiele evenwichtstoestand. In het dal is de toestand juist stabiel, omdat een kleine afwijking geen effect heeft op de plek waar de bal uiteindelijk zal eindigen: op het laagste punt. De vraag of een evenwichtstoestand stabiel is kan beantwoord worden met een wiskundige techniek die lineaire stabiliteitsanalyse heet. Op de details gaan we hier verder niet in, maar het belangrijkste resultaat van een dergelijke analyse is dat we diagrammen kunnen maken die ons vertellen voor welke waardes van de systeemparameters ons systeem stabiel of instabiel – zie bijvoorbeeld afbeelding 4.
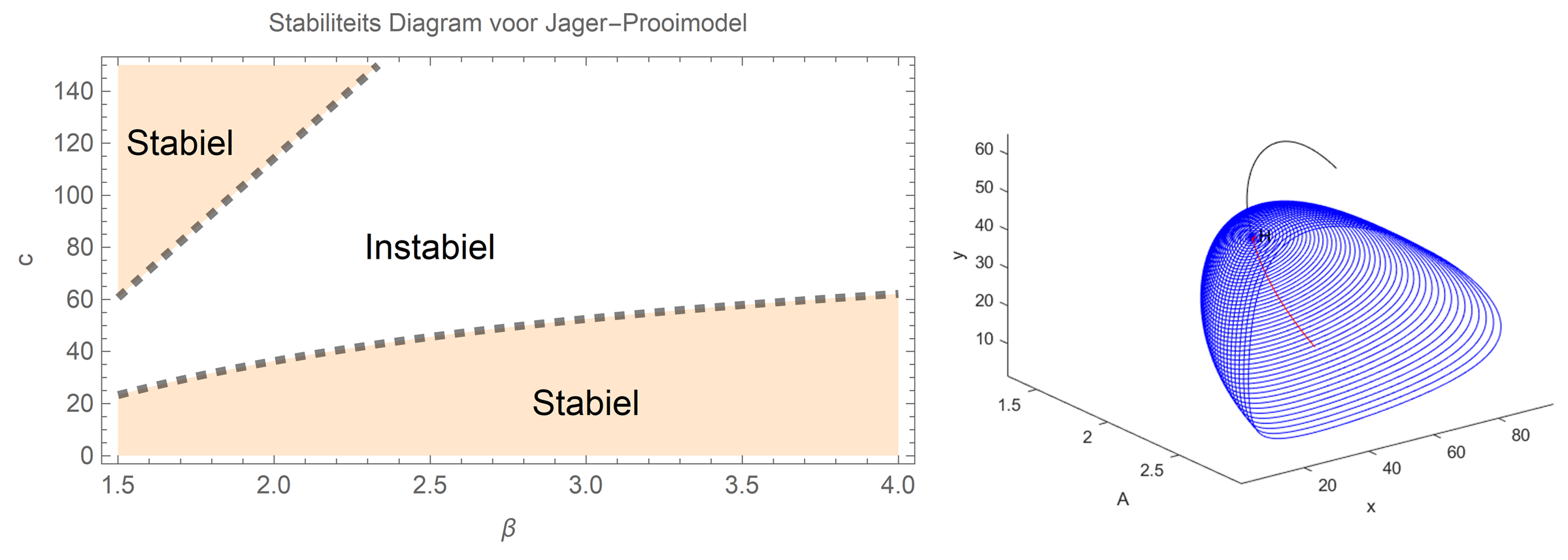
Bifurcaties
Nu is er nog een laatste vraag over: wat gebeurt er in de gevallen waar er een instabiel evenwicht is? Zullen de jagers of de prooien uitsterven, of zullen de populaties oneindig toenemen? In principe zijn beide situaties mogelijk, maar in dit geval gebeurt er iets wat we al eerder hebben gezien: het systeem komt terecht in een toestand van een limietcykel! Eigenlijk ondergaat het systeem een ‘fase-overgang’ waarbij het gaat van een stabiele evenwichtstoestand naar een eeuwig oscillerende toestand. Dit gebeurt bijvoorbeeld als we de reproductiesnelheid van de prooi een beetje aanpassen, zoals te zien in afbeelding 4b. Hoe de uiteindelijke oscillatie er precies uitziet is te zien in afbeelding 5 hieronder.
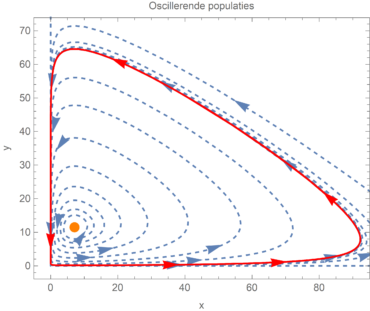
Het is opmerkelijk dat een systeem van twee vergelijkingen dat met heel eenvoudige argumenten opgesteld is, al zoveel informatie kan bevatten. Het proces dat in dit artikel beschreven is, is uiteraard al grondig bestudeerd. Het geval waarbij een systeem van een stabiele naar een instabiele toestand met limietcykels kan gaan, heet ook wel een bifurcatie. ‘Bifurcatie’ is de algemene naam voor een fenomeen waar de oplossingen zich plotsklaps anders gaan gedragen als parameters van het systeem aangepast worden – een soort faseovergang, dus. In dit specifieke systeem heeft de bifurcatie zelfs een speciale naam: een ‘Hopf-bifurcatie’, genoemd naar de wiskundige die dit type bifurcatie geclassificeerd heeft.
Bifurcaties zijn zeer interessante fenomenen. Het ‘splitsen’ van oplossingen van een systeem blijkt sterk gerelateerd aan het concept van chaos. Het concept van chaos is van groot belang voor de natuurkunde. Zo wordt er gesteld dat het ontstaan van chaos te maken heeft met thermalisatie van systemen, iets wat momenteel gezien wordt als een belangrijke link tussen klassieke thermodynamica, en quantummechanica. Daarnaast heeft het concept van chaos ook andere interessante toepassingen. Om maar een voorbeeld te noemen: er is aangetoond dat chaotische systemen gebruikt kunnen worden om veilige encryptie-sleutels te versturen tussen twee personen. Chaos, thermalisatie en versleuteling zijn de bouwstenen van een heel nieuw verhaal, en die bewaren we dus voor een toekomstig artikel.