
Volgens Einsteins algemene relativiteitstheorie zorgt massa voor een kromming van de ruimtetijd. Als gevolg hiervan bewegen andere massa’s zich in gekromde banen, een fenomeen dat wij kennen als ‘zwaartekracht’. Centraal in de algemene relativiteitstheorie staan de Einsteinvergelijkingen: tien vergelijkingen die de relatie tussen de verdeling van massa in de ruimtetijd en de kromming van diezelfde ruimtetijd beschrijven. Een oplossing van de Einsteinvergelijkingen is een meetkundige vorm (metriek) van de ruimtetijd die in overeenstemming is met de aanwezige massa. Met behulp van de metriek kan vervolgens berekend worden hoe de gekromde banen van objecten in de ruimtetijd eruitzien.
Singulariteiten
In het algemeen is het erg moeilijk om een oplossing te vinden van de Einsteinvergelijkingen. Hoewel die vergelijkingen inmiddels ruim honderd jaar oud zijn, is het aantal oplossingen dat gevonden is dan ook beperkt. Karl Schwarzschild schreef in 1916 als eerste een oplossing van de Einsteinvergelijkingen op. Zijn Schwarzschildmetriek beschrijft de ruimtetijd rondom een zwart gat. De metriek heeft een bijzonder punt – de singulariteit – waar de ruimtetijd volgens Einsteins vergelijkingen oneindig krom wordt. Dit verschijnsel is niet uniek voor Schwarzschilds oplossing: ook andere, later gevonden, oplossingen van de Einsteinvergelijkingen hebben singulariteiten.
De oneindigheden in de relativiteitstheorie zijn op zijn zachtst gezegd merkwaardig. Lang werd dan ook getwijfeld of singulariteiten – en in het verlengde daarvan: zwarte gaten – echt konden bestaan, of dat het slechts wiskundige artefacten van de theorie waren. De twijfel werd niet in de laatste plaats ondersteund door het feit dat de meeste bekende oplossingen van Einsteins vergelijkingen veel symmetrie hebben – denk bijvoorbeeld aan een ruimtetijd die er in elke richting exact hetzelfde uitziet. Zo’n hoge mate van symmetrie komt niet overeen met de natuur die wij om ons heen zien.
In 1965 bewees Nobelprijswinnaar Roger Penrose dat singulariteiten in zwarte gaten daadwerkelijk gevormd kunnen worden, ook als de ruimtetijd niet erg symmetrisch is. Sterker nog, Penrose bewees dat singulariteiten gevormd móéten worden als er maar voldoende massa in een bepaalde hoeveelheid ruimte terechtkomt. In de jaren die volgden werd het resultaat van Penrose op allerlei manieren uitgebreid. In het bijzonder paste Stephen Hawking de ideeën van Penrose toe op kosmologische metrieken, die de structuur en de evolutie van het hele universum beschrijven. Hawking toonde hiermee het bestaan van een singulariteit aan het begin van het universum aan.
Ruimtetijd in de buurt van een singulariteit
Het werk van Penrose en Hawking bewees dat singulariteiten volgens Einsteins wetten niet alleen kunnen bestaan, maar dat deze onder bepaalde aannames onvermijdelijk zijn. Wat hun resultaten niet vertellen, is hoe de ruimtetijd eruitziet in de buurt van een singulariteit. Hoe verandert de ruimtetijd van een ‘gewone ruimtetijd’ in een singulariteit, waar gangbare berekeningen ineens oneindigheden uitspuwen?
Deze vraag werd in het begin van de jaren 70 onderzocht door natuurkundigen Vladimir Belinski, Isaak Khalatnikov en Evgeny Lifschitz. In hun artikelen beargumenteren Belsinki, Khalatnikov en Lifschitz dat de metriek vlak bij een singulariteit veel veranderlijker is in de tijd, dan in de plaats: de vorm van de ruimtetijd verandert razendsnel in de tijd, maar is nagenoeg gelijk op naburige plekken. Deze bewering staat sindsdien bekend als het BKL-vermoeden. Hoewel er (nog) geen sluitend bewijs is dat het vermoeden juist is, zijn er veel onderzoeksresultaten die het vermoeden ondersteunen.
Als het BKL-vermoeden juist is, heeft dit verregaande gevolgen voor ons begrip van de ruimtetijd rondom singulariteiten. In zo’n gebied vallen de ingewikkelde vergelijkingen van Einstein dan namelijk uiteen in een verzameling van vergelijkingen die voor ieder punt afzonderlijk de evolutie van de ruimtetijd beschrijven. Hierdoor heeft de dynamiek van de ruimtetijd in één punt nauwelijks nog gevolgen voor de ruimtetijd in omliggende punten. Het zo “uiteenvallen” van de Einsteinvergelijkingen maakt het makkelijker om oplossingen te vinden die de ruimtetijd dicht bij een singulariteit beschrijven.
Kasnertijdperken
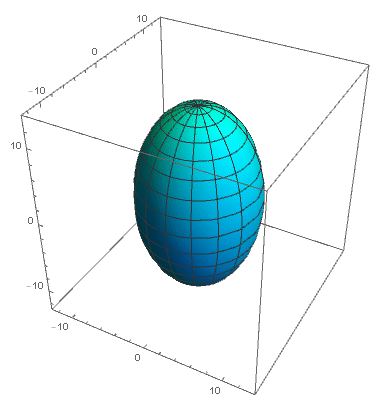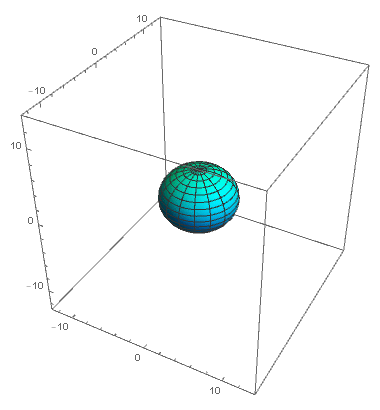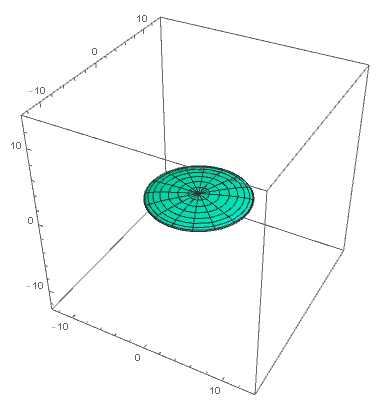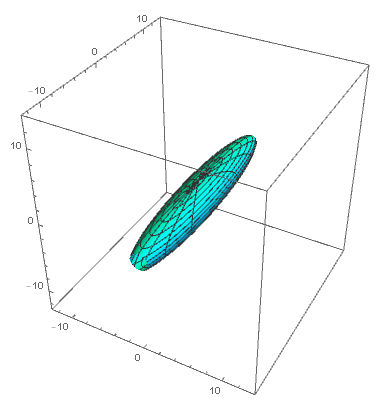
De eenvoudigste oplossing die aan het BKL-vermoeden voldoet, is gebaseerd op de Kasnermetriek. De Kasnermetriek is een oplossing van de Einsteinvergelijkingen die in 1921 door wiskundige Edward Kasner werd gepubliceerd. De metriek beschrijft een universum dat in sommige richtingen uitdijt, maar in andere richtingen inkrimpt. Dit bijzondere gedrag komt niet overeen met observaties van onze kosmos, en de Kasnermetriek lijkt dan ook geen goede beschrijving van het volledige universum te geven. Toch blijkt de Kasnermetriek een belangrijke bouwsteen te zijn om het gedrag van de ruimtetijd rondom singulariteiten te beschrijven.
Uit het werk van Belsinki, Khalatnikov en Lifschitz volgt dat de evolutie van de ruimtetijd in de buurt van een singulariteit in verschillende fasen verloopt. In elk van die fasen wordt de vorm van de ruimtetijd op ieder punt goed benaderd door een beschrijving aan de hand van een Kasnermetriek. Aan het eind van zo’n Kasnertijdperk verandert de Kasnermetriek plotseling: richtingen die eerst uitdijden, krimpen nu in en vice versa. Zo ontstaat een schommeling waarin uitdijingen en inkrimpingen elkaar voortdurend afwisselen. Hoe dichter een punt bij de singulariteit ligt, hoe sneller de Kasnertijdperken elkaar opvolgen.
De metriek als biljartbal
Om grip te krijgen op dit abstracte verhaal, introduceerde Charles Misner1 in 1994 een nuttige analogie: het kosmologisch biljart. Hij liet zien dat delen van de metriek geïnterpreteerd kunnen worden als biljartballen in een chaotisch biljart. De ‘biljarttafel’ wordt in deze analogie gevormd door een abstracte ruimte van metriekparameters. Tijdens een Kasnertijdperk beweegt de metriekbiljartbal zich in een rechte lijn over het biljart. Zodra de bal de rand van het biljart bereikt, vindt een sterke verandering van richting plaats, die overeenkomt met de overgang naar een volgend Kasnertijdperk.
Of dit biljartspel zich daadwerkelijk afspeelt in ons universum, is onduidelijk. Aangezien het hier om natuurkunde in een minuscuul klein gebied gaat, wordt er verwacht dat er een theorie van quantumzwaartekracht nodig is om de ruimtetijd rondom een singulariteit écht te begrijpen. Zo’n theorie combineert de relativiteitstheorie met de quantummechanica – de theorie van natuurkunde op de allerkleinste schaal. Mogelijk zou het kosmologisch biljart dan plaatsmaken voor een quantum-kosmologisch biljart, maar zonder theorie van quantumzwaartekracht is het onmogelijk om dat met zekerheid te zeggen. Hoe dan ook geeft het kosmologisch biljart een verassend intuïtief beeld in een verder abstract verhaal.
[1] Het werk van Misner was grotendeels gebaseerd op ongepubliceerde resultaten uit het proefschrift van Prakash Chitre uit 1972.